ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ГАЗЕ

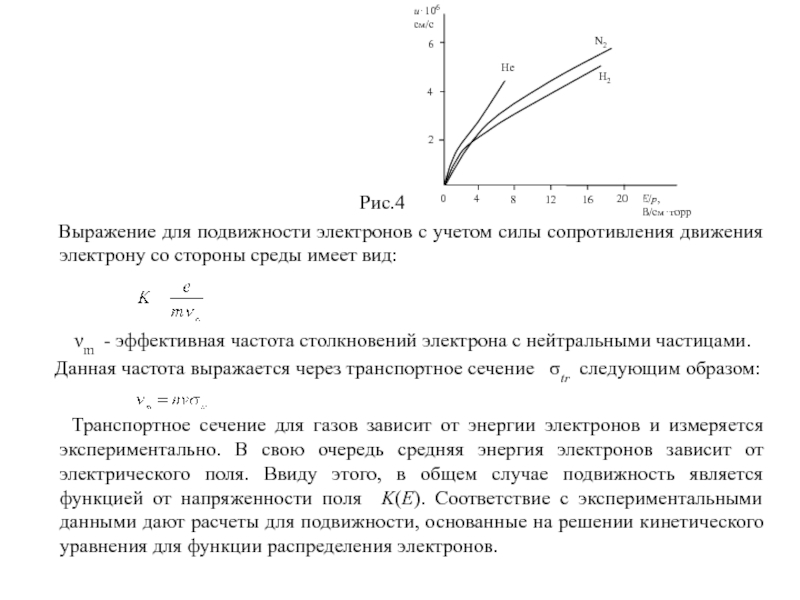
Ввиду рассмотрения тока

в слабоионизованном газе (α<<1) или в низкотемпературной плазме, требуется определить основные величины, связанные с подвижностью электронов и ионов. Существует ряд экспериментов, в которых были найдены значения подвижностей заряженных частиц для различных газов. Первой теорией подвижности ионов явилась созданная в начале XX века теория Ланжевена, получившая основные закономерности, подтверждаемые экспериментально.
Рассмотрим дрейфовое движение ионов (рис.1). Предположим, что энергия, теряемая при любом упругом или неупругом столкновении иона и атома определяется следующим неравенством:

при одном столкновении
eEx – энергия, которую

набирает ион в направлении электрического поля,
x – смещение в направлении электрического поля


Рис.1


Допустим, что существует превышение количества упругих столкновений над количеством неупругих. Для стационарного режима движения данные энергии по порядку равны:

Скорость дрейфа ионов определяется в виде:


Коэффициентом пропорциональности является величина K –подвижность ионов, т.е. скорость движения по направлению силовой линии электрического поля при Е= 1 В/м.

в середине XX века были предложены различные экспериментальные методы. Рассмотрим

наиболее известные эксперименты. На рис.2 представлен “метод запирающих сеток”.




Рис.2

На электроды В и С , расположенные в камере с пониженным газовым давлением подается постоянное напряжение U. Считается, что в данном пространстве существует низкая концентрация ионов и они движутся в направлении электрода В. На сетки 1 и 2 подается переменное синусоидальное напряжение, как показано на рис.2. В моменты, когда напряжение на данных сетках равно нулю, существуют наиболее благоприятные условия для прохождения ионов.

величины напряжения на сетках. Условие прохождения ионов может быть записано

в виде:

n =1, 2, 3…

Из данной формулы находится дрейфовая скорость, а затем рассчитывается подвижность ионов К.
В качестве другого метода определения подвижности рассмотрим эксперимент Хорнбека (рис.3). В камере установлены электроды, один из которых сетчатый. Параметры установки были следующие: расстояние между электродами d=1 см, давление в камере p=0,1-30 торр, ток I~0,1 мкА, E/p~10-103 В/см⋅торр.




Рис.3

аргон, ксенон, криптон. Межэлектродное пространство (1) облучалось УФ-излучением с помощью

искры (2). Часть излучения направлялось на фотодиод (5). После вспышки искры в пространстве (1) возникает таунсендовский лавинный разряд и на аноде за время te ~0,1 мкс собираются электроны, а на катоде – ионы за время ti =2-20 мкс. Данные импульсы регистрировались на осциллографе. Полученные результаты для подвижностей ионов нашли хорошее соответствие с теорией Ланжевена. Представим значения подвижностей для ионов неона в газообразном неоне при Т=300 К и n=2,7⋅1019 см-3, полученные в данных экспериментах и найденные из теории Ланжевена:
Кэксп≈4,4 см2/В⋅с, Ктеор≈6,7 см2/В⋅с

разработанную известным французским ученым Полем Ланжевеном в 1903-05 г. В

первой теории (1903 г.) Ланжевен исходил из следующих предположений.
1) Ионы и электроны представляют собой непроницаемые упругие шары, поэтому считается, что взаимодействие происходит только в момент столкновения.
2) Выполняются следующие неравенства:

( )

Энергия, набранная ионом в электрическом поле, значительно меньше его средней кинетической энергии.
3) Плотность ионов ni мала и взаимодействиями ионов друг с другом можно пренебречь.

между двумя столкновениями иона с нейтральными атомами (рис.1). Данные длины

x статистически распределены около λ - средней длины свободного пробега одинаковой для ионов и молекул. Считается, что в результате столкновения ион полностью теряет свою скорость. Время между двумя столкновениями определяется в виде . Расстояние, пройденное ионом при ускорении в электрическом поле выражается в виде:



Для вычисления среднего значения требуется усреднить величину x2 с помощью распределения, учитывающего длину свободного пробега λ .



Где -макроскопическое эффективное сечение ионно-молекулярного упругого рассеяния. С учетом данных выражений величина выразится следующим образом:

В результате формула для подвижности ионов будет иметь

вид:


С учетом выражения для длины свободного пробега и среднеквадратичной скорости подвижность имеет следующие основные зависимости:


Формула правильно выражает зависимость от концентрации n, подтверждаемую экспериментально, но для зависимости от температуры T соответствия найдено не было.
Впоследствии данная формула для подвижности ионов была уточнена Ланжевеном для распределения скоростей и отличия масс иона m и молекулы M.

vкв - среднеквадратичная скорость молекул,

D12 – сумма радиусов молекулы и иона,
n - концентрация молекул
Данный вариант формулы лучше соответствовал экспериментальным данным, но все же не учитывал взаимодействие ионов и молекул.

Ввиду этого, в 1905 г. Ланжевеном была создана теория, учитывающая взаимодействие ионов и молекул. Предполагалось, что в результате взаимодействия иона и молекулы происходит поляризация молекулы и у молекулы появляется дипольный момент d ≠ 0. Тогда сила притяжения иона и молекулы будет выражаться в виде:


ε - диэлектрическая проницаемость газа, e – заряд иона, n – концентрация молекул

подвижности приобретает вид:


ρ -плотность газа, ε -

диэлектрическая проницаемость газа,
M – масса молекулы, m - масса иона
A(a) – функция Ассе, при а=0,5-4,0 ; А=0,51-0,18


p – давление газа, D12 – сумма радиуса иона и молекулы
Окончательный вариант подвижности ионов в теории Ланжевена нашел наилучшее соответствие с экспериментальными данными.
Теоретическое представление выражения для подвижности электронов осложняется тем, что зависимость дрейфовой скорости от напряженности электрического поля не является линейной.
На рис.4 изображены зависимости дрейфовой скорости u от отношения E/p для некоторых газов. Поэтому данные кривые можно аппроксимировать обычной зависимостью только на линейных участках:

Рис.4
Выражение для подвижности электронов с учетом силы сопротивления движения электрону со стороны среды имеет вид:


νm - эффективная частота столкновений электрона с нейтральными частицами.
Данная частота выражается через транспортное сечение σtr следующим образом:

Транспортное сечение для газов зависит от энергии электронов и измеряется экспериментально. В свою очередь средняя энергия электронов зависит от электрического поля. Ввиду этого, в общем случае подвижность является функцией от напряженности поля K(E). Соответствие с экспериментальными данными дают расчеты для подвижности, основанные на решении кинетического уравнения для функции распределения электронов.