Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ по математике 2012
Содержание
- 1. ЕГЭ по математике 2012
- 2. План встречиЗнакомство.Анализ результатов ЕГЭ 2011 года.Особенности варианта
- 3. Особенности варианта 2012Добавлено 2 задачи в часть
- 4. Структура варианта 2011 года12 задач группы В
- 5. Структура варианта 2011 годаЗадачи по алгебре -
- 6. Анализ результатов 2011 годаНизкий уровень подготовки (не
- 7. Сравнение результатов 2010 и 2011 годов Во
- 8. Низкий уровень подготовки (до 5 баллов)Основной вклад
- 9. Национальная катастрофа с задачей В1В доме, в
- 10. Базовый уровень подготовки. Резервы.В4 «найти угол» -
- 11. Особенности выполнения задач группы СВ задаче С1
- 12. Задача С3Сделали верный переход от логарифмического неравенства
- 13. Задача С 3.Вывод: свойства логарифмов сильными учениками
- 14. Вариант ЕГЭ 2012В целом близок в варианту 2011.Что изменено и почему?
- 15. Две новые задачи части В.
- 16. Примеры задач В10.В соревнованиях по толканию ядра
- 17. Примеры задач В 10.На экзамене по геометрии
- 18. Новая задача В 9.Диагональ основания правильной четырёхугольной
- 19. «Графическая» задача на производную В 8. В скольких точках из отмеченных производная отрицательна?
- 20. Изменения в части С.Задача С1 явно с
- 21. С1 из демоверсии 2012Решите уравнение и найдите корни, принадлежащие отрезку
- 22. Задача С3 - 2012Система двух показательно- логарифмических
- 23. Задача С3 – демоверсия 2012
- 24. Как готовить класс к ЕГЭ? Методические и психологические соображения.
- 25. «Лозунг»Со слабыми учениками работать над их сильными
- 26. Психологические особенности подготовки к ЕГЭ. Личное мнение
- 27. Психологические особенности подготовки к ЕГЭ. Личное мнение
- 28. Формы работы на уроке.Устный счетМатематические диктантыПоэлементная отработка (решение части задачи).
- 29. Задача С1.1) Считать «картинку» необходимой частью решения тригонометрического уравнения (даже, если отбор корней не нужен).
- 30. Задача С1.Не употреблять записьЭта запись не показывает:что
- 31. Задача С1.Давать отдельные задачи на отбор корней без решения уравнений.
- 32. Задача С1.Учиться проверять ответ. Для этого задавать
- 33. Задача С1.Постараться, чтобы ученики пользовались и единичной окружностью, и графиками функций.
- 34. Задача С2.Выбрать для повторения один объект (лучше
- 35. Пример серии задач на куб.Возьмем диагональ грани.
- 36. Задача С2.Задачи с одним объектом хороши тем,
- 37. С3. О неравенствах.Учиться решать системы неравенств в
- 38. С 5. О задачах с параметром.Знакомить с
- 39. С 5. О задачах с параметром.Максимально использовать
- 40. Не переготовиться!Если слишком много готовиться к экзамену,
- 41. Печатные и электронные ресурсыШкольные учебники!!Открытый банк задач
- 42. КонтактыШноль Дмитрий Эммануиловичdshnol@mail.ru
- 43. Скачать презентанцию
План встречиЗнакомство.Анализ результатов ЕГЭ 2011 года.Особенности варианта 2012 года.О методике подготовки к ЕГЭ по математике. Общие вопросы и разбор конкретных заданий. Печатные и электронные ресурсы. Вопросы, реплики, обсуждения.
Слайды и текст этой презентации
Слайд 2План встречи
Знакомство.
Анализ результатов ЕГЭ 2011 года.
Особенности варианта 2012 года.
О методике
подготовки к ЕГЭ по математике. Общие вопросы и разбор конкретных
заданий.Печатные и электронные ресурсы.
Вопросы, реплики, обсуждения.
Слайд 3Особенности варианта 2012
Добавлено 2 задачи в часть В:
Вероятностная задача
Легкая стереометрия
Заранее
объявлен порог
положительной оценки:
5 первичных баллов.
Слайд 4Структура варианта 2011 года
12 задач группы В (по 1 баллу)
6
задач группы С:
С1 и С2 – уровень школьной «пятерки» (по
2 балла)С3 и С4 - уровень сильного технического ВУЗа (по 3 балла)
С5 и С6 – уровень ВУЗов математических специальностей (по 4 балла)
Итого: 30 первичных баллов
Слайд 5Структура варианта 2011 года
Задачи по алгебре - 6 (В3, В7,
В10, В12, С1, С3)
Функции и начала анализа - 3 (В8,
В11, С5) Задачи по геометрии - 5 (В4, В6, В9, С2, С4)
Практико-ориентированные задачи - 3 (В1, В2, В5).
Логико-комбинаторная задача – С6.
Слайд 6Анализ результатов 2011 года
Низкий уровень подготовки (не больше 5 первичных
баллов) – 16%
Базовый уровень подготовки (от 6 до 12
первичных баллов) – 58%Повышенный уровень подготовки (от 13 до 22 первичных баллов) – 25%
Высокий уровень подготовки (больше 23 первичных баллов) – 1%
Слайд 7Сравнение результатов 2010 и 2011 годов
Во всех группах сдвиг
в лучшую сторону примерно на 1 балл.
Особенное улучшение: В9 (стереометрия),
В8 (производная, касательная), С3 (логарифмическое неравенство).Некоторое ухудшение: В7 (тригонометрия вместо логарифмов в 2010)
Слайд 8Низкий уровень подготовки (до 5 баллов)
Основной вклад –
практико-ориентированные
задачи
В2, В5, В1
простейшее уравнение - В3
и геометрия
на клетчатой доске – В6.
Слайд 9Национальная катастрофа с задачей В1
В доме, в котором живет Петя
один подъезд. На каждом этаже по шесть квартир. Петя живет
в квартире 45. На каком этаже живет Петя?20% неверных ответов!!!
Слайд 10Базовый уровень подготовки. Резервы.
В4 «найти угол» - не сделали 20%
группы.
В1 не сделали 17% группы!!!
В7 - найти значение тригонометрической функции
– сделали меньше половины.В11 - производная на отрезке сделали 44 %
Слайд 11Особенности выполнения задач группы С
В задаче С1 верно решили тригонометрическое
уравнение – 42%,
а верно отобрали корни 20%.
Слайд 12Задача С3
Сделали верный переход от логарифмического неравенства к системе неравенств
– 11%
Верно решили полученную систему неравенств – 4 %.
Слайд 13Задача С 3.
Вывод: свойства логарифмов сильными учениками усвоены прилично,
а
умения грамотно работать с системами неравенств недостаточны.
Слайд 15Две новые задачи части В.
Задача на
вероятность (В10).
В сборнике билетов по биологии всего 25 билетов,
в двух из них встречается вопрос о грибах. На экзамене школьнику достается один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.Слайд 16Примеры задач В10.
В соревнованиях по толканию ядра участвуют 4
спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из
Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Швеции.Слайд 17Примеры задач В 10.
На экзамене по геометрии школьнику достается одна
задача из сборника. Вероятность того, что эта задача на тему
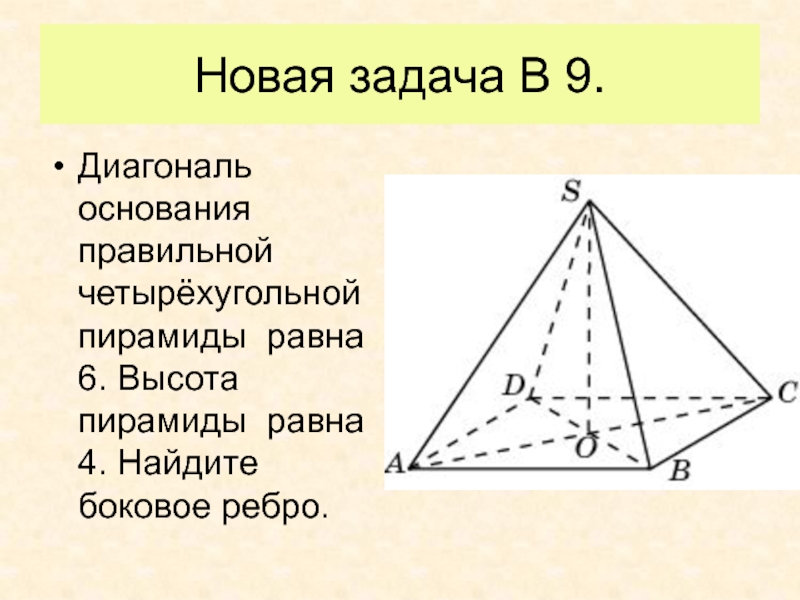
«Вписанная окружность», равна 0,2. Вероятность того, что это окажется задача на тему «Параллелограмм», равна 0,15. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.Слайд 18Новая задача В 9.
Диагональ основания правильной четырёхугольной пирамиды равна 6.
Высота пирамиды равна 4. Найдите боковое ребро.
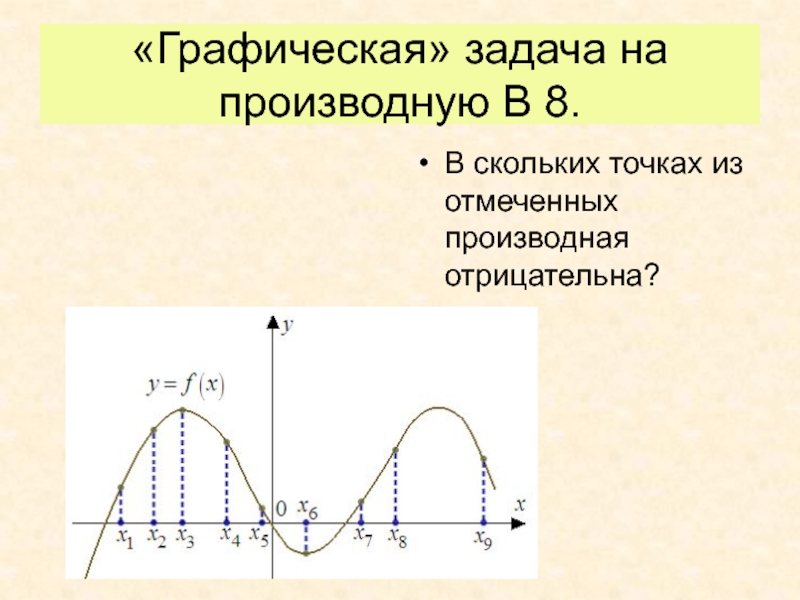
Слайд 19«Графическая» задача на производную В 8.
В скольких точках из
отмеченных производная отрицательна?
Слайд 20Изменения в части С.
Задача С1 явно с большой вероятностью будет
разделена на две части (по 1 баллу за каждую часть):
Решить
уравнение.Найти корни, удовлетворяющие данному условию.
Слайд 22Задача С3 - 2012
Система двух показательно- логарифмических неравенств.
Более четко
выделяются критерии проверки:
Решение каждого из неравенств
по 1 баллу,
решение
системы 3 балла. Слайд 25«Лозунг»
Со слабыми учениками работать над их сильными сторонами.
С сильными учениками
работать над их слабыми сторонами.
У средних учеников постоянно поддерживать их
сильную сторону и выделять ту часть из плохо усвоенного, которую реально сделать за оставшееся время.Слайд 26Психологические особенности подготовки к ЕГЭ. Личное мнение лектора.
17-летние юноши и
девушки - давно не дети и многое могут и должны
делать сами:Определить цели при сдаче ЕГЭ (получить зачет, поступить в технический вуз или на математическую специальность).
Определить в начале учебного года собственный уровень подготовки и сформулировать свой план подготовки к ЕГЭ.
Находить пособия и сайты, которые им помогут.
Слайд 27Психологические особенности подготовки к ЕГЭ. Личное мнение лектора.
Учитель помогает молодым
людям подготовиться к ЕГЭ, но не берет всю ответственность на
себя (даже, если эту ответственность на него возлагает начальство).Молодым людям крайне не полезно быть в роли детей, за которых кто-то взрослый отвечает. Тогда они расслабляются и ничего не хотят.
Слайд 28Формы работы на уроке.
Устный счет
Математические диктанты
Поэлементная отработка (решение части задачи).
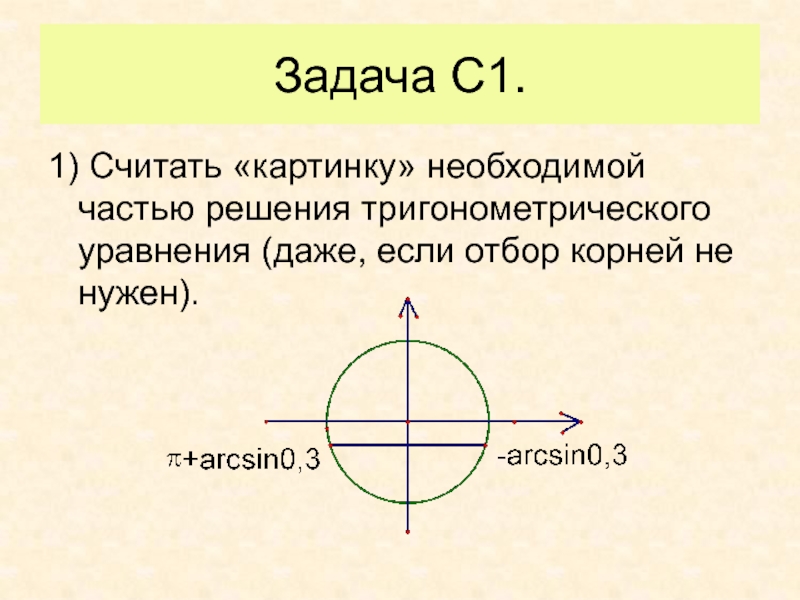
Слайд 29Задача С1.
1) Считать «картинку» необходимой частью решения тригонометрического уравнения (даже,
если отбор корней не нужен).
Слайд 30Задача С1.
Не употреблять запись
Эта запись не показывает:
что серий решений две
Что
период синуса 2П.
Отбирать корни при такой форме записи крайне
неудобно.Слайд 32Задача С1.
Учиться проверять ответ. Для этого задавать вопрос: сколько корней
данная серия решений может иметь на данном отрезке.
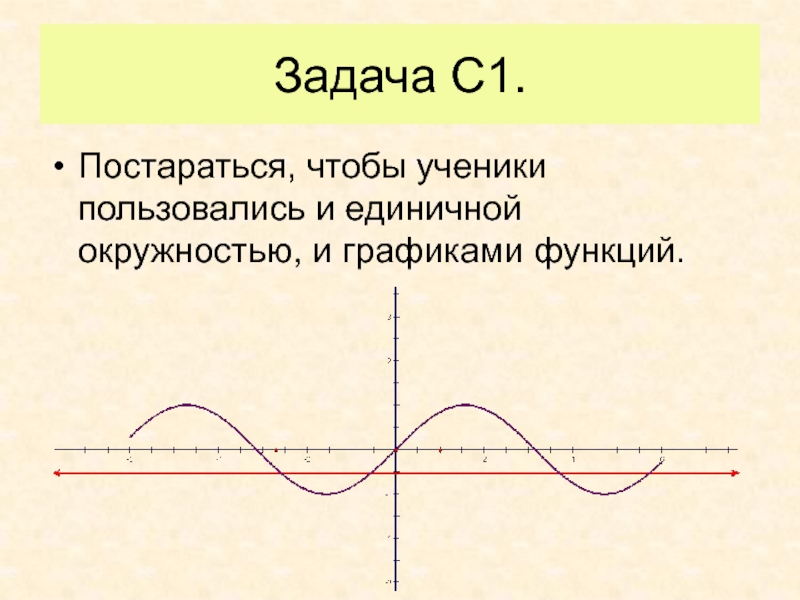
Слайд 33Задача С1.
Постараться, чтобы ученики пользовались и единичной окружностью, и графиками
функций.
Слайд 34Задача С2.
Выбрать для повторения один объект (лучше всего куб) и
на нем найти все, что можно. Тем самым решить несколько
десятков задач на одну конструкцию.Начинать с совсем устных задач, и шаг за шагом усложнять.
Слайд 35Пример серии задач на куб.
Возьмем диагональ грани. И найдем:
Углы со
всеми прямыми (ребрами, диагоналями граней, диагоналями),
Углы со всеми плоскостями (гранями
и сечениями, проходящими через 3 вершины)Расстояния от выбранной диагонали до всех скрещивающихся прямых.
Слайд 36Задача С2.
Задачи с одним объектом хороши тем, что сильные могут
идти вперед, придумывая себе все более сложные задачи.
Удобно работать на
готовых чертежах, чтобы не тратить время урока на построение. Слайд 37С3. О неравенствах.
Учиться решать системы неравенств в 10 или 11
классе – поздно.
Естественное время для систем неравенств – первое полугодие
9 класса. На чем можно сэкономить время?
Слайд 38С 5. О задачах с параметром.
Знакомить с идейной стороной задач
с параметром нужно как можно раньше, самое лучшее с 7
класса. Пример задачи:Исследуйте в каких четвертях в зависимости от b может располагаться точка пересечения графиков функций у=2х-6 и у=х+b.
Слайд 39С 5. О задачах с параметром.
Максимально использовать геометрический язык.
при
изменении параметра…
…прямая двигается вдоль оси У
… вращается вокруг точки…
…центр окружность
двигается по прямой…… изменяется величина угла (модуль) и.т.д.
Слайд 40Не переготовиться!
Если слишком много готовиться к экзамену, в частности, слишком
часто писать пробные варианты, то есть опасность только ухудшить результаты.
Как
говорят музыканты, нужно «не заиграть руку». Навык, доведенный до полного автоматизма, начинает неожиданно давать сбои (слишком скучно). Лучше недо-, чем пере-