Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономический рост
Содержание
- 1. Экономический рост
- 2. Вопросы лекцииЭкономический рост: сущность, типы, показатели, факторыКейнсианские
- 3. Измерение экономического роста- абсолютный прирост реального объема
- 4. Модель экономического роста Е. Домара (конец
- 5. В модели представлен только рынок благ, который
- 6. Модель экономического роста Е. ДомараПроизводственная функция В.
- 7. Модель экономического роста Е. Домара (конец 1940-х гг.)Прирост капитала обеспечивается соответствующим объемом инвестиций:
- 8. Модель экономического роста Е. ДомараПрирост инвестиций
- 9. Модель экономического роста Е. ДомараПрирост инвестиций
- 10. Модель экономического роста Е. ДомараУсловие равновесного
- 11. Существует равновесный темп прироста реального дохода в
- 12. Е. Домар пришел к выводу, что для
- 13. Модель специального экономического роста Р. Харрода (1939
- 14. Предпосылки модели специального экономического роста Р. Харрода1)
- 15. Модель специального экономического роста Р. Харрода (1939
- 16. Модель специального экономического роста Р. Харрода (1939
- 17. Модель специального экономического роста Р. Харрода (1939
- 18. Модель специального экономического роста Р. Харрода (1939
- 19. Модель специального экономического роста Р. Харрода (1939 г.)Равновесный экономический рост предполагает равенство спроса и предложения:
- 20. Модель специального экономического роста Р. Харрода (1939 г.)После преобразования получим:
- 21. Модель специального экономического роста Р. Харрода (1939
- 22. Модель специального экономического роста Р. Харрода (1939 г.)Тогда предыдущее выражение будет иметь вид:
- 23. Модель специального экономического роста Р. Харрода (1939
- 24. Модель специального экономического роста Р. Харрода (1939
- 25. Модель специального экономического роста Р. Харрода (1939
- 26. Особенности неоклассических моделей экономического ростаИмеют дело с
- 27. Неоклассическая модель экономического роста Р. Солоу (1956
- 28. Предпосылки модели Р. СолоуФакторы производства являются взаимозаменяемыми.Цены
- 29. Неоклассическая модель экономического роста Р. Солоу Объем
- 30. Модель экономического роста Р. СолоуПроизводственная функция Кобба-ДугласаKLq1q2q3Изокванты
- 31. Производственная функция Кобба-ДугласаМодель экономического роста Р. Солоу
- 32. Неоклассическая модель экономического роста Р. Солоу Если
- 33. Производственная функция (в расчете на одного работника)ykf(k)sf(k)ciyMPKТангенс
- 34. Неоклассическая модель экономического роста Р. Солоу Объем
- 35. Неоклассическая модель экономического роста Р. Солоу Доход
- 36. Стационарное равновесие в модели экономического роста Р.
- 37. Стационарное равновесие в модели экономического роста Р.
- 38. Определение устойчивого уровня капиталовооруженностиyky=f(k)sf(k) (n+)kкапиталовооруженностьвыпуск на одного
- 39. Выводы: модель Р. Солоу показывает, что норма
- 40. Модель Р. Солоу с учетом технического прогрессаВключение
- 41. Модель Р. Солоу с учетом технического прогрессаЕсли
- 42. y’k’y=f(k’)sf(k’) (n++g)k’капитал на эффективную единицу трудавыпуск на
- 43. Модель Р. Солоу с учетом технического прогрессаВывод:
- 44. «Золотое правило» Э. ФелпсаМодель Р. Солоу помогает
- 45. ykf(k) (δ)kk**с**k** - устойчивый уровень фондовооруженности, соответствующий
- 46. Спасибо за внимание!
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Вопросы лекции
Экономический рост: сущность, типы, показатели, факторы
Кейнсианские модели экономического роста
Неоклассическая
модель экономического роста Р. Солоу
Слайд 3Измерение экономического роста
- абсолютный прирост реального объема выпуска
- темп роста
реального объема выпуска
- темп прироста реального объема выпуска
Слайд 4Модель экономического роста
Е. Домара (конец 1940-х гг.)
Е.Домар поставил вопрос:
если инвестиции увеличивают производственные мощности, а также создают дополнительные доходы,
то:как должны расти инвестиции, чтобы темп прироста дохода равнялся темпу прироста производственных мощностей?
Слайд 5В модели представлен только рынок благ, который сбалансирован.
Технология производства представлена
производственной функцией В. Леонтьева (факторы производства K и L невзаимозаменяемы).
На
рынке труда существует избыточное предложение, вызванное негибкостью цен.Отсутствует выбытие капитала.
Средняя производительность капитала (Y/K) и норма сбережений s стабильны.
Выпуск зависит только от одного ресурса – капитала (K).
Предпосылки модели
экономического роста Е. Домара
Слайд 6Модель экономического роста Е. Домара
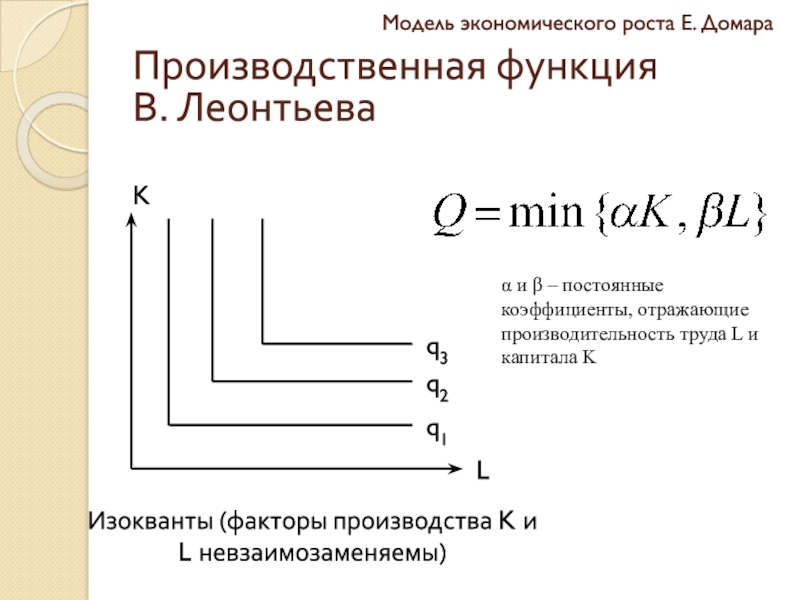
Производственная функция
В. Леонтьева
K
L
q1
q2
q3
Изокванты (факторы производства
K и L невзаимозаменяемы)
α и β – постоянные коэффициенты, отражающие
производительность труда L и капитала KСлайд 7Модель экономического роста
Е. Домара (конец 1940-х гг.)
Прирост капитала обеспечивается
соответствующим объемом инвестиций:
Слайд 8Модель экономического роста
Е. Домара
Прирост инвестиций ΔI вызовет увеличение совокупного
спроса AD:
m – мультипликатор расходов;
b – предельная склонность к потреблению;
s
– предельная склонность к сбережению.Слайд 9Модель экономического роста
Е. Домара
Прирост инвестиций ΔI вызовет также увеличение
совокупного предложения AS:
α – предельная производительность капитала.
Слайд 10Модель экономического роста
Е. Домара
Условие равновесного роста – равенство прироста
спроса и предложения:
=>После преобразования:
Темп прироста инвестиций должен быть равен произведению предельной производительности капитала и предельной склонности к сбережению
Слайд 11Существует равновесный темп прироста реального дохода в экономике, при котором
полностью используются имеющиеся производственные мощности. Он прямо пропорционален норме сбережений
и предельной производительности капитала.В соответствии с предпосылками модели предельная производительность капитала α = const, => увеличить темп прироста инвестиций может лишь рост нормы сбережений s. Однако в рассматриваемом периоде s=const.
Поскольку в условиях равновесия I=S, a S=sY при s=const, уровень дохода пропорционален уровню инвестиций:
Инвестиции и доход растут с одинаковым постоянным во времени темпом.
Модель экономического роста Е. Домара
Слайд 12Е. Домар пришел к выводу, что для поддержания полной занятости
годовой темп роста производственных мощностей должен быть равен годовому темпу
экономического роста.Его вывод для экономической политики: только постоянный рост инвестиций обеспечивает динамическое равновесие между совокупным спросом и совокупным предложением.
Для этого государство должно влиять:
на норму накопления в национальном доходе (ее рост повлечет рост предельной склонности к сбережению),
на темпы технического прогресса (определяют рост производительности капитала).
Модель экономического роста
Е. Домара
Слайд 13Модель специального экономического роста Р. Харрода (1939 г.)
Модель Харрода
исследует траекторию роста экономики.
Особое внимание в модели уделяется темпу,
с которым должен расти национальный доход (Y), чтобы удовлетворить условию кейнсианской экономической теории: сбережения (St) = инвестиции (It),
Слайд 14Предпосылки модели специального экономического роста Р. Харрода
1) В модели представлен
только рынок благ.
2) Функция инвестиций является эндогенной (в модели Домара
– экзогенной).3)Величина капиталоемкости K/Y постоянна.
4) Поведение предпринимателей зависит от их ожиданий относительно спроса на товары и услуги.
Слайд 15Модель специального экономического роста Р. Харрода (1939 г.)
Любой рост (сокращение)
дохода вызывает рост (сокращение) капиталовложений, пропорциональный изменению дохода (принцип акселератора).
Акселератор показывает, во сколько раз возрастут новые инвестиции в ответ на рост объема производства (дохода, =>) совокупного спроса.
ν - акселератор
Слайд 16Модель специального экономического роста Р. Харрода (1939 г.)
Предприниматели планируют объем
производства, исходя из ситуации, сложившейся в экономике в предшествующий период:
α=1,
если в предшествующем периоде (t-1) спрос был равен предложению;α>1, если в предшествующем периоде (t-1) спрос превысил предложение;
α<1, если в предшествующем периоде (t-1) спрос был ниже предложения.
Слайд 17Модель специального экономического роста Р. Харрода (1939 г.)
Объем предложения в
экономике:
α=1, если в предшествующем периоде (t-1) спрос был равен предложению;
α>1,
если в предшествующем периоде (t-1) спрос превысил предложение;α<1, если в предшествующем периоде (t-1) спрос был ниже предложения.
Слайд 18Модель специального экономического роста Р. Харрода (1939 г.)
Объем спроса в
экономике определяется, исходя из равенств: I=S, ΔS=sΔY и модели акселератора:
Слайд 19Модель специального экономического роста Р. Харрода (1939 г.)
Равновесный экономический рост
предполагает равенство спроса и предложения:
Слайд 21Модель специального экономического роста Р. Харрода (1939 г.)
Если в предшествующем
периоде спрос был равен предложению, т.е. α = 1, то
темпы роста производства сохранятся на уровне предшествующего периода:Слайд 22Модель специального экономического роста Р. Харрода (1939 г.)
Тогда предыдущее выражение
будет иметь вид:
Слайд 23Модель специального экономического роста Р. Харрода (1939 г.)
Равновесный темп объема
выпуска составит:
- «гарантированный» темп роста (если его поддерживать, ожидания предпринимателей
будут сбываться, т.к. спрос будет равен предложению, но полная занятость будет достигаться не всегда) Слайд 24Модель специального экономического роста Р. Харрода (1939 г.)
«Естественный темп роста»
– это максимальный темп, допускаемый ростом активного населения и техническим
прогрессом (при нем достигается полная занятость экономических ресурсов: K и L).Если естественный темп роста превышает гарантированный (из-за избытка трудовых ресурсов), то экономика будет переживать «бум».
Если естественный темп меньше гарантированного, то в экономике будет наблюдаться стагнация (ситуация, при которой экономика в течение длительного периода времени остается в фазе спада или депрессии).
Слайд 25Модель специального экономического роста Р. Харрода (1939 г.)
Идеальное равновесие экономической
системы достигается при равенстве гарантированного, естественного и фактического темпов роста
в условиях полной занятости ресурсов.Если фактический темп отклоняется от гарантированного, экономическая система отклоняется от состояния равновесия, если они равны – экономическая система находится в состоянии равновесия.
Слайд 26Особенности неоклассических моделей экономического роста
Имеют дело с закономерностями роста потенциального
ВВП, не рассматривают отклонения от него фактического ВВП.
Абстрагируются от природных
факторов, считая их сравнительно постоянными.Исходят из постулата о падающей предельной производительности капитала и труда и неизменной их совместной производительности.
Слайд 27Неоклассическая модель экономического роста Р. Солоу (1956 г.)
Цель этой модели
– ответить на вопросы:
каковы факторы сбалансированного экономического роста?
какой темп
роста может позволить себе экономика при заданных параметрах экономической системы?как при этом максимизировать доход на душу населения и объем потребления?
какое влияние на темпы роста экономики оказывают рост населения, накопление капитала и технический прогресс?
Слайд 28Предпосылки модели Р. Солоу
Факторы производства являются взаимозаменяемыми.
Цены являются гибкими, т.е.
присутствует предпосылка о совершенной конкуренции на рынках факторов производства.
Убывающая предельная
производительность капитала.Постоянная норма выбытия (амортизации).
Постоянный эффект масштаба.
Капиталовооруженность k=K/L является не постоянным отношением, а меняется в зависимости от экономической конъюнктуры (вследствие совершенной конкуренции на рынках факторов производства).
Темп роста трудовых ресурсов равен темпу роста населения.
Такие переменные, как норма сбережения, норма амортизации, рост населения, технический прогресс являются экзогенно заданными.
Слайд 29Неоклассическая модель экономического роста Р. Солоу
Объем предложения на рынке
благ описывается производственной функцией Кобба-Дугласа с постоянной отдачей от масштаба:
или (01) α – коэффициент эластичности по капиталу; 1 - α – коэффициент эластичности по трудуДля любого z>0 верно:
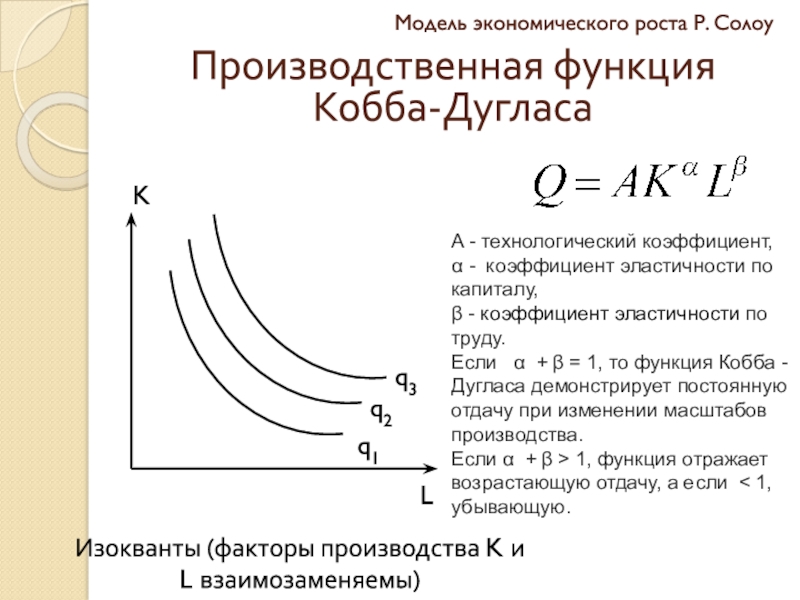
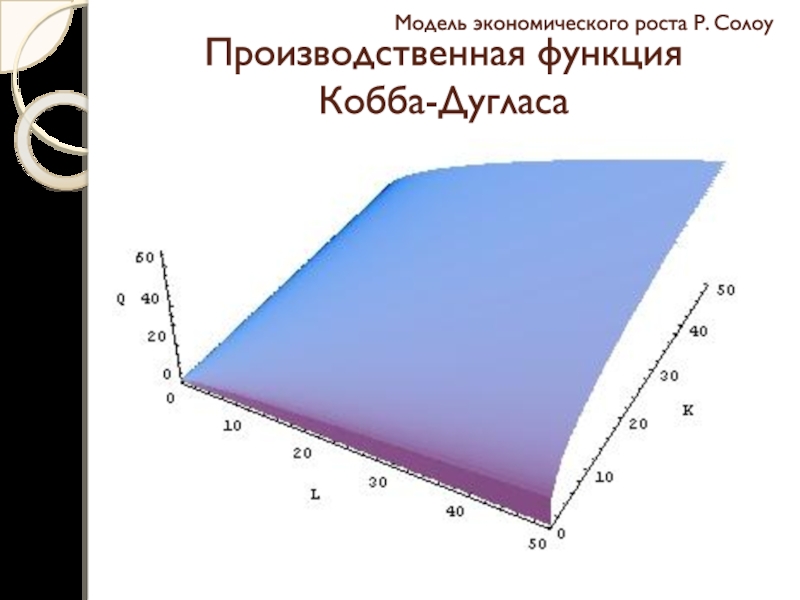
Слайд 30Модель экономического роста Р. Солоу
Производственная функция Кобба-Дугласа
K
L
q1
q2
q3
Изокванты (факторы производства K
и L взаимозаменяемы)
A - технологический коэффициент,
α - коэффициент эластичности
по капиталу, β - коэффициент эластичности по труду.
Если α + β = 1, то функция Кобба -Дугласа демонстрирует постоянную отдачу при изменении масштабов производства.
Если α + β > 1, функция отражает возрастающую отдачу, а если < 1, убывающую.
Слайд 32Неоклассическая модель экономического роста Р. Солоу
Если
, то
.Обозначим через y, a через k:
- производственная функция на одного работника
y – средняя производительность в расчете на одного работника;
k – капиталовооруженность в расчете на одного работника.
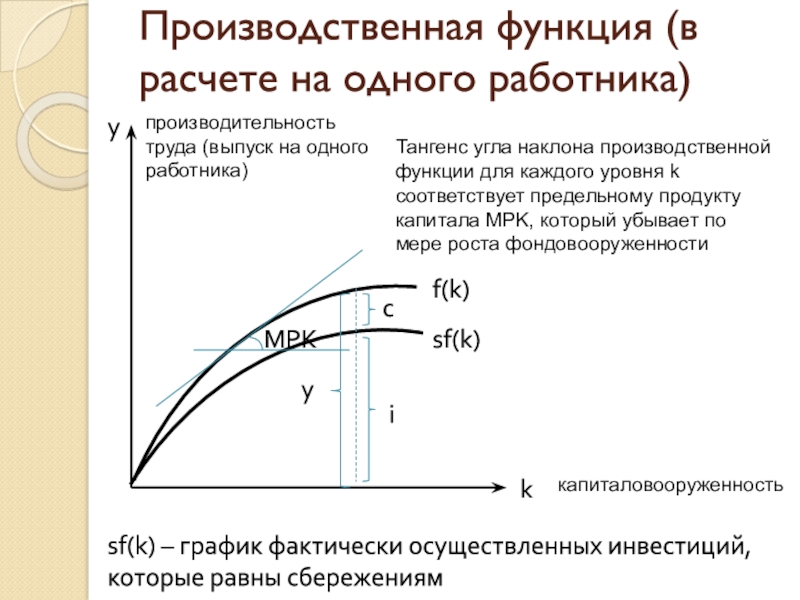
Слайд 33Производственная функция (в расчете на одного работника)
y
k
f(k)
sf(k)
c
i
y
MPK
Тангенс угла наклона производственной
функции для каждого уровня k соответствует предельному продукту капитала MPK,
который убывает по мере роста фондовооруженностикапиталовооруженность
производительность труда (выпуск на одного работника)
sf(k) – график фактически осуществленных инвестиций, которые равны сбережениям
Слайд 34Неоклассическая модель экономического роста Р. Солоу
Объем спроса на рынке
благ (без государственного заказа и чистого экспорта):
- инвестиции на одного работника
- потребление на одного работника
Слайд 35Неоклассическая модель экономического роста Р. Солоу
Доход делится между потреблением
и сбережениями в соответствии с нормой сбережения. Потребление можно представить,
как:s - норма сбережения.
Тогда:
Отсюда: (инвестиции на одного работника равны единичным сбережениям).
Слайд 36Стационарное равновесие в модели экономического роста Р. Солоу
Стационарное равновесие
- это такое состояние экономики, при котором объем капитала на
одного работника постоянен (при равенстве инвестиций и сбережений).Для того, чтобы капиталовооруженность k оставалась неизменной при условии роста населения, необходимо, чтобы капитал К увеличивался тем же темпом n, что и рост населения L.
- требуемые инвестиции в расчете на одного работника.
Если темп роста населения и темп накопления капитала равны, то выпуск на душу населения у остается неизменным.
Слайд 37Стационарное равновесие в модели экономического роста Р. Солоу
Для описания
чистого прироста капитала нужно учесть также выбытие капитала (амортизацию). Пусть
норма амортизации равна . Тогда:С учетом постоянного темпа роста населения и постоянной нормы выбытия можно в формализованном виде записать условия накопления капитала:
Когда Δk = 0, тогда производство, сбережения и требуемые инвестиции достигают определенного устойчивого уровня, т.е. экономика достигает состояния равновесия.
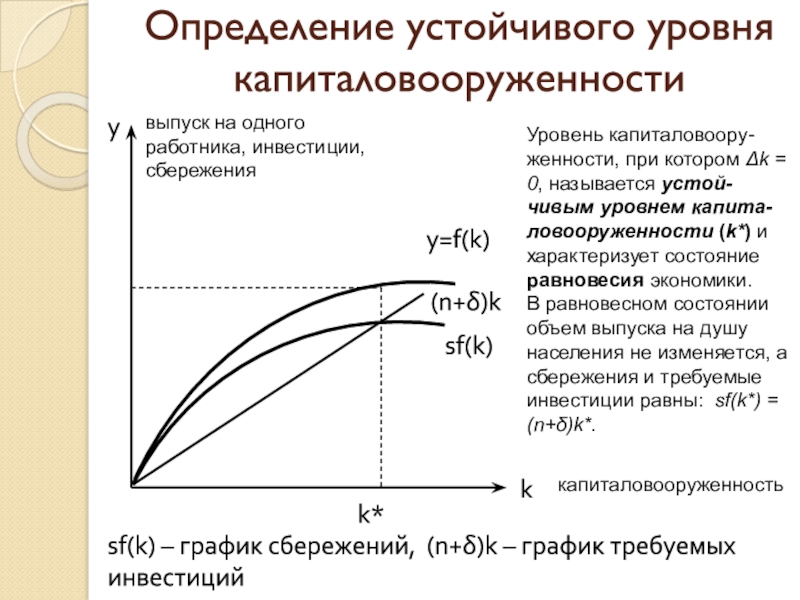
Слайд 38Определение устойчивого уровня капиталовооруженности
y
k
y=f(k)
sf(k)
(n+)k
капиталовооруженность
выпуск на одного работника, инвестиции, сбережения
sf(k)
– график сбережений, (n+)k – график требуемых инвестиций
k*
Уровень капиталовоору-женности,
при котором Δk = 0, называется устой-чивым уровнем капита-ловооруженности (k*) и характеризует состояние равновесия экономики. В равновесном состоянии объем выпуска на душу населения не изменяется, а сбережения и требуемые инвестиции равны: sf(k*) = (n+δ)k*.
Слайд 39Выводы: модель Р. Солоу показывает, что норма сбережения является важнейшим
фактором, определяющим устойчивый уровень капиталовооруженности, и, соответственно, уровень выпуска.
Чем выше
норма сбережения, тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия.Неоклассическая модель экономического роста Р. Солоу
Слайд 40Модель Р. Солоу с учетом технического прогресса
Включение в модель технического
прогресса меняет исходную производственную функцию:
T – переменная, отражающая эффективность труда
LT
– эффективный трудПример: в некоем исходном состоянии t0 в экономике занято 1000 человек. Если прирост эффективного труда LT идет темпом g, равным темпу технического прогресса 3%, то те же самые 1000 занятых произведут в следующем периоде t1продукции столько, сколько произвели бы 1030 занятых.
Слайд 41Модель Р. Солоу с учетом технического прогресса
Если определить k’ как
количество капитала в расчете на единицу труда постоянной эффективности, т.е.
, то условие равновесного состояния:sf(k’) = (n+δ+g)k’
В устойчивом состоянии k’* при наличии технического прогресса общий объем капитала K и выпуска Y будут расти с темпом (n+g). При этом с темпом g будет расти фондовооруженность k и выпуск в расчете на одного занятого y.
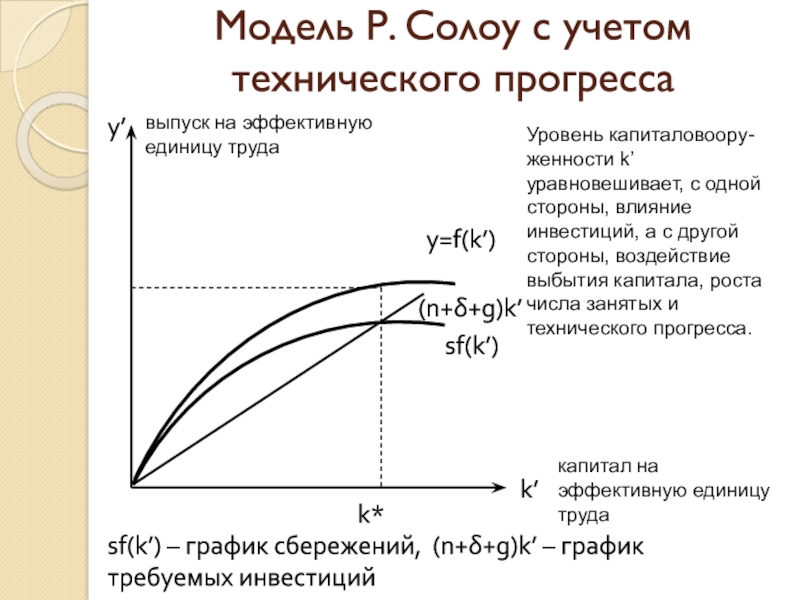
Слайд 42y’
k’
y=f(k’)
sf(k’)
(n++g)k’
капитал на эффективную единицу труда
выпуск на эффективную единицу труда
sf(k’)
– график сбережений, (n++g)k’ – график требуемых инвестиций
k*
Уровень капиталовоору-женности
k’ уравновешивает, с одной стороны, влияние инвестиций, а с другой стороны, воздействие выбытия капитала, роста числа занятых и технического прогресса.Модель Р. Солоу с учетом технического прогресса
Слайд 43Модель Р. Солоу с учетом технического прогресса
Вывод: технический прогресс является
единственным условием непрерывного роста уровня жизни, поскольку лишь при его
наличии наблюдается устойчивый рост выпуска на душу населения.Слайд 44«Золотое правило» Э. Фелпса
Модель Р. Солоу помогает определению путей максимизации
потребления при заданных темпах экономического роста.
Э. Фелпс в своем произведении
«Басня для тех, кто занимается ростом» (1961 г.) поставил вопрос: «Какая же норма сбережения максимизирует объем потребления при заданном темпе роста численности населения и неизменной технологии?»Слайд 45y
k
f(k)
(δ)k
k**
с**
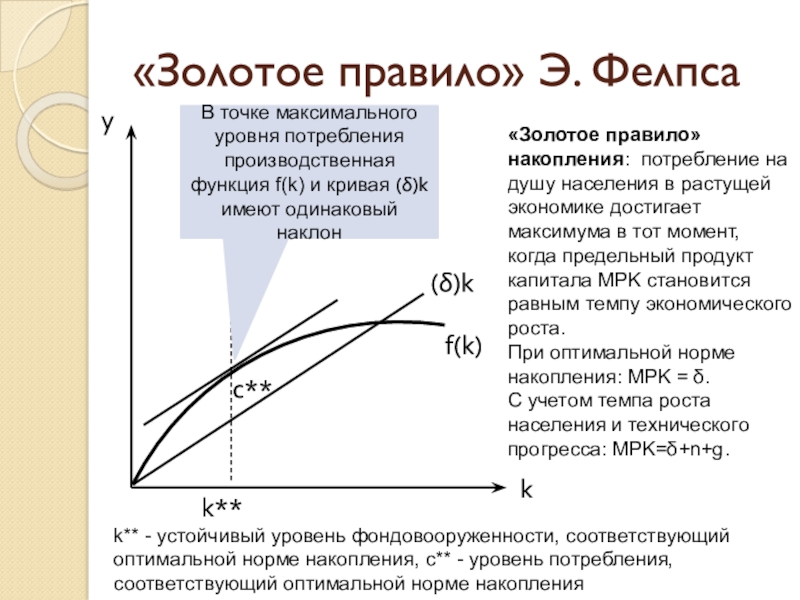
k** - устойчивый уровень фондовооруженности, соответствующий оптимальной норме накопления,
с** - уровень потребления, соответствующий оптимальной норме накопления
«Золотое правило» накопления:
потребление на душу населения в растущей экономике достигает максимума в тот момент, когда предельный продукт капитала MPK становится равным темпу экономического роста.При оптимальной норме накопления: MPK = δ.
C учетом темпа роста населения и технического прогресса: MPK=δ+n+g.
«Золотое правило» Э. Фелпса
В точке максимального уровня потребления производственная функция f(k) и кривая (δ)k
имеют одинаковый наклон