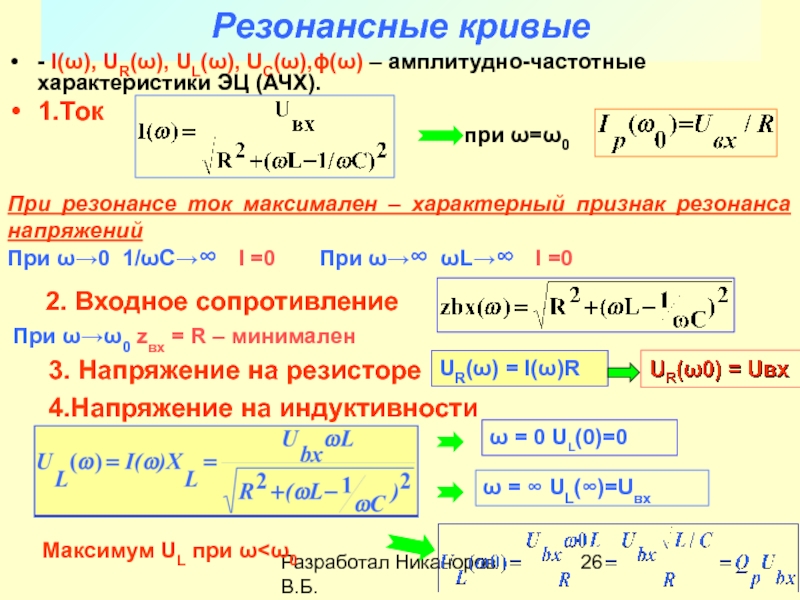
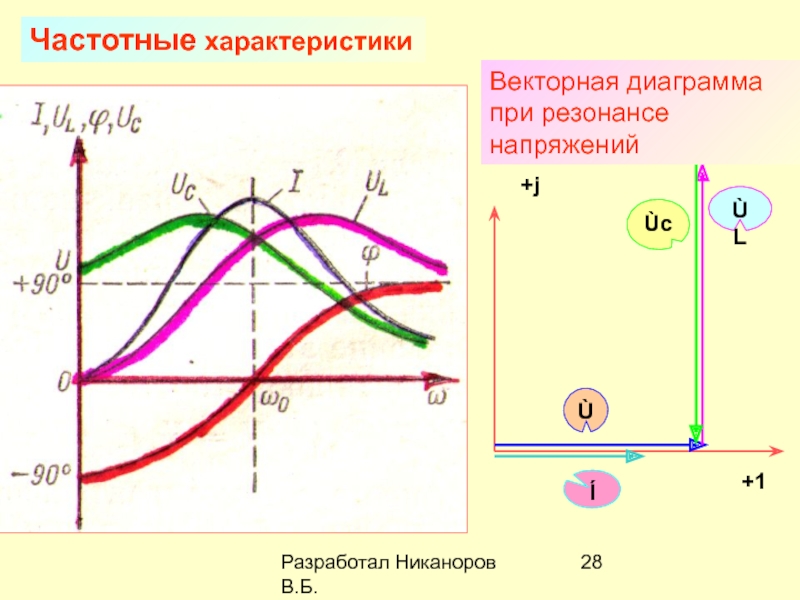
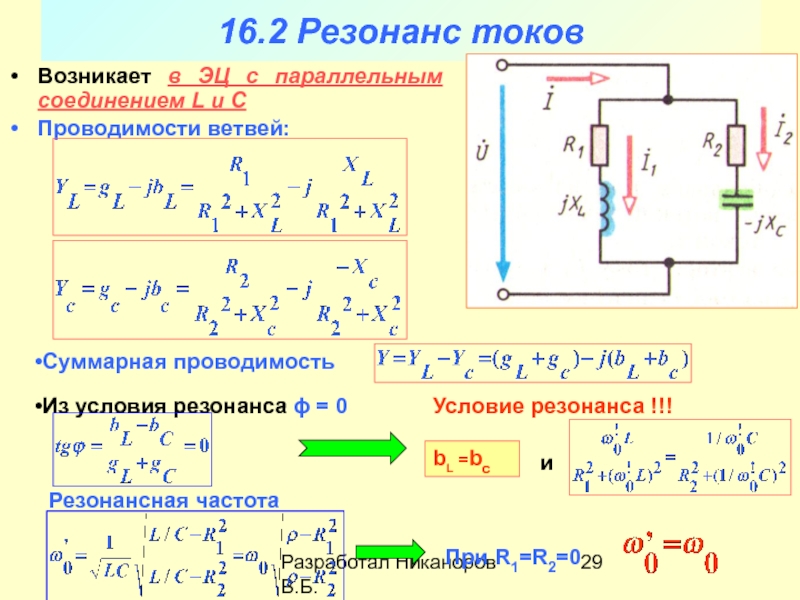
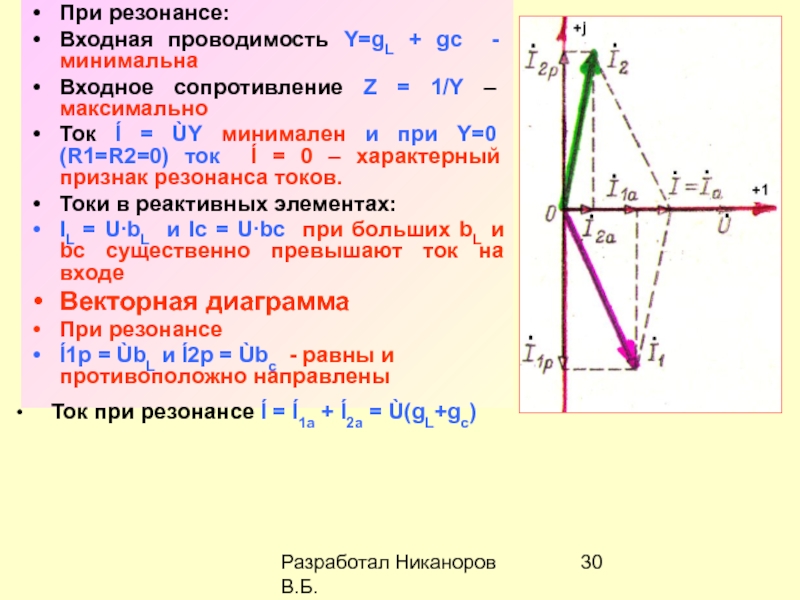
энергии в технике. Они могут быть выполнены очень большой мощности
– до 100…1500 МВт.2.Переменный ток проще трансформировать (изменять уровень), что необходимо для его экономичной передачи при высоком уровне напряжения (до 750 кВ) на большие расстояние. Трансформатор.
3. ЭТУ и электрические машины переменного тока проще и дешевле, чем ЭТУ постоянного тока.