Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электромагнитные волны
Содержание
- 1. Электромагнитные волны
- 2. Сведения из векторной алгебрыОператор наблаТогдаСкалярное произведениеВекторное произведениеУмножение вектора на числоСмешанное произведение
- 3. Максвелл, Джеймс Клерк В 1860—1865 Максвелл создал теорию
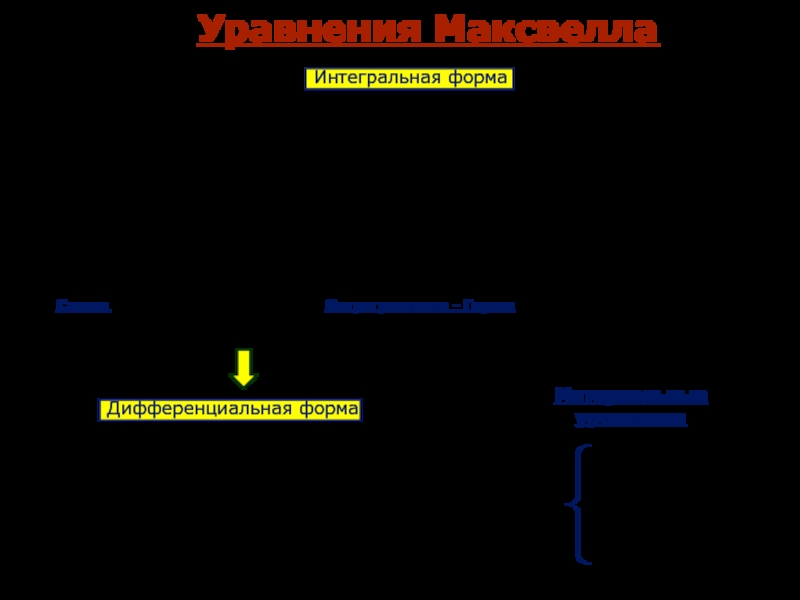
- 4. Уравнения Максвелла
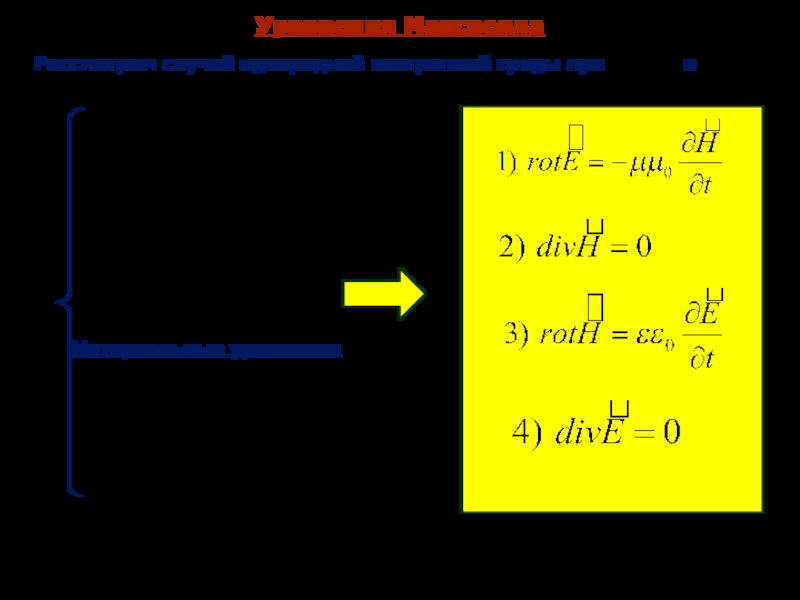
- 5. Уравнения Максвелла
- 6. Уравнения Максвелла
- 7. Рассмотрим случай плоской волны: E(z,t) т.е. Не зависит от у и х; Ур-я МаксвеллаЭлектромагнитные волны
- 8. I. Е колеблется перпендикулярно HЭлектромагнитные волны
- 9. Согласно (1)Электромагнитная волна – поперечная.Электромагнитные волныПроекция переменной
- 10. Электромагнитные волныЗадача: установить связь между E и
- 11. Электромагнитные волны
- 12. Электромагнитные волныИтак В распространяющейся ЭМВ вектора Е
- 13. Шкала ЭМВЧастотаГцДлина волны, смЭлектромагнитные волны
- 14. Видимый светЭлектромагнитные волны
- 15. Волновое уравнение ЭМВ (Даламбера)Уравнения Максвелла для плоско – поляризованной волны сводятся:Уравнение ДаламбераЭМВЭлектромагнитные волны
- 16. Электромагнитные волныСкорость ЭМВРанее для упругих колебаний было
- 17. Электромагнитные волныДля ЭМВ обозначим vсреды=Сср; vвак=C – скорость света (ЭМВ) в вакуумеВ Си
- 18. Электромагнитные волныС учётом (13) из (12):Соотношение Е и Н(14)Для амплитудных значенийДля мгновенных значений
- 19. Обобщение законов электромагнетизма. Уравнения МАКСВЕЛЛА (1867 г.)1.
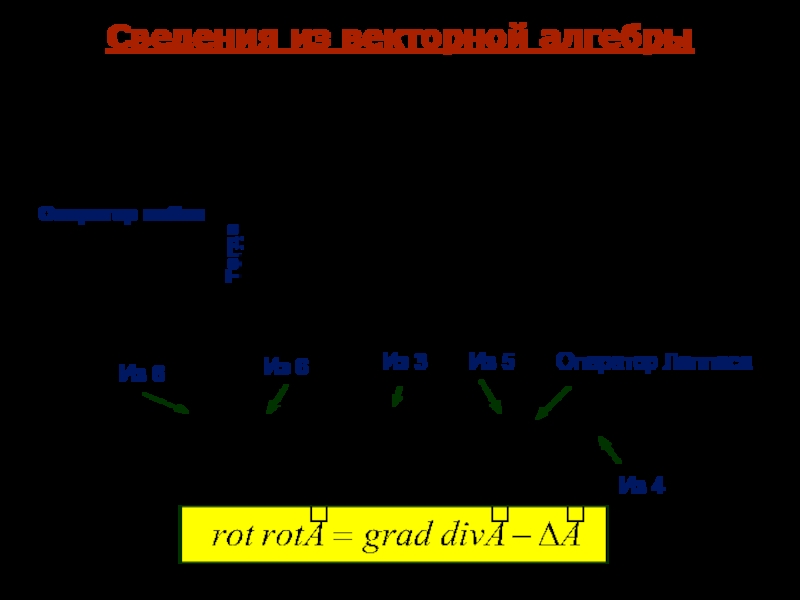
- 20. Сведения из векторной алгебрыОператор наблаТогдаИз 6Из 6Из 3Из 5Оператор ЛапласаИз 4
- 21. Электромагнитные волны
- 22. Скачать презентанцию
Сведения из векторной алгебрыОператор наблаТогдаСкалярное произведениеВекторное произведениеУмножение вектора на числоСмешанное произведение
Слайды и текст этой презентации
Слайд 2Сведения из векторной алгебры
Оператор набла
Тогда
Скалярное произведение
Векторное произведение
Умножение вектора на число
Смешанное
произведение
Слайд 3Максвелл, Джеймс Клерк
В 1860—1865 Максвелл создал теорию электромагнитного поля, которую
сформулировал в виде системы уравнений (уравнения Максвелла). Уравнения Максвелла составляют
основу как электротехники и радиотехники, так и теории любых электромагнитных явлений в любых средах.В 1861г. он обнаружил, что свет — это разновидность электромагнитных волн.
Д.К.Максвелл (1831-1879) - великий английский учёный, создатель теории электромагнетизма.
Максвелл также создал Создал кинетическую теорию газов (1859г.) и вывел соотношение для распределения частиц газов по скоростям, получившего название распределения Максвелла.
Слайд 7Рассмотрим случай плоской волны: E(z,t) т.е. Не зависит от у
и х;
Ур-я Максвелла
Электромагнитные волны
Слайд 9Согласно (1)
Электромагнитная волна – поперечная.
Электромагнитные волны
Проекция переменной составляющей магнитного и
электрического поля на ось Z (направление распространения) равна нулю.
Поперечность ЭМВ
Согласно
(2) и (3)
Слайд 10Электромагнитные волны
Задача: установить связь между E и H по фазе
и величине
Сгласно (4)
синфазность
Тождеств. вып. (12) (т.е. при любых коорд и
в любой момент)Возможно только при
В бегущей ЭМВ Е и Н колеблются в одинаковых фазах
Слайд 12Электромагнитные волны
Итак В распространяющейся ЭМВ вектора Е и Н жёстко
связаны пропорциональной зависимостью:
И колеблются в одинаковой фазе:
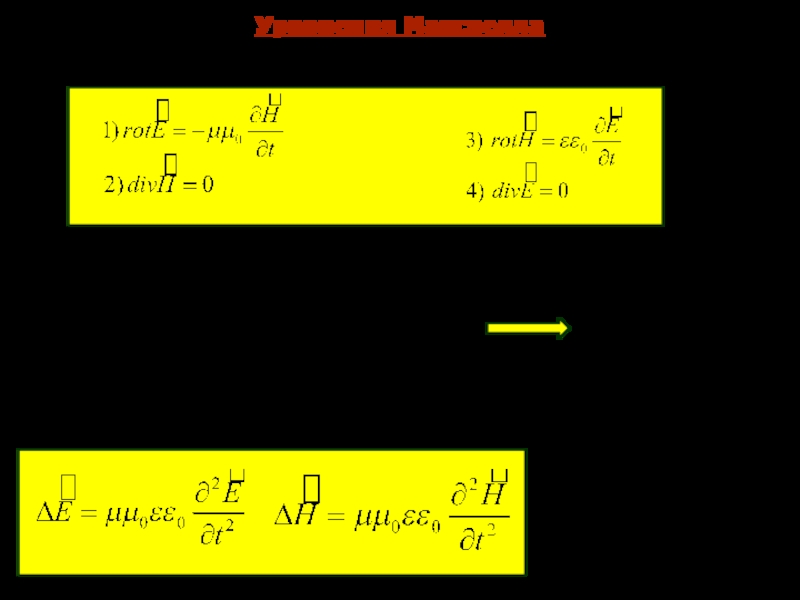
Слайд 15Волновое уравнение ЭМВ (Даламбера)
Уравнения Максвелла для плоско – поляризованной волны
сводятся:
Уравнение Даламбера
ЭМВ
Электромагнитные волны
Слайд 16Электромагнитные волны
Скорость ЭМВ
Ранее для упругих колебаний было показано:
Для бегущей волны
v – фазовая скорость.
Сравнивая (7) и (5), (6) видим:
Слайд 17Электромагнитные волны
Для ЭМВ обозначим vсреды=Сср; vвак=C – скорость света (ЭМВ)
в вакууме
В Си
Слайд 18Электромагнитные волны
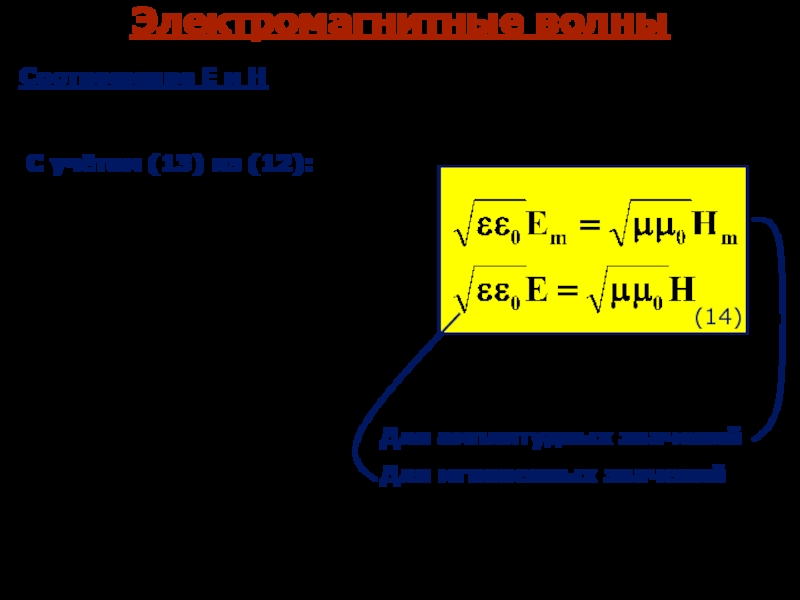
С учётом (13) из (12):
Соотношение Е и Н
(14)
Для амплитудных
значений
Для мгновенных значений
Слайд 19Обобщение законов электромагнетизма. Уравнения МАКСВЕЛЛА (1867 г.)
1. Экспериментальные законы.
I. Закон
Кулона
Теорема Гаусса
II. Закон сохранения заряда
Суммарный заряд электрически нейтральной системы остаётся
постояннымIII. Закон Ампера
Сила Лоренца (магн)
Закон Фарадея
IV. Био-Саварра-Лапласа
?
Теорема о циркуляции магн. поля
