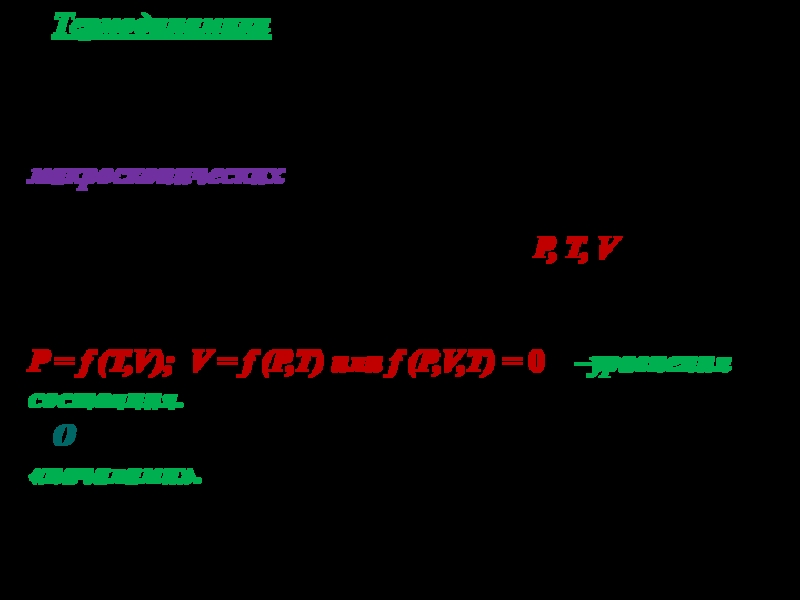Слайд 1Элементы термодинамики
Лекция № 8
Основные понятия термодинамики
1. Статистический и термодинамический методы.
2.
Основные понятия и определения молекулярной физики и термодинамики.
3. Модель идеального
газа.
4. Давление. Основное уравнение молекулярно-кинетической теории.
5. Температура и средняя кинетическая энергия теплового движения молекул.
6. Термометры. Единицы измерения температуры.
7. Уравнение Менделеева – Клайперона. Закон Авогадро.
8. Изопроцессы.
Слайд 2Статистический и термодинамический методы
Молекулярная физика и термодинамика изучают
тепловые явления. Они связаны с процессами, происходящими в макроскопических (больших)
телах, состоящих из огромного числа содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга методов: статистический (молекулярно-кинетический, отображающий микроуровень) и термодинамический (отображающий макроуровень)
Первый лежит в основе молекулярной физики, второй – термодинамики.
Слайд 3 Термодинамика возникла в 1-ой половине 19 века и
ставила своей первой задачей изучить процессы превращения тепла в механическую
работу в тепловых двигателях. Она описывает поведение макроскопических тел в тепловых процессах с помощью:
1) макроскопических параметров: P, T, V;
2) некоторых функций, связывающих эти параметры:
P = f (T,V); V = f (P,T) или f (P,V,T) = 0 –уравнения состояния.
Она базируется на законах, которые называются «началами». Они являются обобщением опытных данных. Термодинамика рассматривает теплоту как вид какого-то внутреннего движения, но не пытается конкретизировать, что это за движение.
Слайд 4 Статистическая физика (молекулярная физика) исходит из представления об
атомарно-молекулярном строении вещества и рассматривает теплоту на микроуровне как беспорядочное
движение атомов и молекул. Она вводит модели, описывающие взаимодействия отдельных частиц. Этот раздел физики называется молекулярно-кинетическая теория (МКТ).
Макроскопически наблюдаемые явления и параметры она объясняет как усредненный по огромному числу взаимодействующих частиц результат процессов, происходящих на микроуровне.
Слайд 5Основные понятия и определения молекулярной
физики и термодинамики
Совокупность тел,
составляющих макроскопическую систему, называется термодинамической системой.
Система может находиться
в различных состояниях. Величины, характеризующие состояние системы, называются макроскопическими параметрами состояния: давление P, температура T, объём V и другие (концентрация n, плотность ρ, масса m).
Связь между параметрами P, T, V специфична для каждой системы и называется уравнением состояния.
Слайд 6В строгом смысле макропараметры Р, V, Т применимы лишь к
описанию состояния термодинамического равновесия
Слайд 7 Равновесной, называется такая система, макроскопические параметры состояния которой
одинаковы во всех точках системы и не изменяются со временем
(при неизменных внешних условиях). При этом в равновесии находятся отдельные, макроскопические части системы. Говорят: система находится в термодинамическом равновесии.
Процесс – это переход из одного
равновесного состояния в другое.
Релаксация – возвращение системы
в равновесное состояние.
Время перехода – время релаксации.
Слайд 8 Если равновесие установилось, то система самопроизвольно не сможет
выйти из него.
Например, если опустить горячий камень в холодную
воду, то, через некоторое время наступит равновесное состояние: температуры выровняются. Но обратный процесс невозможен – температура камня самопроизвольно не увеличится.
Слайд 10Модель идеального газа
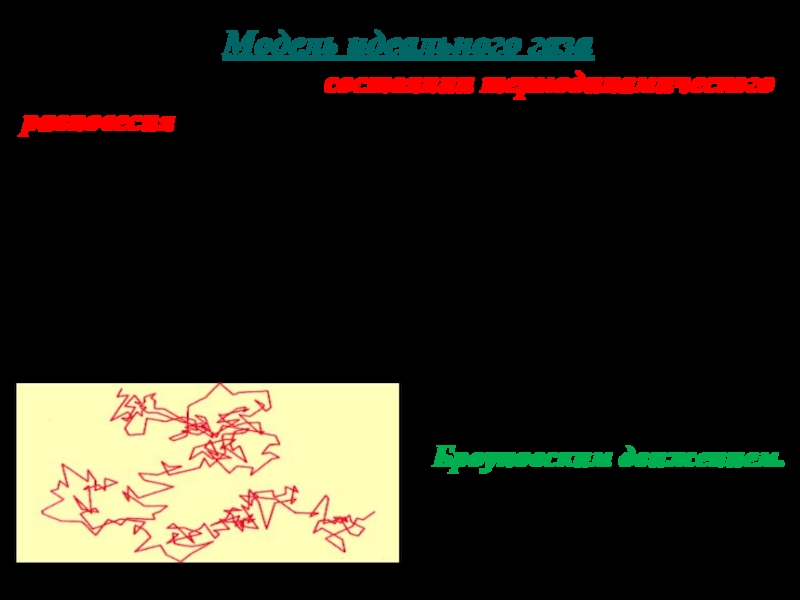
Если газ находится в состоянии термодинамического равновесия, атомы
и молекулы движутся хаотически (или беспорядочно). Это стало понято после
анализа экспериментальных данных, полученных английским ботаником Броуном. Он наблюдал с помощью микроскопа поведение спор растений, находящихся в воде. Споры двигались совершенно беспорядочно. Качественная картина движения показана на рисунке.
Такое движение было
названо
Броуновским движением.
Слайд 11Объясняется оно тем, что молекулы воды “толкают “ частицы спор
со всех сторон. Молекулы движутся беспорядочно и беспорядочные толчки заставляют
двигаться споры тоже беспорядочно.
Все направления движения молекул равновероятны.
Такое движение называется тепловым. Для достаточно разреженного газа в первом приближении можно пренебречь размерами молекул и их взаимодействием на малом расстоянии. Можно также считать, что столкновения молекул друг с другом и со стенками сосуда происходят упруго.
Слайд 12Силы взаимодействия молекул
На малых расстояниях действует сила отталкивания, на средних
расстояниях действует сила притяжения, на больших расстояниях сила не действует.
Слайд 13 Такое представление о газе называют моделью идеального газа:
Молекулы газа
рассматриваются как материальные точки, не имеющие собственного объема;
Молекулы не взаимодействуют
между собой на расстоянии и движутся прямолинейно и равномерно между двумя последовательными столкновениями;
Столкновение молекул между собой и со стенками сосуда носит упругий характер.
Газ при комнатной температуре и атмосферном давление можно рассматривать как идеальный.
Слайд 14Давление.
Давление газа на стенку сосуда – это результат столкновений
молекул с этой стенкой.
Итак, находящиеся под давлением газ или жидкость
действуют с некоторой силой на любую поверхность, ограничивающую их объем. В этом случае сила действует по нормали к ограничивающей объем поверхности. Давление на поверхность равно:
где ΔF – сила, действующая на поверхность площадью ΔS.
Слайд 15Основное уравнение молекулярно кинетической теории
Пусть имеется N частиц массой m0
в некотором кубическом сосуде. Так как молекулы движутся хаотически, то
движения в одном из шести независимых направлений пространства, совпадающих с осями декартовой системы координат, равновероятны. Примем допущение, что в каждом из этих направлении движется 1/6 N частиц. Пусть, кроме того, все частицы обладают одинаковой скоростью v.
Каждая из частиц, сталкивающихся со стенкой, передаёт ей импульс ΔP=2m0v.
Если площадь стенки S, а концентрация - n, то количество частиц, сталкивающихся со стенкой за время Δt равно N=(1/6)nSΔtv.
P=m0v
Слайд 16Так как давление
p=F/S,
а сила - это
импульс, передаваемый в единицу времени всеми частицами
F=(ΔP/Δt)N
то, подставив сюда соответствующие значения N и ΔP, получим
p=(1/3)m0nv2.
Если учесть, что Ek=mv2/2,
то
p=(2/3)nEk
Это основное уравнение молекулярно-кинетической теории газов: давление пропорционально концентрации газа и средней кинетической энергии движения молекул
Слайд 17Мы видим,что давление газов определяется средней кинетической энергией поступательного движения
молекул, находящихся в единице объема.
Единицы измерения давления.
По определению,
поэтому
размерность давления
1 Н/м2 = 1Па;
1 ат.(техн.)= 9,8 Н/см2 = 98066 Па
1 атм. (физ.)=101325 Па
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па
1 бар = 105 Па; 1 ат. = 0,98 бар.
Слайд 18Температура и средняя кинетическая энергия теплового движения молекул
Из опыта известно, что если привести в соприкосно-вение два тела:
горячее и холодное, то через некоторое время их температуры выровняются.
Понятие температуры вводится через понятия термодинамического равновесия и замкнутой (или изолированной) системы.
Замкнутой или изолированной системой называется система, тела которой не обмениваются энергией с окружающей средой.
Есть ли такие системы в окружающей нас действительности? Есть некое приближение к этой идеализации – система в адиабатической оболочке: сосуде Дьюара, термосе.
Слайд 19Опыт показывает: каково бы ни было состояние тел изолированной системы,
в ней в конце концов установится термодинамическое равновесие и прекратятся
все макроскопические процессы – это
ОБЩЕЕ (или НУЛЕВОЕ) НАЧАЛО термодинамики.
В состоянии т/д равновесия, как показывает опыт, тела обладают одинаковой степенью нагретости (температурой).
Если нагревать газ в сосуде единичного объема, то давление газа растет, увеличивается и температура
Поскольку концентрация молекул остается постоянной, из формулы
можно заключить, что при этом растет величина
Слайд 20Введем новое понятие – энергетическая температура :
,
Итак, энергетическая температура
– это средняя кинетическая энергия хаотического движения одной молекулы ( с точностью до коэффициента 2/3).
Слайд 21Измерять температуру научились задолго до того, как поняли физический смысл
температуры. Чтобы связать энергию с измеряемой температурой Т, Больцман ввел
коэффициент пропорциональности k, который впоследствии был назван его именем:
или
где k – постоянная Больцмана k = 1,38·10-23Дж·К-1.
Итак, мы ввели понятие температуры Т как величины, пропорциональной энергетической температуре, то есть средней кинетической энергии хаотического движения молекул.
Слайд 22Величину T называют абсолютной температурой и измеряют в Кельвинах (К).
Она служит мерой кинетической энергии теплового движения частиц идеального газа.
Можно видеть, что (3/2)k представляет собой среднюю кинетическую энергию теплового движения одной молекулы, приходящуюся на 1 кельвин.
Основное уравнение молекулярно-кинетической теории можно записать по другому.
Так как и
Отсюда
В таком виде основное уравнение молекулярно-кинетической теории употребляется чаще.
Слайд 23Так как температура определяется средней энергией движения молекул, то она,
как и давление, является статистической величиной, то есть параметром, проявляющимся
в результате совокупного действия огромного числа молекул. Поэтому не говорят: «температура одной молекулы», точнее сказать: «энергия одной молекулы, но температура газа».
Слайд 24Термометры. Единицы измерения температуры
Наиболее естественно было бы использовать
для измерения температуры определение
т.е. измерять кинетическую энергию поступатель-ного движения молекул газа. Однако практически невозможно проследить за молекулой газа.
Проще использовать зависимость P (T) или V(T). Такая зависимость используется в газовых термометрах. Газ является термометрическим ве-ществом, а P или V – термометрическим параметром.
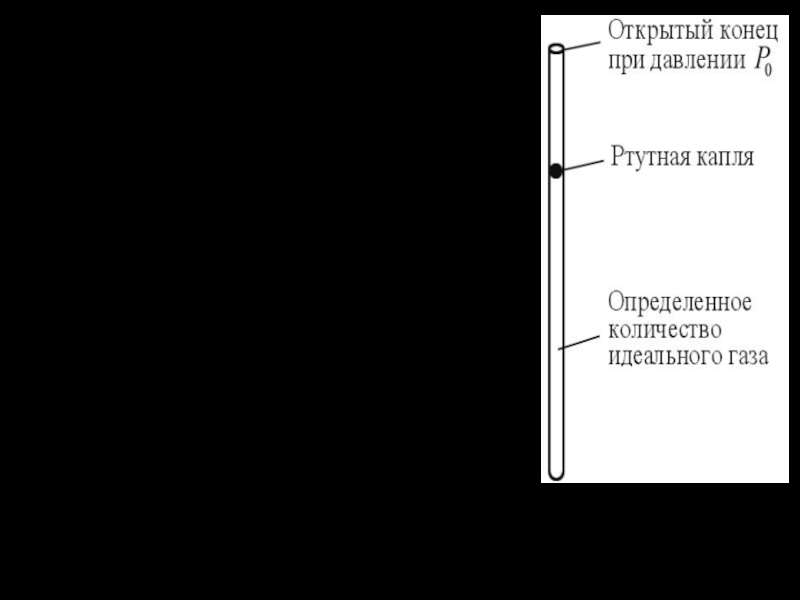
Слайд 25В качестве примера рассмотрим изображенный на рисунке простейший газовый термометр
с постоянным давлением. Пусть количество молекул в трубке — N,
объем газа в трубке — V. Тогда концентрация молекул n=N/V.
Из основного ур-я МКТ
получим
Видим, что объем V пропорционален температуре, а поскольку высота подъема ртутной капли пропорциональна V, то она пропорциональна и Т.
Слайд 26Если же в трубку вместо идеального газа поместить фиксированное количество
жидкой ртути, то мы получим обычный ртутный термометр. Хотя ртуть
далеко не идеальный газ, вблизи комнатной температуры ее объем изменяется почти пропорционально температуре.
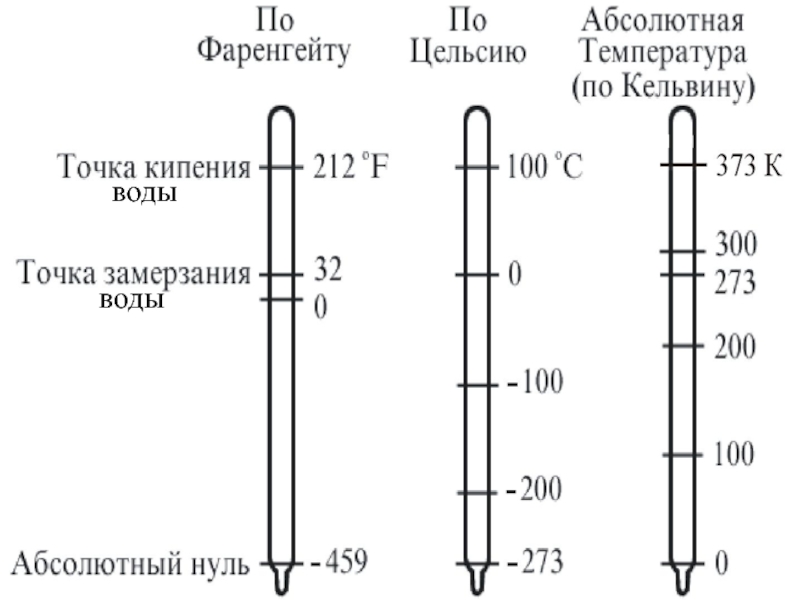
Слайд 27В физике и технике за абсолютную шкалу температур принята шкала
Кельвина, названная в честь знаменитого английского физика, лорда Кельвина.
1
К – одна из основных единиц системы СИ
Кроме того, используются и другие шкалы:
– шкала Фаренгейта (немецкий физик 1724 г.) – точка таянья льда 32F, точка кипения воды 212F.
– шкала Цельсия (шведский физик 1842г.) – точка таянья льда 0С, точка кипения воды 100С.
0С = 273,15 К.
На рис. приведено сравнение разных темп. шкал.
воды
воды
Слайд 28 Цельсий Андерс (1701 – 1744)
– шведский
астроном и физик.
Работы относятся к астрономии,
геофизике, физике. Предложил в 1742 г. стоградусную шкалу термометра, в которой за ноль градусов принял температуру таяния льда, а за 100 градусов – температуру кипения воды.
всегда, то и Т не может
быть
отрицательной величиной. При T = 0 (абсолютный ноль) P=0 .Шкалу Кельвина называют абсолютной шкалой температур
Связь между температурой Т, измеренной по шкале Кельвина, и температурой t, измеренной по шкале Цельсия:
Температура t по шкале Цельсия измеряется в градусах.
Слайд 30Уравнение состояния идеального газа
(уравнение Менделеева-Клапейрона)
Параметры состояния термодинамической системы закономерно связаны
между собой. Соотношение, определяющее связь между параметрами состояния системы, называется
уравнением состояния.
Получим такое уравнение для идеального газа.
Все газы, при нормальных условиях, близки по свойствам к идеальному газу. Ближе всех газов к идеальному газу – водород.
Слайд 31 Введем еще несколько понятий и величин.
Моль
- количество вещества, содержащее столько атомов (или молекул) сколько атомов
содержится в 0,012 кг изотопа углерода .
Моль любого вещества содержит одно и тоже число атомов (молекул) - число Авогадро:
Масса моля равна молекулярной массе, выраженной в граммах. Пример:
Число молей где m – масса газа,
N - число молекул
газа.
Слайд 32 Уравнение, связывающее основные параметры состояния идеального газа вывел
великий русский ученый Д.И. Менделеев.
Менделеев объединил известные ему
законы Бойля-Мариотта, Гей-Люссака и Шарля с законом Авогадро. Уравнение, связывающее все эти законы, называется уравнением Менделеева-Клапейрона и записывается так:
, здесь - число молей
Для одного моля можно записать:
где Vμ- объем одного моля (удельный объем)
Слайд 33 Получим это уравнение, используя основное уравнение молекулярно-кинетической теории:
Умножим
обе части уравнения на объем V:
здесь - общее число
молекул в объеме .
; ;
; введем
Окончательно получаем:
называется
универсальная газовая
постоянная. Она равна:
Закон Авогадро:
моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы.
При нормальных условиях этот объем равен
= 22,41·10-3 м3/моль.
Этот закон легко получить из уравнения Менделеева-Клайперона для . Нормальные условия:
Слайд 35Термодинамическим процессом называется переход системы из одного состояния в другое.
Такой переход всегда связан с нарушением равновесия системы. Например, при
сжатии газа давление в первую очередь возрастет вблизи поршня – равновесие нарушится.
Изопроцессы идеального газа
Слайд 36Нарушение равновесия будет тем значительнее, чем быстрее пере-мещать поршень. Если
двигать поршень очень медленно, то равно-весие нарушается незначительно и давление
в разных точках мало отличается от равновесного для данного объема газа. В пределе, при бесконечно медленном сжатии процесс окажется состоящим из последовательности равновесных состояний. Такой процесс называется равновесным или
квазистатическим.
Только такой процесс допустимо изображать графически.
Слайд 37Рассмотрим примеры квазистатических процессов.
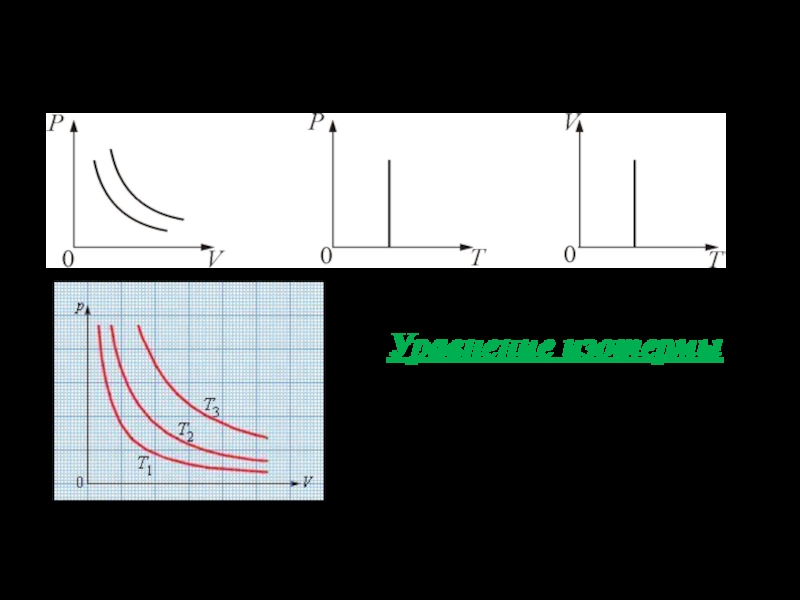
1. Изотермический процесс. T = const.
Изотермическим процессом
называется процесс, протекающий при постоянной температуре Т.
Поведение идеального
газа при изотермическом процессе подчиняется закону Бойля-Мариотта:
РV = const
«При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным».
График изотермического процесса на РV – диаграмме называется изотермой.
Слайд 38графики изотермического процесса на PV, VT и РT диаграммах:
Уравнение изотермы
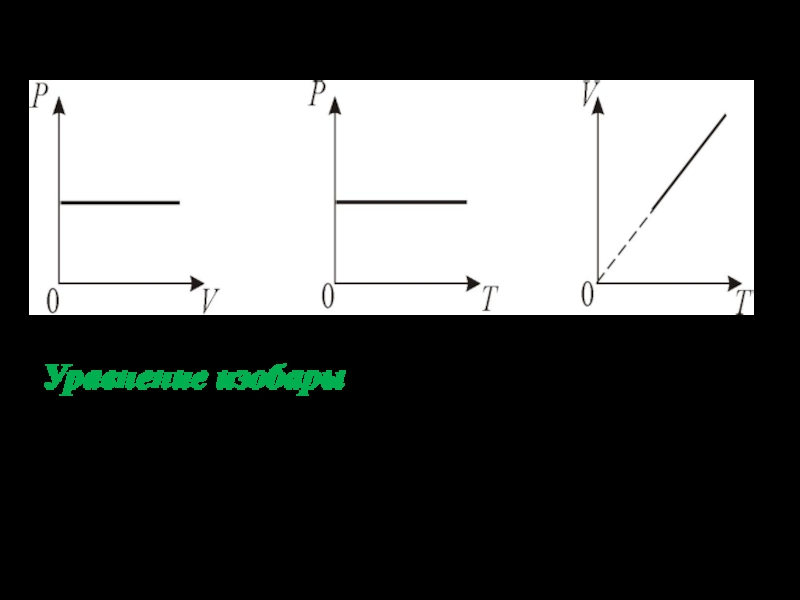
Слайд 392.Изобарический процесс. Р = const.
Изобарическим процессом называется процесс,
протекающий при постоянном давлении Р.
Поведение газа при изобарическом процессе
подчиняется закону Гей-Люссака:
V/T = const
«При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным».
График изобарического процесса на VT диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV и РT диаграммах.
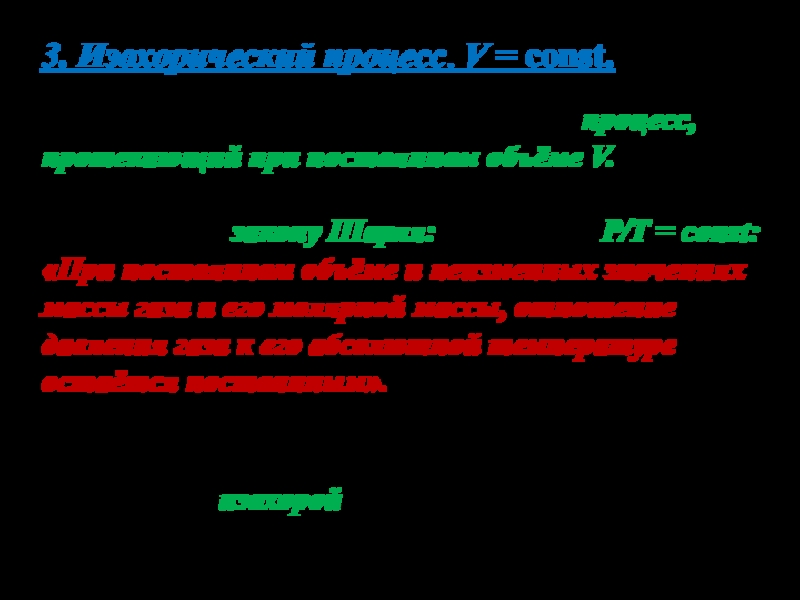
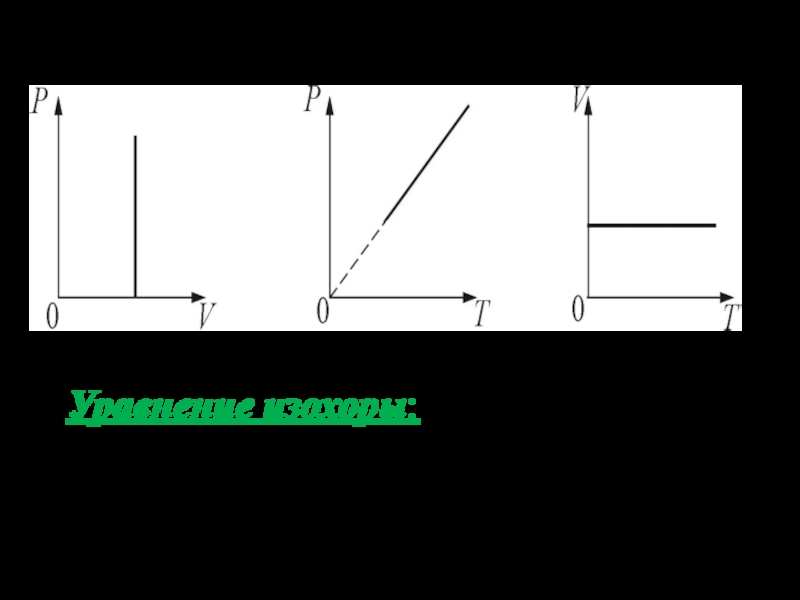
Слайд 413. Изохорический процесс. V = const.
Изохорическим процессом называется процесс, протекающий
при постоянном объёме V.
Поведение газа при этом изохорическом процессе
подчиняется закону Шарля: P/Т = const:
«При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным».
График изохорического процесса на РV диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ и VT диаграммах.
Слайд 434. Адиабатический процесс (изоэнтропийный).
Процесс, происходящий без теплообмена с окружающей
средой.
5. Политропический процесс.
Процесс, при котором теплоёмкость
газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.