Эллиптическая криптография со стандартом новым ЭЦП

называется гладкая кривая, задаваемая уравнением вида:
Y2 + a1XY +

Для глад­кости кривой не должно быть точек, в которых равны нулю обе частные производные, т.е два уравнения
a1Y = 3X2 + 2a2X+a4
2Y+a1X+a3 = 0
не должны одновременно удовлетворяться ни в одной точке.

Эллиптическая криптография

- положительное целое число, то
q называют характеристикой(characteristic) F и

Эллиптическая криптография

Char =2

суперсингулярные -

несингулярные

a1=0, также можно положить, a2 = 0

a3=0, также можно положить, a4 = 0

Не криптостойкие

Практически используют
ε4 : Y2+ХY= X3 +X2+1
ε5 : Y2+ХY= X3 +X2+ η , где η3 = η +1, η

общ­ности можно полагать, что a1=a3= 0 , а после упро­щения

Эллиптическая криптография

полем Fp y2=x3+ax+b , задаваемая коэффициентами a и b и

p- простое число – модуль эллиптической кривой, p>2255

и с введенной операцией сложения будем называть «группой». Для каждой

Число точек эллиптической кривой, включая точку О, называется порядком (order) кривой и обозначается E (Fp). (в ГОСТе m)

Пример 1. задана эллиптическая кривая E: Y2 = X3 + x+ 4 на поле F23. Точками кривой будут
(0,2) (0,21) (1, 11) (1,12) (4,7)
(4,16) (7,3) (7,20) (8,8) (8,15)
(9,11) (9,12) (10,5) (10,18) (11,9)
(11,14) (13,11) (13,12) (14,5) (14,18)
(15,6) (15,17) (17,9) (17,14) (18,9)
(18,14) (22,5) (22,19) O
Порядок группы #E(F23) = 29.

Порядок m группы точек эллиптической кривой может быть оценен с помощью неравенства:
p + 1 – 2√p ≤ m ≤ p + 1 + 2√p,
где р — порядок поля, над которым определена кривая

умножаться. Однако возможно скалярное умножение, когда соответствующее число раз выполняется

Порядком точки Р эллиптической кривой называется наименьшее положительное целое число r , такое что kP=0

Для кривой, определенной в примере 1, #E (F23) любая точка, кроме O, будет генератором E (F23) . Например, для точки P =(0,2) имеем:
1P = (0, 2) 2P = (13, 12) 3P = (11, 9)
4P = (1, 12) 5P = (7, 20) 6P = (9, 11)
7P = (15, 6) 8P = (14, 5) 9P = (4, 7)
10P = (22, 5) 11P = (10, 5) 12P = (17, 9)
13P = (8, 15) 14P = (18, 9 ) 15P = (18, 14)
16P = (8, 8) 17P = (17, 14) 18P = (10, 18)
19P = (22, 18) 20P = (4, 16) 21P = (14, 18)
22P = (15, 17) 23P = (9, 12) 24P = (7, 3)
25P = (1, 11) 26P = (11, 14) 27P = (13, 11)
28P = (0, 21) 29P = O.

Точка P будет называться генератором группы, если кратные ей точки образуют все множество точек эллиптической кривой.

две различные точки на кривой E. Тогда сумма P и

Сложение точек на эллиптической кривой

P + Q = R

P – точки R = (x3, y3) строится касательная к

ключом будем считать координаты точки P = xG на эллиптической кривой P, где G —

Координаты точки G вместе с коэффициентами уравнения, задающего кривую, являются параметрами схемы подписи и должны быть известны всем участникам обмена сообщениями. точка G должна иметь порядок q (2254 < q < 2256).

Приказом Федерального агентства по техническому регулированию и метрологии от 7

- содержит описание процессов формирования и проверки электронной цифровой подписи (ЭЦП), реализуемой с использованием операций в группе точек эллиптической кривой, определенной над конечным простым полем.

настоящего стандарта повышает, по сравнению с РАНЕЕ действовавшей схемой цифровой

Настоящий стандарт определяет

процессы формирования и проверки цифровой подписи под заданным сообщением (документом), передаваемым по незащищенным телекоммуникационным каналам общего пользования

эллиптической кривой;

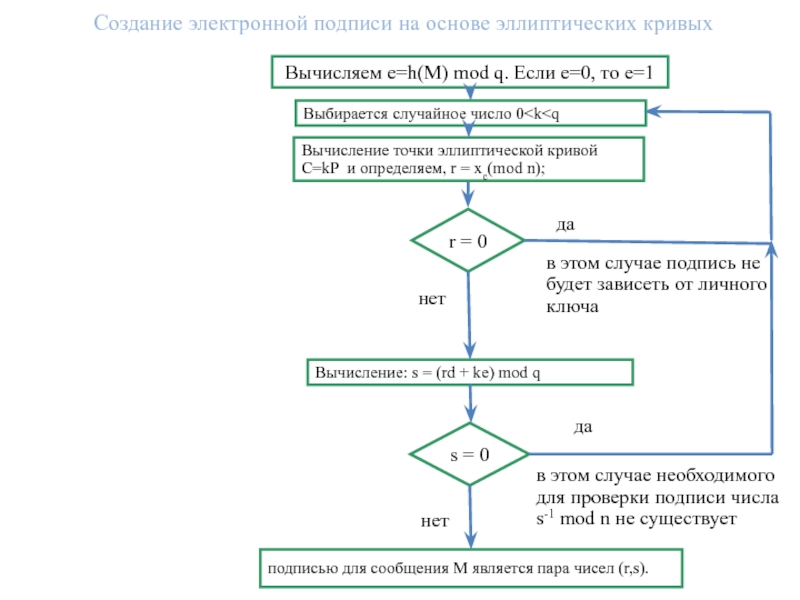
эллиптическая кривая Е , задаваемая коэффициентами а,b          ;

целое число m -

простое число q - порядок циклической подгруппы группы точек эллиптической кривой Е, для которого выполнены следующие условия:

точка Р≠О эллиптической кривой Е , с координатами             , удовлетворяющая равенству qP = О ;

хэш-функция  отображающая сообщения h (‘):V*→V представленные в виде двоичных векторов произвольной конечной длины, в двоичные вектора длины бит. Хэш-функция определена в ГОСТ Р 34.11-2012

(9)

обладать :

выполнить следующие действия (шаги) по

Шаг 1 - вычислить хэш-код сообщения

Шаг 2 - вычислить
Если е = 0, то определить е = 1.

Шаг 3 - сгенерировать случайное (псевдослучайное) целое число k ,
удовлетворяющее неравенству 0 < k < q .

Шаг 4 - вычислить точку эллиптической кривой C = kP и определить

Где -  -координата x точки С . Если r = 0, то вернуться к шагу 3

Шаг 5 - вычислить значение

Если s = 0, то вернуться к шагу 3.

Шаг 6 - определить цифровую подпись                                  как конкатенацию двух двоичных векторов.

кривая Ep(a,b). Число точек на ней должно делиться на большое

Выбирается точка Р на Ep(a,b)

Выбирается случайное число d [1, n-1]

Вычисляется Q = d × P

Личным ключом является d, открытым ключом - (E, P, n, Q).

число k [1, n-1]
Вычисление точки эллиптической кривой С=kP и

Проверяется, чтобы r не было равно нулю, так как в этом случае подпись не будет зависеть от личного ключа

r = 0

Выбирается другое
случайное число k

Вычисляется k-1mod n

Вычисляется: s = k-1 (Н(M) + dr) (mod n)

проверяется, чтобы s не было равно нулю, т.к. в этом случае необходимого для проверки подписи числа s-1 mod n не существует

s = 0

подписью для сообщения М является пара чисел (r,s).

да

нет

нет

да

Если e=0, то e=1
Выбирается случайное число 0

r = 0

Вычисление: s = (rd + ke) mod q

s = 0

подписью для сообщения М является пара чисел (r,s).

да

нет

нет

в этом случае подпись не будет зависеть от личного ключа

да

в этом случае необходимого для проверки подписи числа s-1 mod n не существует

сообщением М необходимо выполнить следующие действия (шаги) по алгоритму II:

Шаг

Шаг 3 - вычислить
Если е = 0, то определить е = 1.

Шаг 4 - вычислить значение

Шаг 5 - вычислить значения

Шаг 6 - вычислить точку эллиптической кривой  и определить

где  - x -координата точки С .

Шаг 7 - если выполнено равенство R = r , то подпись принимается.
В противном случае, подпись неверна.

проверки Q
Выходной результат-
свидетельство о достоверности или ошибочности данной

ϵ [0, n-1]
Подпись неверна
Вычислить w = s-1 (mod n) и

да

нет

Вычислить u1 = H(M) w (mod n)

Вычислить u2 = rw (mod n);

Вычислить v = x0 (mod n);

Вычислить u1P + u2Q = (x0, y0)

v = r

Подпись верна

да

нет

Проверка подписи

q
Подпись неверна
Вычислить e = h(M) mod q. Если e=0, то

да

нет

Вычислить v = e-1 mod q

z1 = sv (mod q), z2 = - rv (mod q);

Вычислить R = xc mod q;

Вычислить точку C эллиптической кривой z1P + z2Q

R= r

Подпись верна

да

нет

Проверка подписи

простое число р и параметры a и b для уравнения

В Ep(a,b) выбирается генерирующая точка G = (x1,y1). При выборе G важно, чтобы наименьшее значение n, при котором n × G = 0, оказалось очень большим простым числом

Параметры Ep(a,b) и G криптосистемы являются параметрами, известными всем участникам

P
P’
P’’
Х- общий секретный ключ для симметричного шифрования

ключ
Участник А вычисляет открытый ключ
PA = nA × G,

Участник В выбирает личный ключ nB и вычисляет открытый ключ PB = nB*G

Участники обмениваются открытыми ключами, после чего вычисляют общий секретный ключ K

Обмен ключами между пользователями А и В

участник А: K=nA * PB

участник B: K=nB * PA

общий секретный ключ представляет собой пару чисел. Если данный ключ предполагается использовать в качестве сеансового ключа для алгоритма симметричного шифрования, то из этой пары необходимо создать одно значение.

на эллиптической кривой Pm (x,y);
В качестве параметров рассматривается эллиптическая кривая

участник B выбирает личный ключ nB и вычисляет открытый ключ PB = nB × G

Чтобы зашифровать сообщение Pm используется открытый ключ получателя B PB

Участник А выбирает случайное целое положительное число k и вычисляет зашифрованное сообщение Cm, являющееся точкой на эллиптической кривой:
Cm = {k × G, Pm + k × PB}

Криптография с использованием эллиптических кривых. Шифрование.

вычитает результат из второй координаты:
Pm + k × PB

Участник А зашифровал сообщение Pm добавлением к нему kxPB. Противнику для восстановления сообщения придется вычислить k, зная G и k × G

Получатель также не знает k, но ему в качестве подсказки посылается k × G

Умножив k × G на свой личный ключ, получатель получит значение, которое было добавлено отправителем к незашифрованному сообщению

Тем самым получатель, не зная k, но имея свой личный ключ, может восстановить незашифрованное сообщение.

Криптография с использованием эллиптических кривых. Дешифрование.