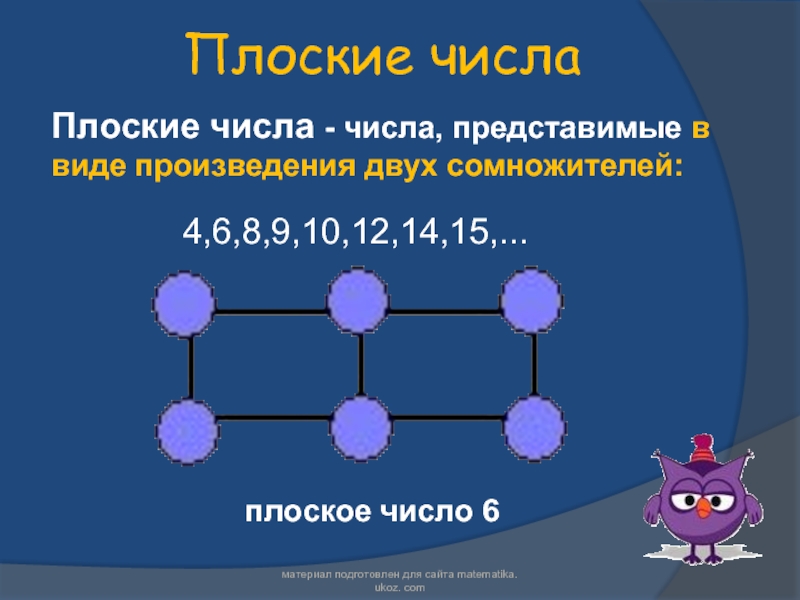
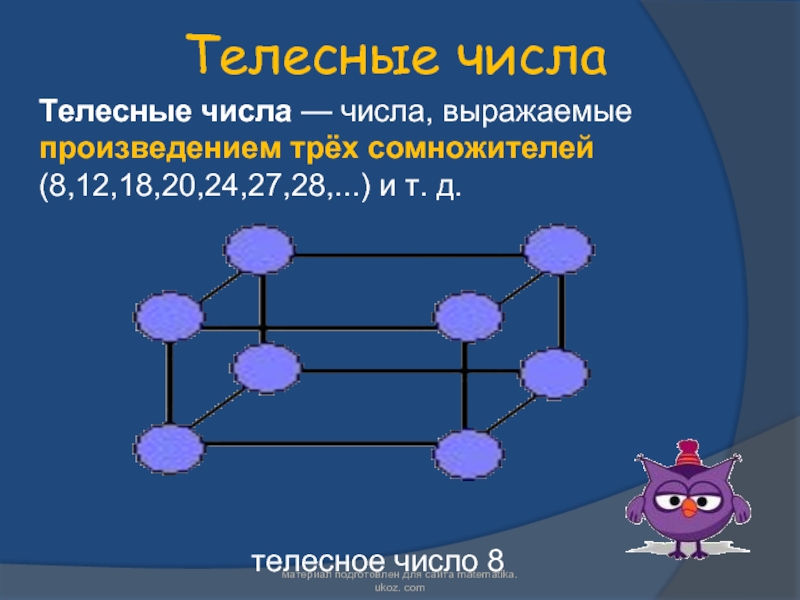
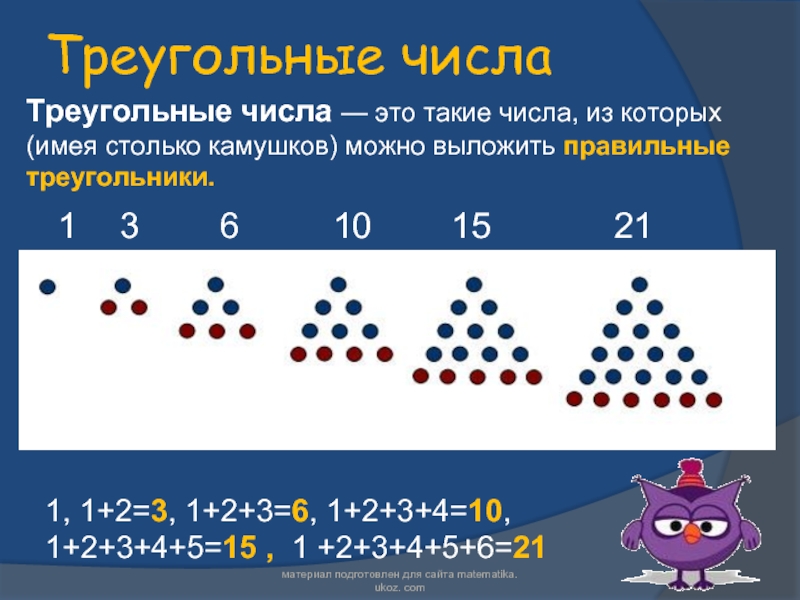
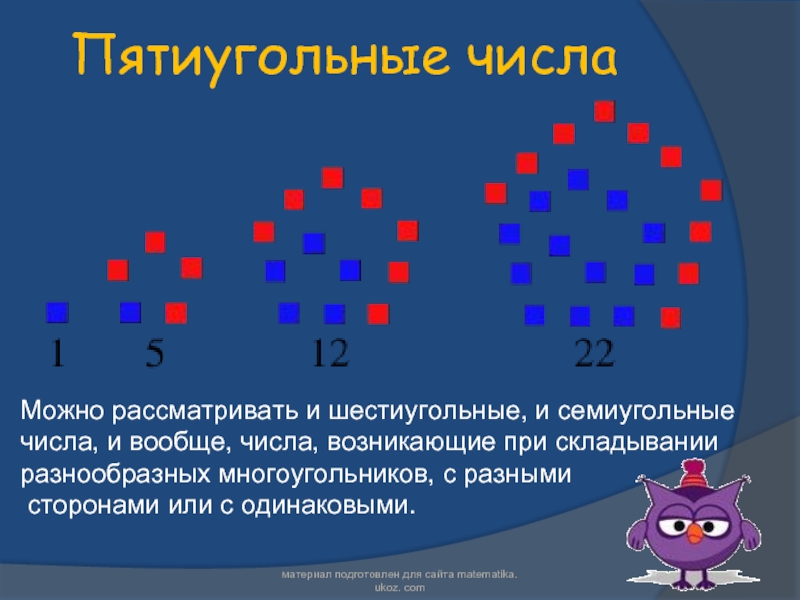
иной геометрической фигурой.
Предполагают, что впервые они появились в VI
веке до нашей эры – в школе Пифагора. В дальнейшем многие математики интересовались этими числамиматериал подготовлен для сайта matematika. ukoz. com