Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ФИНАНСОВАЯ МАТЕМАТИКА
Содержание
- 1. ФИНАНСОВАЯ МАТЕМАТИКА
- 2. Тема 2.ПОТОКИ ПЛАТЕЖЕЙ. проф.Угрозов Валерий Вячеславович
- 3. Потоки платежейФинансовые контракты могут предусматривать не
- 4. Наращенная сумма потока платежейНаращенная сумма потока платежей
- 5. Современная величина потока платежей Современная величина потока
- 6. Формула геометрической прогрессии Геометрическая прогрессияb, b*q, b*q2,
- 7. Основные параметры финансовой ренты Финансовой рентой
- 8. 1. Потоки платежей. Финансовая рента.
- 9. План накопительного фонда- по обычной годовой ренте
- 10. Формулы наращенной суммы S для финансовых
- 11. Пример 3.1. В течение 3-х лет на
- 12. Пример 3.3. В течение 3-х лет на
- 13. Рента р - срочная, с произвольным поступлением
- 14. Пример 3.5. В течение 3-х лет на
- 15. Современная (текущая) величина аннуитета-A Современная (текущая) величина
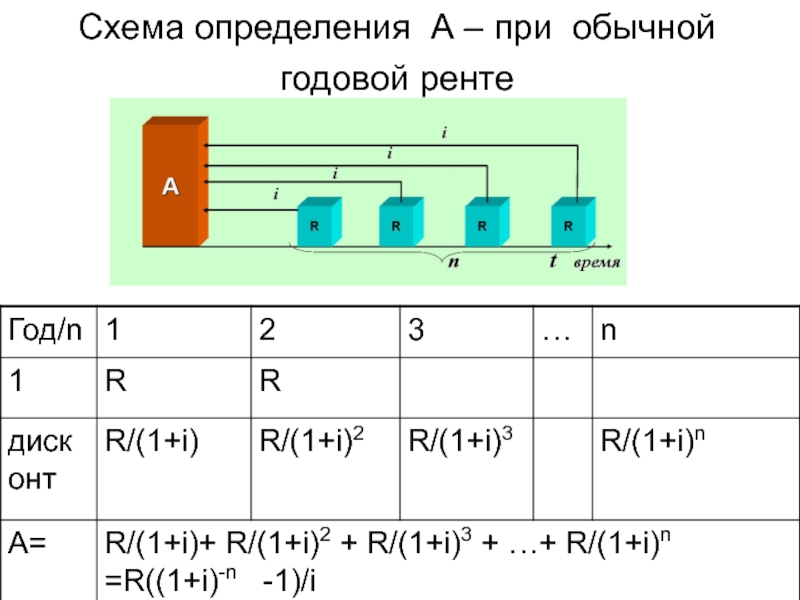
- 16. Cхема определения А – при обычной годовой ренте
- 17. Современная величина A обычной годовой финансовой ренты.
- 18. Пример 3.10. В течение 3-х лет на
- 19. Современная величина р-срочной финансовой ренты с произвольными
- 20. Пример 3.11. В течение 3-х лет на
- 21. Основные характеристики рент
- 22. Определение величины отдельного платежа простой ренты -
- 23. Пример 3.6. Через 3 года на расчетном
- 24. II-й случай. Определение величины отдельного платежа простой
- 25. Пример 3.7. Предприниматель взял кредит в размере
- 26. Определение срока простой ренты - nI-й
- 27. Пример 3.8. На момент окончания финансового соглашения
- 28. 2-й случай. Определение срока простой ренты n
- 29. Пример 3.9. Организация взяла кредит в размере
- 30. 1.3.5. Определение величины процентной ставки простой ренты
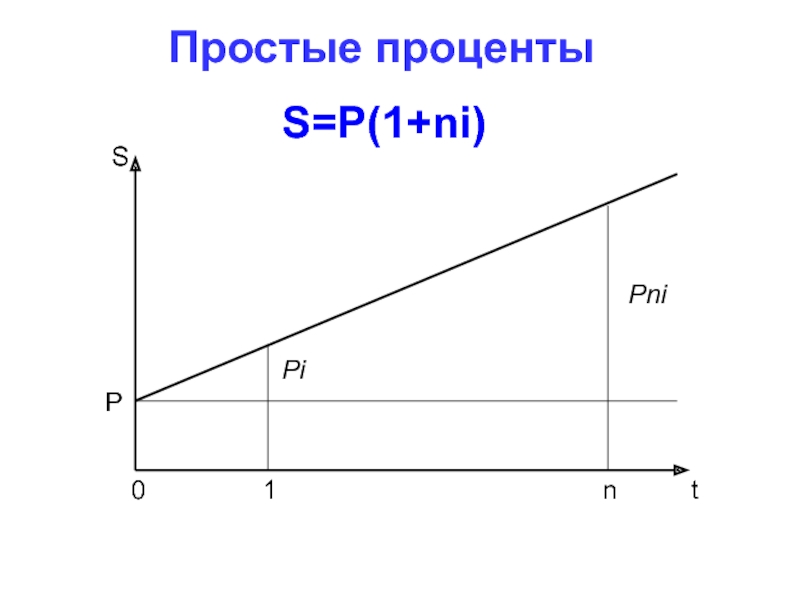
- 31. Простые процентыS=P(1+ni)
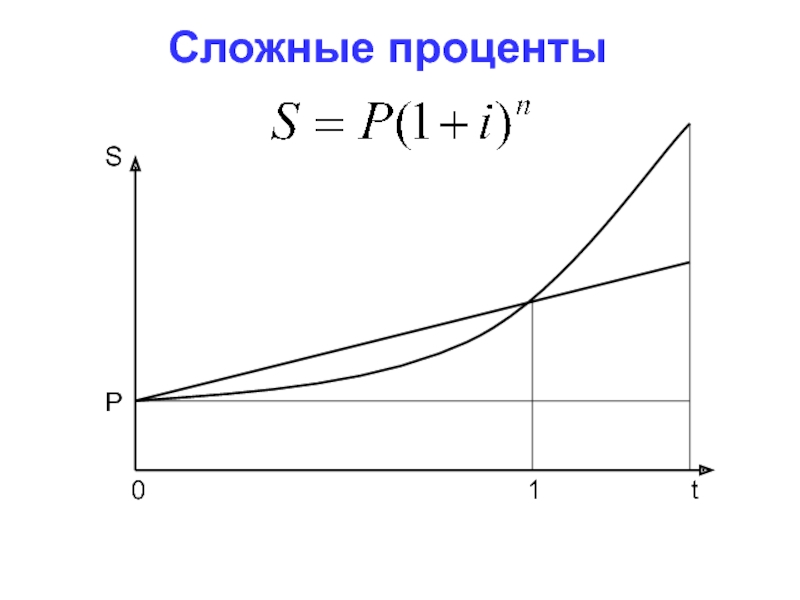
- 32. Сложные проценты
- 33. Учет налогов и начисление процентовВ ряде стран
- 34. СПАСИБО ЗА ВНИМАНИЕ !
- 35. Начисление процентов в условиях инфляцииСледствия инфляции: -
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3 Потоки платежей
Финансовые контракты могут предусматривать не отдельные разовые платежи,
а серию платежей, распределенных во времени (регулярные выплаты). Например, погашение
долгосрочного кредита, вместе с начисленными на него процентами; периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения (инвестиционный, пенсионный, страховой, резервный, накопительный и т.д.); дивиденды, выплачиваемые по ценным бумагам; выплаты пенсий из пенсионного фонда и пр.Поток платежей представляет собой ряд последовательных выплат и поступлений, причем выплаты выражаются отрицательными величинами, а поступления - положительными.
Обобщающими характеристиками потока платежей являются наращенная сумма - S и современная величина- A
Слайд 4Наращенная сумма потока платежей
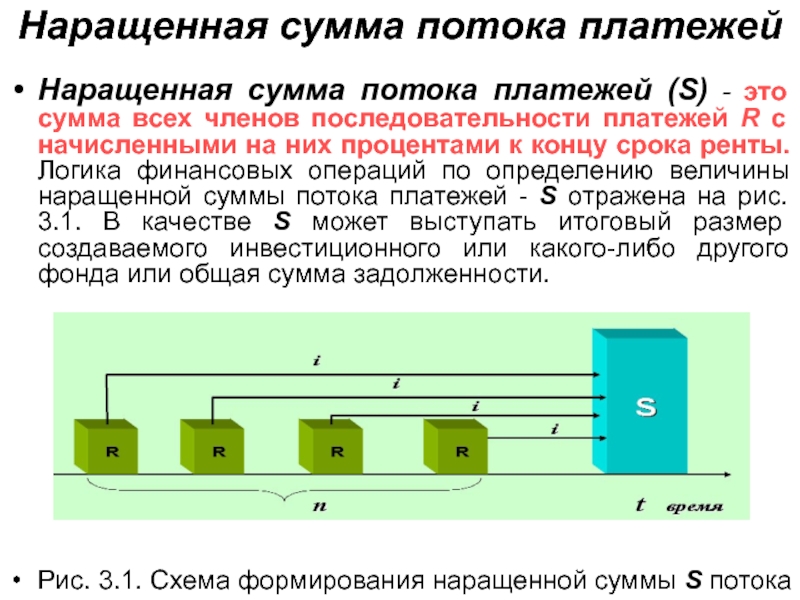
Наращенная сумма потока платежей (S) - это
сумма всех членов последовательности платежей R с начисленными на них
процентами к концу срока ренты. Логика финансовых операций по определению величины наращенной суммы потока платежей - S отражена на рис. 3.1. В качестве S может выступать итоговый размер создаваемого инвестиционного или какого-либо другого фонда или общая сумма задолженности.
Рис. 3.1. Схема формирования наращенной суммы S потока платежей
Слайд 5Современная величина потока платежей
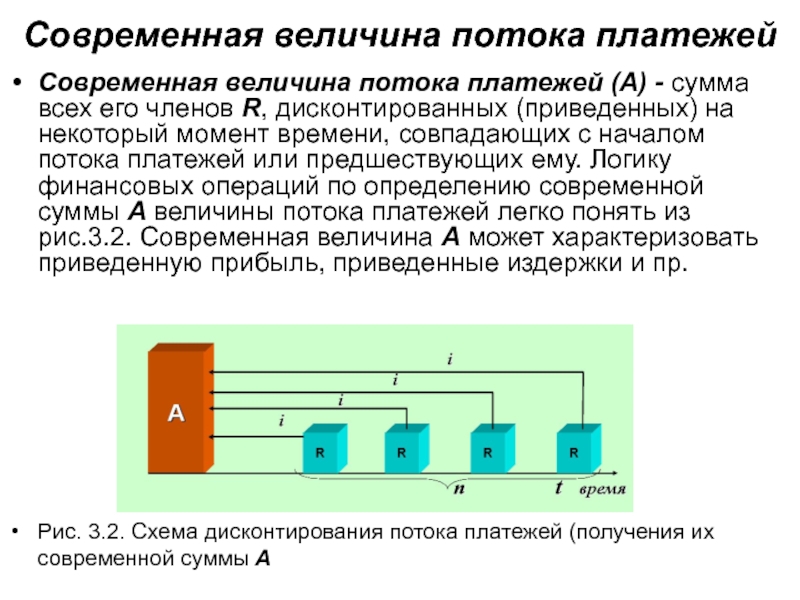
Современная величина потока платежей (А) -
сумма всех его членов R, дисконтированных (приведенных) на некоторый момент
времени, совпадающих с началом потока платежей или предшествующих ему. Логику финансовых операций по определению современной суммы A величины потока платежей легко понять из рис.3.2. Современная величина A может характеризовать приведенную прибыль, приведенные издержки и пр.
Рис. 3.2. Схема дисконтирования потока платежей (получения их современной суммы A
Слайд 6Формула геометрической прогрессии
Геометрическая прогрессия
b, b*q, b*q2, b*q3, b*q4,…, b*qn
Сумма геометрической прогрессии
S=b+b*q+b*q2+b*q3+b*q4+…+ b*qn
S=b*(qn-1)/(q-1)
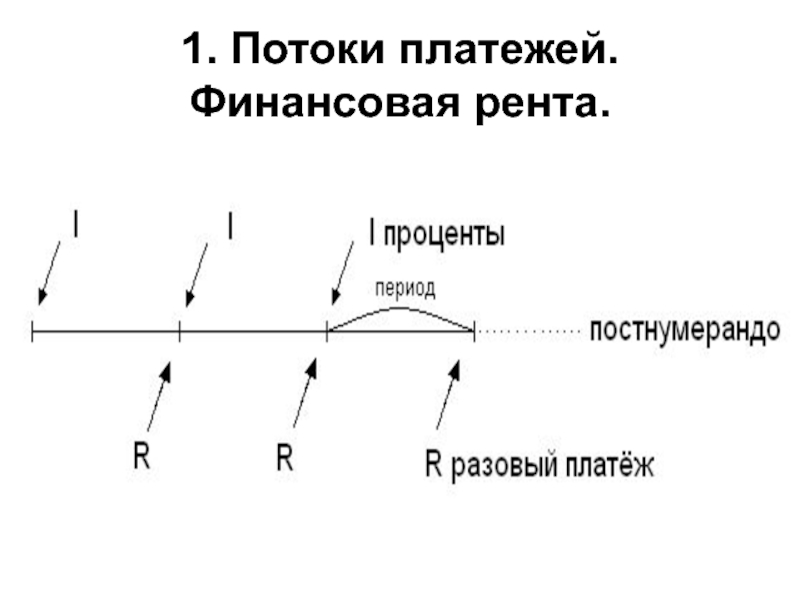
Слайд 7 Основные параметры финансовой ренты
Финансовой рентой (или аннуитетом) называют
поток платежей, все члены которого положительные величины, а временные интервалы
между ними постоянны.Финансовая рента имеет следующие параметры:
- член ренты (R) – величина каждого отдельного платежа выплачиваемая в 1 год (годовая выплата)
- период ренты – временной интервал между двумя соседними платежами,
- срок ренты (n) – время, измеренное от начала финансовой ренты до конца ее последнего периода,
- процентная ставка (i) – ставка, используемая при наращении или дисконтировании платежей, образующих ренту.
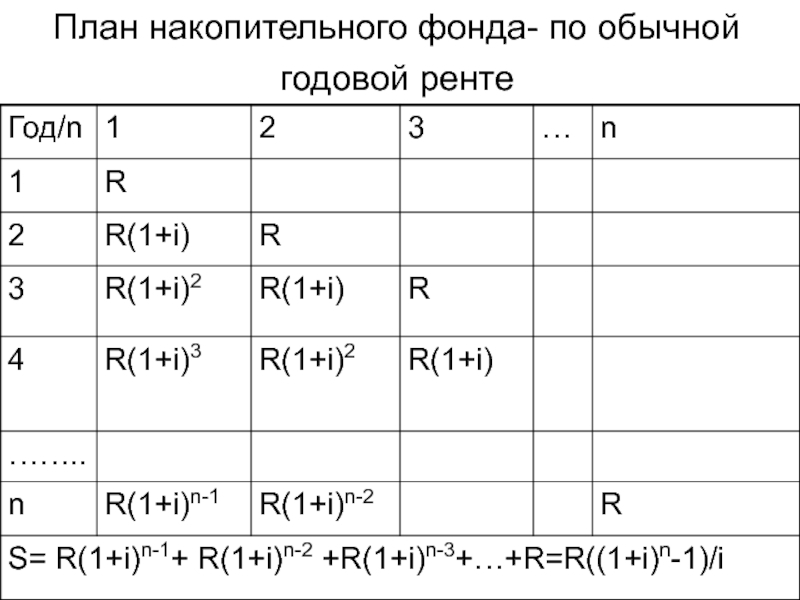
Слайд 10 Формулы наращенной суммы S для финансовых рент
Обычная годовая рента.
Пусть в конце каждого года в течение n лет на
расчетный счет вносится по R рублей, сложные проценты начисляются один раз в год по ставке i. В этом случае первый взнос к концу срока ренты возрастет до величины R(1+i ) n-1, так как на сумму R проценты начислялись в течение (n -1) года. Второй взнос увеличится до R(1+i)n-2 и т.д. На последний взнос – R проценты не начисляются. Таким образом, в конце срока ренты ее наращенная сумма будет равна сумме членов геометричес-кой прогрессии:S=R+R(1+i)+R(1+i)2+…+R(1+i)n-1 ,в которой первый член равен R, знаменатель (1+i), число членов n. Отсюда:S = R*sn;i , (3.1)
где s n;i = [(1+i)n -1]/i - коэффициент наращения ренты. S зависит от срока ренты n и уровня процентной ставки i.
Слайд 11Пример 3.1. В течение 3-х лет на расчетный счет в
конце каждого года поступает по 10 млн руб., на которые
1 раз в год начисляются проценты по сложной годовой ставке в 10%. Определить сумму на расчетном счете к концу указанного срока.Дано:n = 3 года,R = 10 000 000 руб.,m =1, p=1, i = 0,10 .Найти S = ?
Решение Вычисления производится по формуле для обычной годовой ренты по формуле (3.1) S = 10 000 000*[(1+ 0,1)3 - 1] / 0,1 = 33 100 000,00 руб.
Слайд 12Пример 3.3. В течение 3-х лет на расчетный счет в
конце каждого квартала поступают платежи равными долями из расчета 10
млн руб. в год (т.е. по 10/4 млн. руб. в квартал), на которые в конце каждого года начисляются проценты по сложной ставке в 10% годовых. Определить сумму на расчетном счете к концу указанного срока.Дано:n = 3 года,m = 1,R = 10 000 000 руб., p = 4,i = 0,10.
Найти S = ?
Решение Вычисления проведем по формуле (3.3):
S = (10 000 000/4)*[(1+0,1)3 - 1]/ [(1+0,1) 1/4 - 1] =34 316 60,35 руб.
Слайд 13Рента р - срочная, с произвольным поступлением платежей p ≥
1, и произвольным начислением процентов m ≥ 1 (общий случай).
Наращенная
сумма рассчитывается по формуле: S =s1+s2+…+snp = (3.5)
Слайд 14Пример 3.5. В течение 3-х лет на расчетный счет в
конце каждого квартала поступают платежи (р=4) равными долями из расчета
10 млн руб. в год (т.е. по 10/4 млн руб. в квартал), на которые ежемесячно (m=12) начисляются проценты по сложной ставке в 10% годовых. Определить сумму на расчетном счете к концу указанного срока.Дано:n = 3 года, m = 12,R = 10 000 000 руб.,
p = 4, j = 0,10 .Найти S = ?
Решение.
Вычисляя по формуле (3.5) находим:
S = (10 000 000/4)*[(1+0,10/12) (12х3) -1] / [(1+0,10/12) (12/4) -1] =34 529 637,96 руб.
Слайд 15Современная (текущая) величина аннуитета-A
Современная (текущая) величина потока платежей (капитализированная
или приведенная величина) – это сумма платежей, дисконтированных на момент
начала ренты по ставке начисляемых сложных процентов. Это важнейшая характеристика финансового анализа, т.к. является основой для измерения эффективности различных финансово-кредитных операций, сравнения условий контрактов и т.п.Данная характеристика показывает, какую сумму-A следовало бы иметь первоначально, чтобы, разбив ее на равные взносы - R, на которые начислялись бы установленные проценты в течение всего срока –i , можно было бы получить указанную наращенную сумму - S.
Слайд 17Современная величина A обычной годовой финансовой ренты.
Если член годовой
ренты равен R, процентная ставка i, срок ренты n и
проценты начисляются один раз в конце года. Тогда a1,a2,…an- приведенные к началу ренты величины первого, второго и т.д. платежей :где - дисконтный множитель.
Приведенные величины-a1,a2,…,an- образуют геометрическую прогрессию, сумма которой равнаA:
(3.14)
где - коэффициент приведения ренты.
Слайд 18Пример 3.10. В течение 3-х лет на расчетный счет в
конце каждого года (p = 1) поступает по 10 млн
руб. Ежегодное дисконтирование производится по сложной процентной ставке в 10% годовых. Определить современную стоимость ренты.Дано:n = 3 года, m = 1,R = 10 000 000 руб,
p = 1, j = 0,10. Найти A = ?
Решение.
Вычисляя по формуле (3.14) получим :
А = 10 000 000*[1 - (1+0,1) -3]/0,1 = 24 868 519,91 руб.
Слайд 19Современная величина р-срочной финансовой ренты с произвольными значениями p ≥
1 и m ≥ 1.
Формула (3.15) является общей для
нахождения современной величины ренты, когда р и т могут принимать произвольные значения (3.15)Слайд 20Пример 3.11. В течение 3-х лет на расчетный счет в
конце каждого квартала поступают платежи (р=4) равными долями из расчета
10 млн. руб. в год (т.е. по 10/4 млн руб. в квартал). Ежемесячное дисконтирование (m=12) производится по сложной ставке 10% годовых. Определить современную стоимость ренты.Дано:n = 3 года,m = 12, R = 10 000 000 руб.,
p = 4, j = 0,10. Найти A = ?
Решение
Вычисляя по формуле (3.15) получим:
А = (10 000 000/4)*[1 - (1+0,1/12) (-3*12)] /[(1+0,1/12)](12/4) -1] = 25 612 003,42 руб.
Слайд 22Определение величины отдельного платежа простой ренты - R.
I. Известна величина
наращенной суммы-S , а также процентная ставка i и срок
ренты n.Величина отдельного платежа- R по схеме постнумерандо. (3.6)
Величина отдельного платежа по схеме пренумерандо (3.7)
Слайд 23Пример 3.6. Через 3 года на расчетном счете необходимо иметь
10 млн руб. Определить размер ежегодных платежей : а) в
конце года (постнумерандо);в) в начале года - пренумерандо по сложной процентной ставке 12% годовых.Дано: n = 3 года,S = 10 000 000 руб.,i = 0,12 .
Найти Rпо и Rпр= ?
Решение.
а) Вычисляя по формуле (3.6)находим: Rпо= 10 000 000*0,12/[(1+0,12)3 -1] = 2 963 489,81 руб.
в) Вычисляя по формуле (3.7) находим: Rпр = (10 000 000*0,12)/[(1+0,12)((1+0,12)3 -1)] = 2 645 973,04 руб.
Слайд 24II-й случай. Определение величины отдельного платежа простой ренты при известной
современной стоимости A.
Известна современная стоимость- A, процентная ставка- i,количество выплат-
n.Величина отдельного платежа по схеме постнумерандо. (3.8)
Величина отдельного платежа по схеме пренумерандо (3.9)
Слайд 25Пример 3.7. Предприниматель взял кредит в размере 10 млн руб.
сроком на 3 года под 14% годовых. Рассчитать размер ежегодных
погасительных платежей, если они будут выплачиваться a) в конце года ; b)в начале годаДано: n = 3 года,A = 10 000 000 руб.,i = 0,14 .Найти Ra и Rb = ? Решение.
а) Вычисляя по формуле (3.8) находим:
Ra=
= 10 000 000*0,14/[1-1/(1+0,14)3] = 4 307 314,80 руб.
b) Вычисляя по формуле (3.9) находим:
R = (10 000 000*0,14)/[(1+0,14)(1-/(1+0,14)3)] = 3 778 346,32 руб.
Слайд 26 Определение срока простой ренты - n
I-й случай. Известна наращенная
сумма-S , процентная ставка-i , отдельный платеж -R
Срок простой
ренты при платежах по постнумерандо. (3.10)Срок простой ренты при платежах по пренумерандо. (3.11)
Слайд 27Пример 3.8. На момент окончания финансового соглашения заемщик должен выплатить
30 000 000 руб. Платежи размером 5 000 000 руб. поступают ежегодно в конце
года, с начислением по сложной процентной ставке 15% годовых. Определить срок простой ренты a)постнумерандо;в)пренумерандоДано:R = 5 000 000 руб.,S = 30 000 000 руб.,
i = 0,15 .Найти na и nb= ? Решение.
a) По формуле (3.10) находим:
na = ln (1+30 000 000*0,15/5 000 000) / ln(1+0,15) = 4,59 года.
в) По формуле (3.11) находим: nв = ln(1+30 000 000*0,15/(5 000 000*(1+0,15)) / ln(1+0,15) = 4,14 года.
Слайд 282-й случай. Определение срока простой ренты n при известной современной
стоимости ренты A
Известна современная стоимость- A, отдельный платеж ренты –
R, процентная ставка- i. Определение срока простой ренты при платежах по постнумерандо: (3.12)
Определение срока простой ренты при платежах по пренумерандо (3.13)
Слайд 29Пример 3.9. Организация взяла кредит в размере 30 000 000 руб. с
условием погашения ежегодными платежами по 6 000 000 руб. и начислением по
сложной процентной ставке 15% годовых. Определить срок простой ренты при погашении: a) в конце года (постнумерандо); b) в начале года (пренумерандо)Дано: A = 30 000 000 руб., R = 6 000 000 руб.,
i = 0,15. Найти na и nb = ?
Решение.
a)Вычисляя по формуле (3.12) находим: n = - ln (1-30 000 000*0,15/6 000 000) / ln(1+0,15) = 9,92 года.
a)Вычисляя по формуле (3.13) находим
n = -ln (1-30 000 000*0,15/(6000 000*(1+0,15)) / ln(1+0,15) = 7,56 года.
Слайд 301.3.5. Определение величины процентной ставки простой ренты
При заключении финансовых
сделок важно знать их доходность, которая определяется процентной ставкой ренты
за один период начисления. При этом считается, что известны следующие значения: отдельный платеж R, срок займа n и наращенная сумма S (или современная стоимость А). В Excel данная задача решается с помощью финансовой функции СТАВКА.Слайд 33Учет налогов и начисление процентов
В ряде стран проценты, получаемые кредитором,
облагаются налогом, что уменьшает реально получаемую наращенную сумму. Пусть S
– наращенная сумма до уплаты налога, С – после уплаты налога, g – ставка налога. Тогда получаем сумму налога Ig=(S-P)g, а наращенная сумма после уплаты налога составитC=S-Ig=P(1+n(1-g)i)
Вывод: учет налога сводится к сокращению процентной ставки – для получения реального наращения следует вместо ставки i применять ставку (1-g)i.
Слайд 35Начисление процентов в условиях инфляции
Следствия инфляции: - падение покупательского спроса
денег (индекс ),
- рост цен (индекс
роста цен =1/ ).Пример: в начале года за 1 руб. покупали 100 г сахара, в конце – 90 г.
Наращенная сумма С с учетом покупательской способности денег составит
,
где – скорректированный на инфляцию множитель наращения.