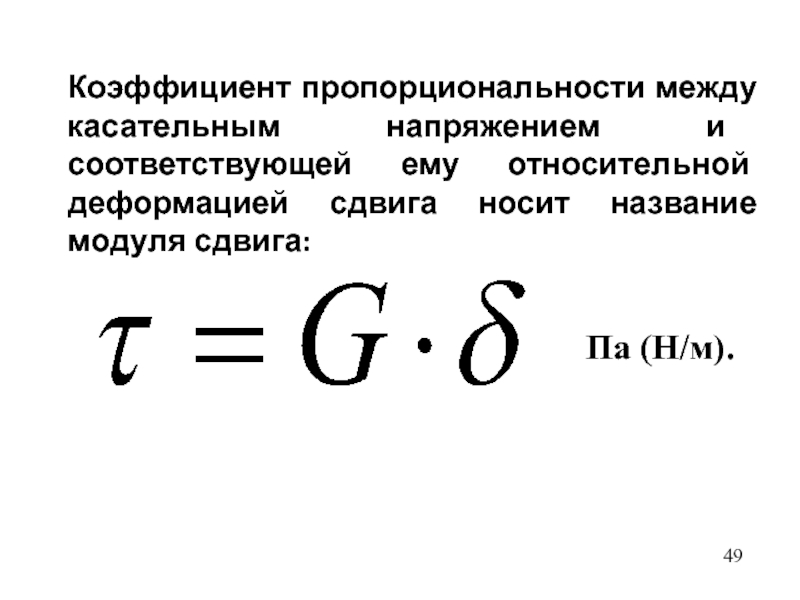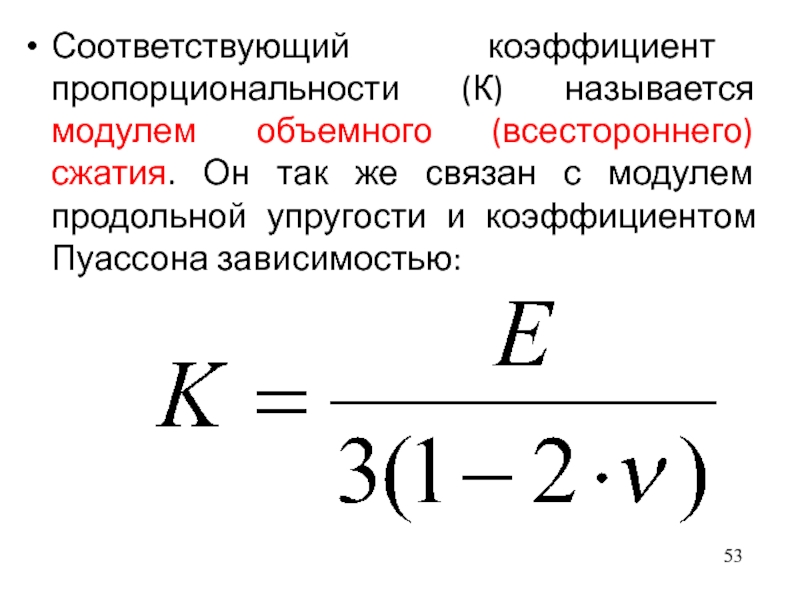Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика горных пород
Содержание
- 1. Физика горных пород
- 2. Удельный и объемный весУдельным весом называется вес
- 3. Механические свойстваК механическим свойствам горных пород относятся
- 4. Механические свойстваМеханические свойства горных пород характеризуются следующими
- 5. Упругие свойстваЧастые знакопеременные нагрузки на горную породу
- 6. Пластические свойстваКоэффициент пластичностиМодуль деформацииПараметры ползучестиПериод релаксацииДлительная прочностьПредел длительной прочностиРеологические свойства
- 7. Механические свойства горных пород характеризуются следующими параметрами.
- 8. Напряжения и деформацииНапряжение - величина векторная и
- 9. FNTAРассмотрим образец, на грань которого действует сила
- 10. F - сила действующая на образец горной
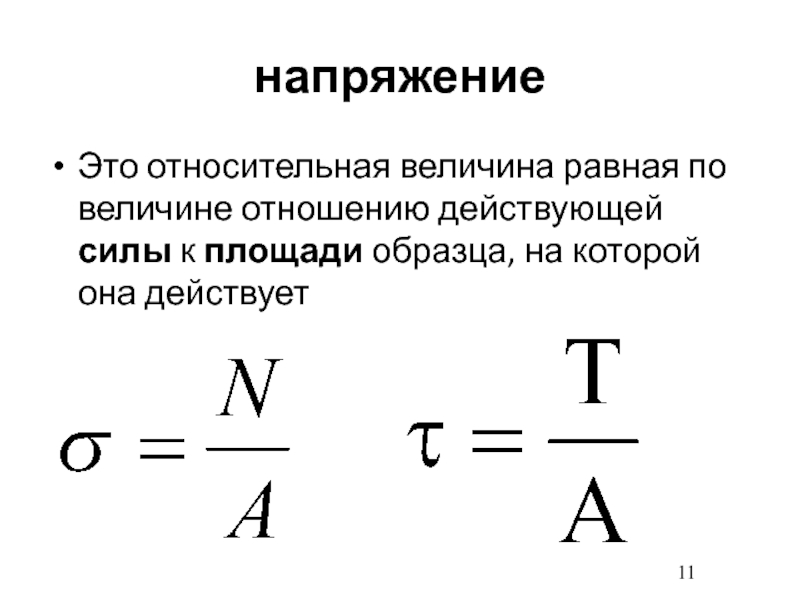
- 11. напряжение Это относительная величина равная по величине
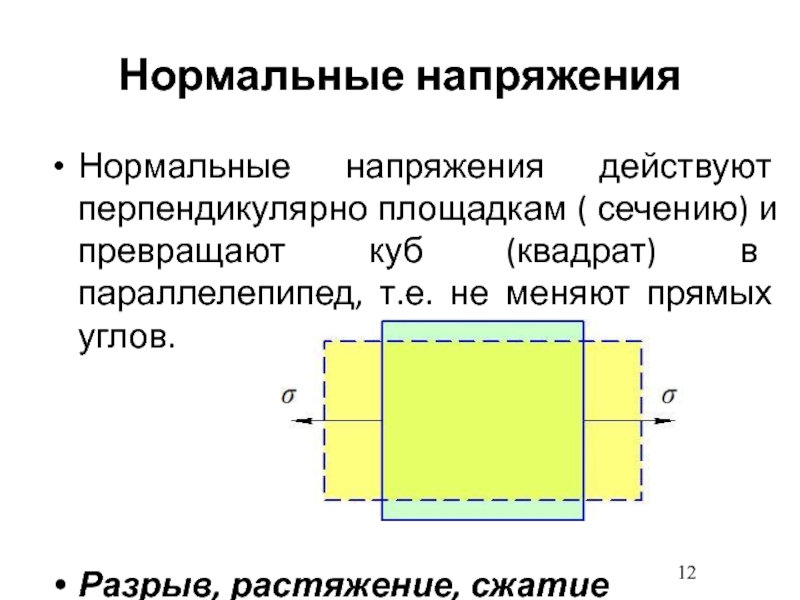
- 12. Нормальные напряженияНормальные напряжения действуют перпендикулярно площадкам (
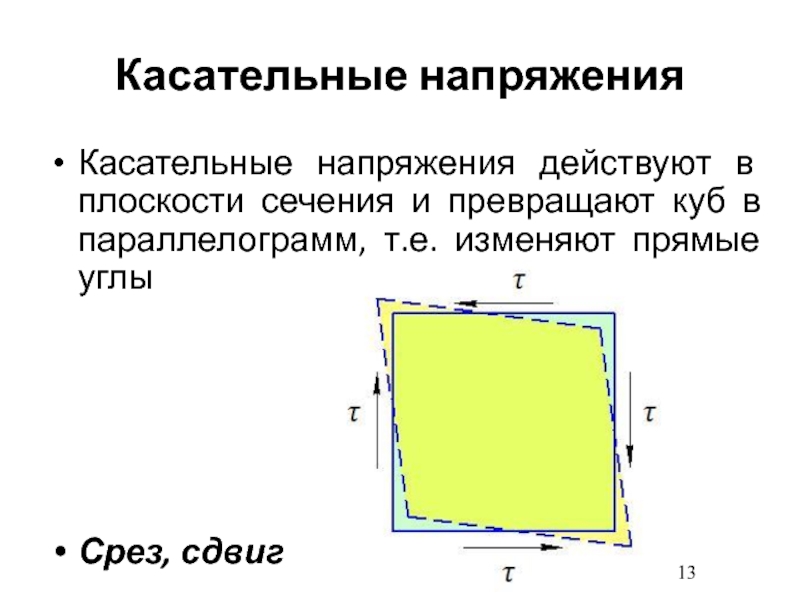
- 13. Касательные напряженияКасательные напряжения действуют в плоскости сечения
- 14. Напряжения в системе СИ выражаются в паскалях
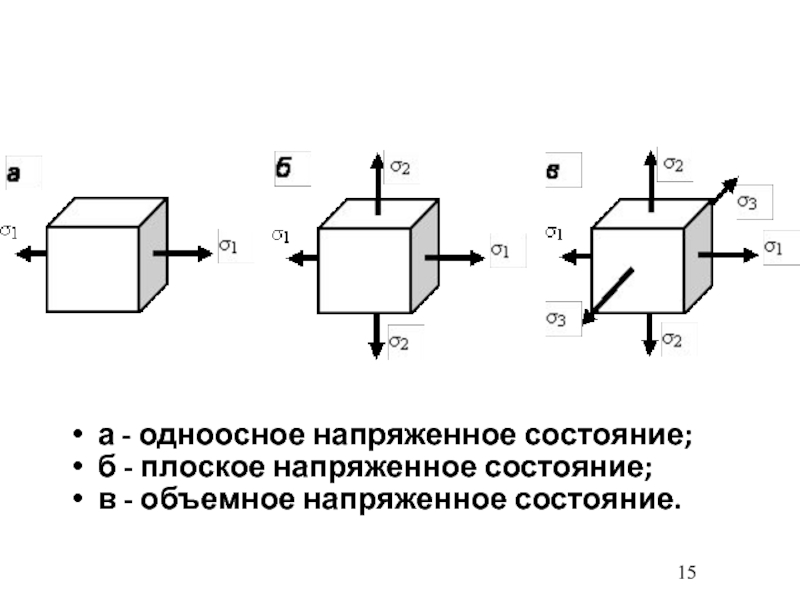
- 15. а - одноосное напряженное состояние;б - плоское напряженное состояние;в - объемное напряженное состояние.
- 16. Схема напряжений, отнесенная к произвольной системе координат
- 17. Тензор напряженийНапряжения, действующие на гранях бесконечно малого параллелепипеда, можно записать в виде таблицы, называемой тензором напряжений:
- 18. Нормальные напряжения снабжаются индексом, который указывает координатную
- 19. В любом поле напряжений можно найти такие
- 20. Тензор напряжений в главных осях имеет следующий вид:
- 21. Слайд 21
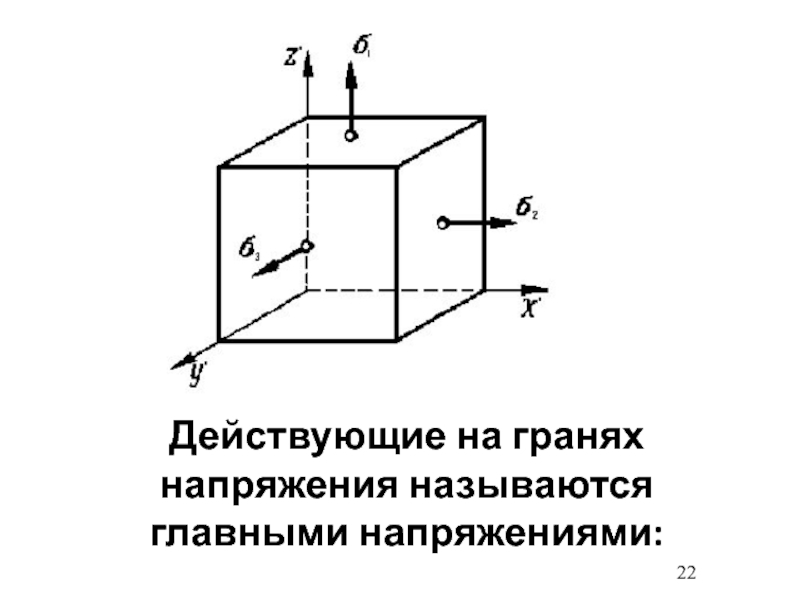
- 22. Действующие на гранях напряжения называются главными напряжениями:
- 23. Нормальные напряжения 1, 2, 3 являются главными
- 24. Плоское напряженное состояниеЕсли все векторы напряжений параллельны
- 25. Напряженное состояние на любой площадке образца породы
- 26. Слайд 26
- 27. Значения касательного и нормального напряжений в любой
- 28. В плоскости под углом к главным
- 29. Круги Мора
- 30. Практически же площадь, на которую воздействуют силы,
- 31. Слайд 31
- 32. Напряжения в породах могут возникать не только
- 33. Под действием внешних сил горная порода испытывает
- 34. Деформация образца породы под действием нормальных (σ) напряжений
- 35. Линейные деформацииПо направлению действующей силы деформации называются
- 36. Эти деформации измеряются непосредственно в лабораторных опытах
- 37. Микрометры
- 38. Тензорезисторы
- 39. Испытания образца породы на винтовом прессе
- 40. Слайд 40
- 41. Относительные линейные деформации
- 42. Деформация образца породы под действием касательных () напряженийδСдвиг граней образцапод действием касательныхнапряжений
- 43. Деформация сдвига δ определяется по величине tg
- 44. Деформации, по действию, могут быть разрушающие и
- 45. Слайд 45
- 46. В случае упругих деформаций наблюдается прямая зависимость
- 47. Области деформации пород
- 48. Коэффициент пропорциональности между действующим продольным напряжением (растягивающим
- 49. Коэффициент пропорциональности между касательным напряжением и соответствующей ему относительной деформацией сдвига носит название модуля сдвига:Па (Н/м).
- 50. На практике часто пользуются еще одним упругим
- 51. В случае идеально упругих тел достаточно знать
- 52. В условиях равномерного упругого трехосного сжатия породы
- 53. Соответствующий коэффициент пропорциональности (К) называется модулем объемного
- 54. Скачать презентанцию
Удельный и объемный весУдельным весом называется вес единицы объема абсолютно сухой породы без учета пор и трещин. УДЕЛЬНЫЙ ВЕС – отношение веса тела к занимаемому им объему. Он равен отношению массы твердой фазы
Слайды и текст этой презентации
Слайд 1Физика горных пород
Лекция 3 – механические свойства горных пород
Лектор: Шульгин
Павел Николаевич
Слайд 2Удельный и объемный вес
Удельным весом называется вес единицы объема абсолютно
сухой породы без учета пор и трещин.
УДЕЛЬНЫЙ ВЕС –
отношение веса тела к занимаемому им объему. Он равен отношению массы твердой фазы к ее объему.ОБЪЕМНЫЙ ВЕС - отношение веса руды или породы (твердой, жидкой и газообразной фаз) к ее объему – вес единицы объема сухой породы в естественном пористом состоянии.
Слайд 3Механические свойства
К механическим свойствам горных пород относятся все свойства, которые
проявляются при статическом и динамическом воздействии твердых тел на породу.
В зависимости от величины и длительности воздействия могут проявиться:прочностные;
упругие;
реологические свойства горных пород.
Слайд 4Механические свойства
Механические свойства горных пород характеризуются следующими параметрами.
Предел прочности горных
пород на сжатие σсж
Он характеризуется максимальным значением напряжения, выдерживаемого породой.
Другие показатели прочности намного ниже этой величины, а минимальное значение имеет предел прочности на растяжение σр.
Слайд 5Упругие свойства
Частые знакопеременные нагрузки на горную породу вызывают появление в
ней упругих колебаний. К основным упругим характеристикам породы относятся:
• модуль
упругости - Е, Па;• коэффициент Пуассона - ν;
• модуль сдвига G, Па.
Слайд 6Пластические свойства
Коэффициент пластичности
Модуль деформации
Параметры ползучести
Период релаксации
Длительная прочность
Предел длительной прочности
Реологические свойства
Слайд 7Механические свойства горных пород характеризуются следующими параметрами.
Предел прочности горных
пород на сжатие сж и растяжение р ;
модуль упругости -
E, Па;коэффициент Пуассона - ;
модуль сдвига G, Па.
Слайд 8Напряжения и деформации
Напряжение - величина векторная и зависит от величины
и направления действия силы, формы образца и внутренних свойств породы
Слайд 9F
N
T
A
Рассмотрим образец, на грань которого действует сила F. Ее можно
разложить на две составляющие:
нормальную N,направленную перпендикулярно рассматриваемой площадке
и касательную T, направленную параллельно этой площадке.
Слайд 10F - сила действующая на образец горной породы, Н.
N -
нормальная составляющая силы F. Направлена перпендикулярно рассматриваемой площадке, Н.
T -
касательная составляющая силы F. Направлена вдоль рассматриваемой площадке, Н.A - площадь образца на которую действует сила F, м2
Слайд 11напряжение
Это относительная величина равная по величине отношению действующей силы
к площади образца, на которой она действует
Слайд 12Нормальные напряжения
Нормальные напряжения действуют перпендикулярно площадкам ( сечению) и превращают
куб (квадрат) в параллелепипед, т.е. не меняют прямых углов.
Разрыв, растяжение,
сжатие
Слайд 13Касательные напряжения
Касательные напряжения действуют в плоскости сечения и превращают куб
в параллелограмм, т.е. изменяют прямые углы
Срез, сдвиг
Слайд 14Напряжения в системе СИ выражаются в паскалях (Па).
1 Н/м2 =
1 Па
Паска́ль (русское обозначение: Па, международное: Pa) — единица измерения давления (механического напряжения) в Международной системе единиц
(СИ).Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр:
1 Па = 1 Н·м−2.
С основными единицами СИ паскаль связан следующим образом:
1 Па = 1 кг·м−1·с−2.
Единица названа в честь французского физика и математика Блеза Паскаля. Впервые наименование было введено во Франции декретом о единицах в 1961 году
Слайд 15а - одноосное напряженное состояние;
б - плоское напряженное состояние;
в -
объемное напряженное состояние.
Слайд 16Схема напряжений, отнесенная к произвольной системе координат
X, Y, Z
В
общем случае на гранях бесконечно малого элемента могут действовать нормальные
и касательные напряжения
Слайд 17Тензор напряжений
Напряжения, действующие на гранях бесконечно малого параллелепипеда, можно записать
в виде таблицы, называемой тензором напряжений:
Слайд 18Нормальные напряжения снабжаются индексом, который указывает координатную ось, вдоль которой
направлено напряжение.
Из условия равновесия бесконечно малого параллелепипеда вытекает закон парности касательных
напряжений: касательные напряжения на взаимно-перпендикулярных площадках, направленные перпендикулярно линии пересечения этих площадок, равны по величине.Поэтому τyx=τxy; τzx=τxz; τyz=τzy
Слайд 19В любом поле напряжений можно найти такие направления осей координат,
при которых все касательные компоненты тензора оказываются равными нулю.
Слайд 23Нормальные напряжения 1, 2, 3 являются главными нормальными напряжениями, направления
их действия главными осями напряжений, а площадки, на которых они
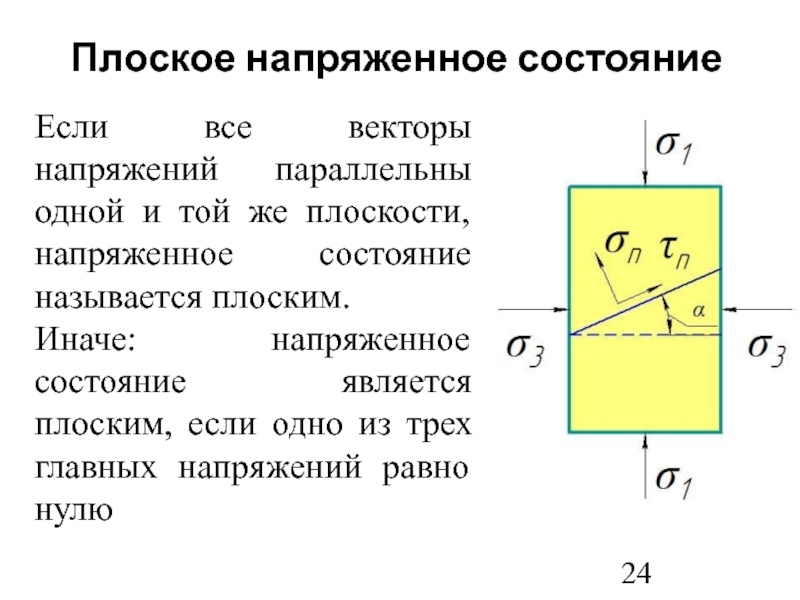
действуют, называются главными площадками напряжений.
Слайд 24Плоское напряженное состояние
Если все векторы напряжений параллельны одной и той
же плоскости, напряженное состояние называется плоским.
Иначе: напряженное состояние является
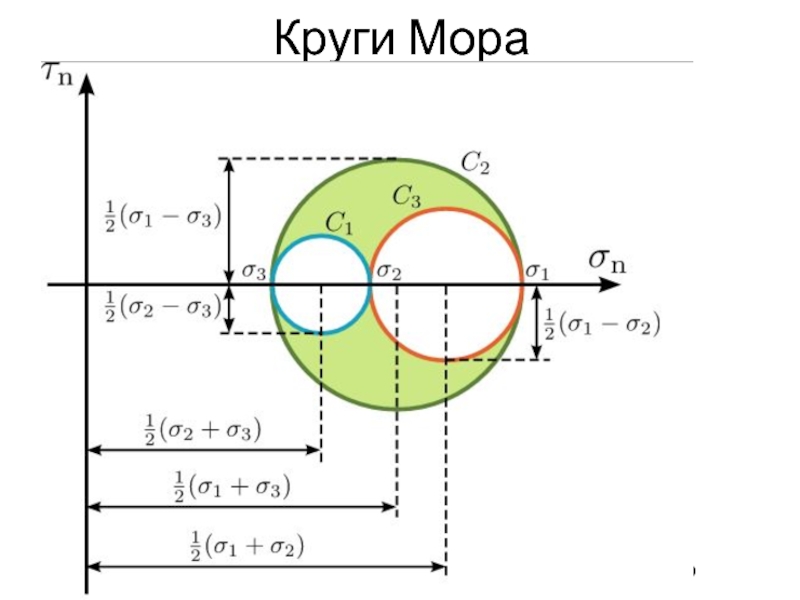
плоским, если одно из трех главных напряжений равно нулю
Слайд 25Напряженное состояние на любой площадке образца породы можно охарактеризовать действующими
на ней нормальным и касательным напряжениями.
Они взаимосвязаны и могут
быть представлены графически с помощью кругов Мора. 
Слайд 27Значения касательного и нормального напряжений в любой точке образца могут
быть найдены, если задан угол наклона плоскости, по которой определяются
напряжения. Под этим углом из точки пересечения круга с абсциссой проводится прямая линия до пересечения с окружностью.Координаты точки пересечения окружности с прямой линией численно равны значениям отыскиваемых напряжений.
Слайд 28В плоскости под углом к главным осям будут действовать
напряжения:
нормальные
n = 1 Cos2 + 3 Sin2
касательные
n =
0,5 (1 - 3) Sin 2
Слайд 30Практически же площадь, на которую воздействуют силы, представляет собой площадь
минеральных зерен и площадь, занятую порами. На площади, занятой порами,
напряжения не возникают, в результате чего напряжения концентрируются только в области контакта минеральных зерен.Поэтому с увеличением пористости - в равных условиях напряжения в породе возрастают.
Слайд 32Напряжения в породах могут возникать не только под действием внешних
сил, но и под действием различных физических полей.
Термические напряжения, возникают
в результате неравномерного распределения температуры при нагреве породы.Усадочные напряжения - при неравномерном охлаждении объема.
Остаточные напряжения - при неравномерном распределении напряжений из за текучести материала.
Эти напряжения носят названия собственных напряжений.
Собственные напряжения накладываются на внешние напряжения и могут либо увеличивать, либо уменьшать их.
Слайд 33Под действием внешних сил горная порода испытывает изменения линейных размеров,
объема или формы.
Все эти изменения носят название деформации
Слайд 35Линейные деформации
По направлению действующей силы деформации называются продольными, перпендикулярно ей
- поперечными.
L - изменение продольного размера образца (абсолютная продольная деформация).
D
- изменение поперечного размера образца (абсолютная поперечная деформация).
Слайд 36Эти деформации измеряются непосредственно в лабораторных опытах и называются абсолютными
деформациями.
Измеряют их с помощью: линейки, микрометра, специальных измерителей деформаций
и тензорезисторов.
Слайд 42Деформация образца породы под действием касательных () напряжений
δ
Сдвиг граней образца
под
действием касательных
напряжений
Слайд 43Деформация сдвига δ определяется по величине
tg
где - угол сдвига.
Так как
угол очень мал, то можно принять tg . 
Слайд 44Деформации, по действию, могут быть разрушающие и неразрушающие.
Разрушающие деформации вызывают
разделение породы на отдельные части.
Неразрушающие – вызывают изменение размеров и
формы образца породы без нарушения ее сплошности и могут быть пластическими или упругими.
Слайд 46В случае упругих деформаций наблюдается прямая зависимость между напряжением и
соответствующей деформацией
Максимальное напряжение, при котором еще не обнаруживаются остаточные деформации,
называется пределом упругости данной породы. 
Слайд 47Области деформации пород
Виды пород 1- упругая; 2 - пластическая;
1 - упруго-хрупкие (кварциты); 3 - разрушающая; 2 - упруго-пластичные (роговики); 3 - пластичные (мрамор).
Слайд 48Коэффициент пропорциональности между действующим продольным напряжением (растягивающим или сжимающим) и
соответствующей ему относительной деформацией называется модулем продольной упругости (модуль Юнга):
Па (Н/м).
Слайд 49Коэффициент пропорциональности между касательным напряжением и соответствующей ему относительной деформацией
сдвига носит название модуля сдвига:
Па (Н/м).
Слайд 50На практике часто пользуются еще одним упругим показателем пород -
коэффициентом Пуассона.
В отличие от всех предыдущих, упругих параметров, он
является коэффициентом пропорциональности только между деформациями - относительными продольными и относительными поперечными: 
Слайд 51В случае идеально упругих тел достаточно знать лишь модуль Юнга
и модуль сдвига, так как другие параметры могут быть вычислены
по определенным соотношениям теории упругости. Например, модуль сдвига:
Слайд 52В условиях равномерного упругого трехосного сжатия породы наблюдается прямая пропорциональная
зависимость между действующим давлением и относительным изменением объема породы:
Слайд 53Соответствующий коэффициент пропорциональности (К) называется модулем объемного (всестороннего) сжатия. Он
так же связан с модулем продольной упругости и коэффициентом Пуассона
зависимостью:
