Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика реального кристалла
Содержание
- 1. Физика реального кристалла
- 2. Упругие поля и напряжения вокруг дислокаций
- 3. Поле смещений вокруг винтовой дислокацииЦилиндрическиекоординаты:r, , zx2 + y2 = r2;tg = y/x uz = uz(x,y)
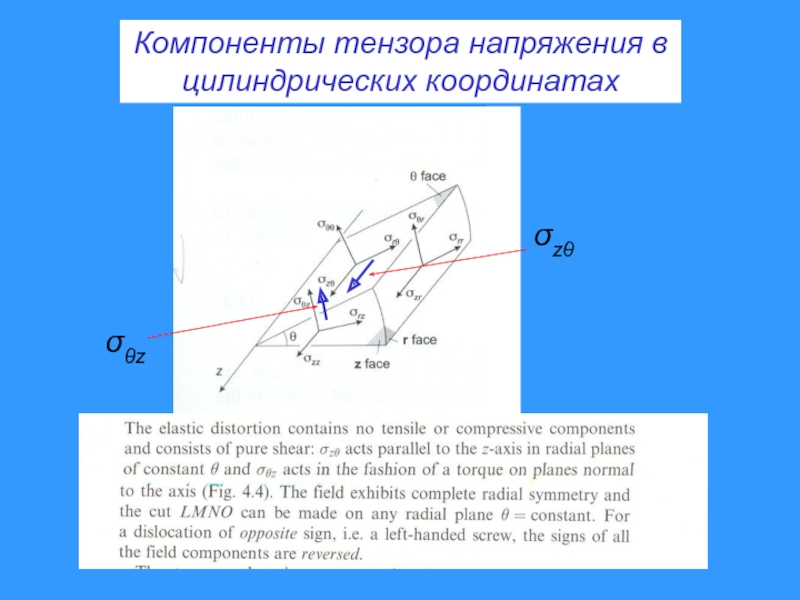
- 4. Компоненты тензоров напряжений и деформаций в цилиндрических координатахиспользуя соотношения:и, аналогичным образом, для сдвиговых деформаций, получаем:
- 5. Компоненты тензора напряжения в цилиндрических координатахzz
- 6. Отличные от нуля компоненты ij и kl
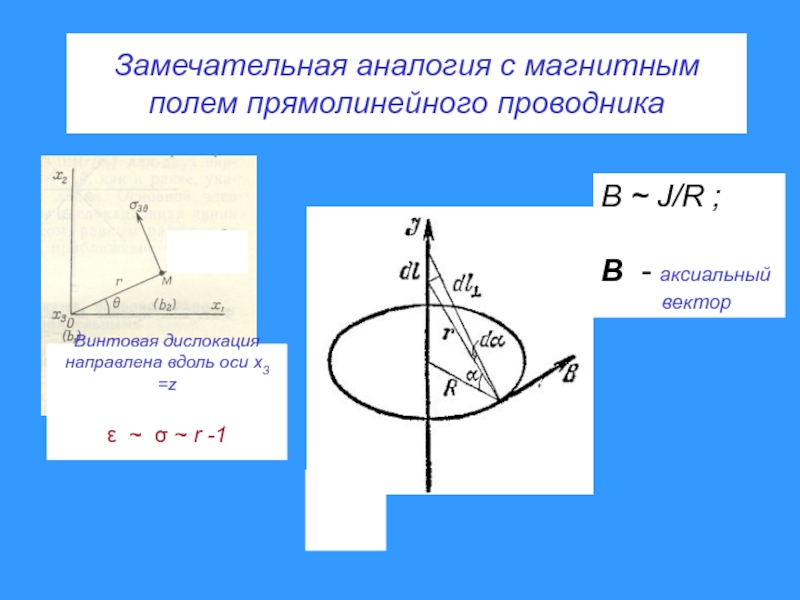
- 7. Замечательная аналогия с магнитным полем прямолинейного проводникаB
- 8. Электрическое поле равномерно заряженнойпрямолинейной нитиТеорема Гаусса – - Остроградского
- 9. Слайд 9
- 10. Упругая энергия дислокацииПолная энергия дислокации состоит из
- 11. Оценки упругой энергии дислокацииПри обычных значениях плотности
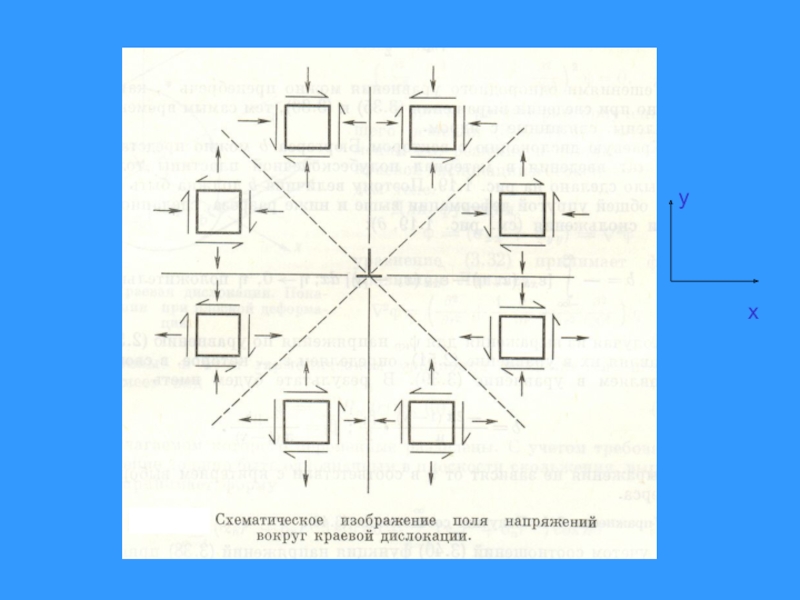
- 12. Поле напряжений прямой краевой дислокации(сплошная изотропная среда)Плоское
- 13. Вычисление компонент тензоров деформации и напряжений ux = ux(x,y)uy = uy(x,y)
- 14. Поля упругих смещений вокруг прямолинейной краевой дислокации
- 15. Слайд 15
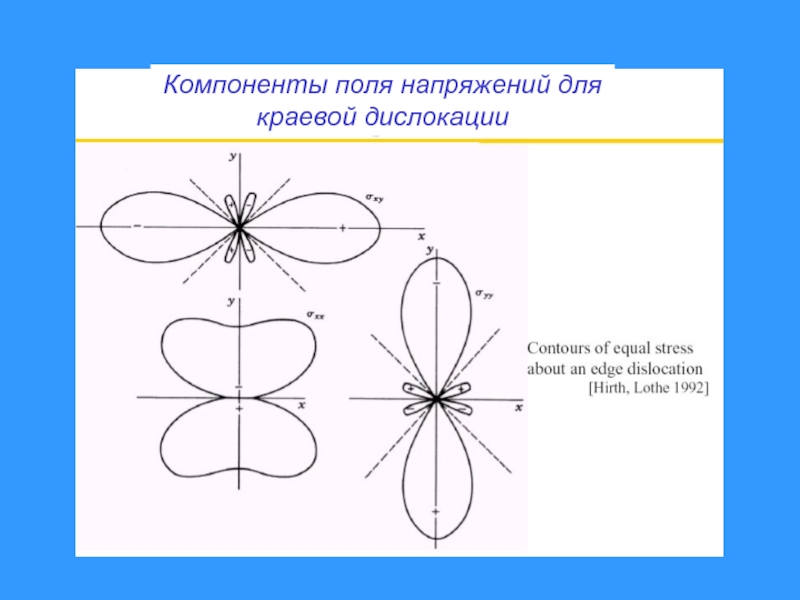
- 16. Компоненты поля напряжений для краевой дислокации
- 17. Компоненты тензора напряжений в случае винтовой дислокацииВывод:
- 18. Силы, действующие на дислокации
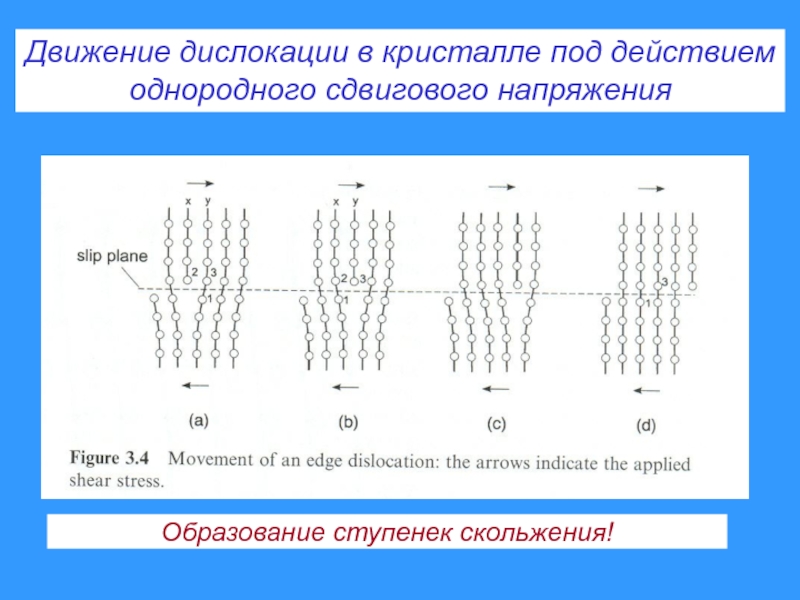
- 19. Образование ступенек скольжения!Движение дислокации в кристалле под действиемоднородного сдвигового напряжения
- 20. Сила, действующая на единицу длины дислокацииСила всегда направленаперпендикулярно линиидислокацииGj =biijвектор
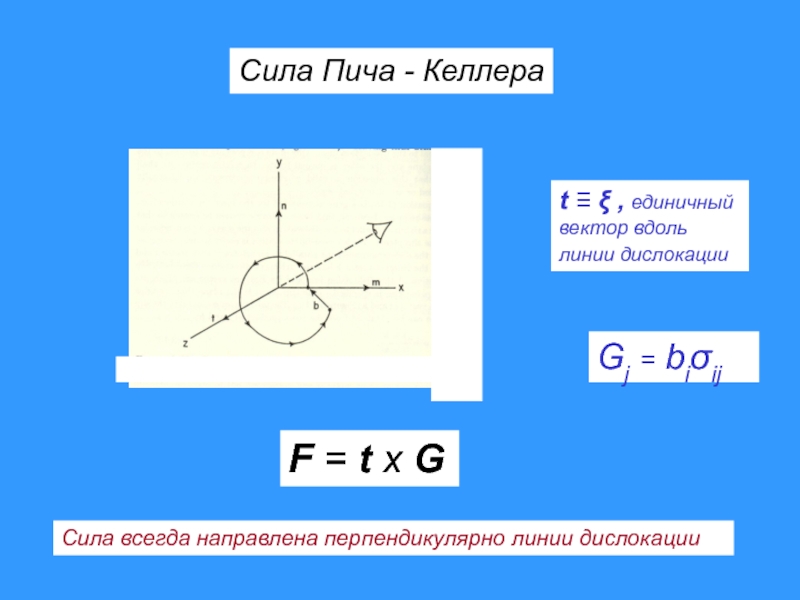
- 21. Формула Пича - Келлера(сила, действующая на единицу
- 22. Сила Пича - Келлераt ,
- 23. Сила Пича - Келлера
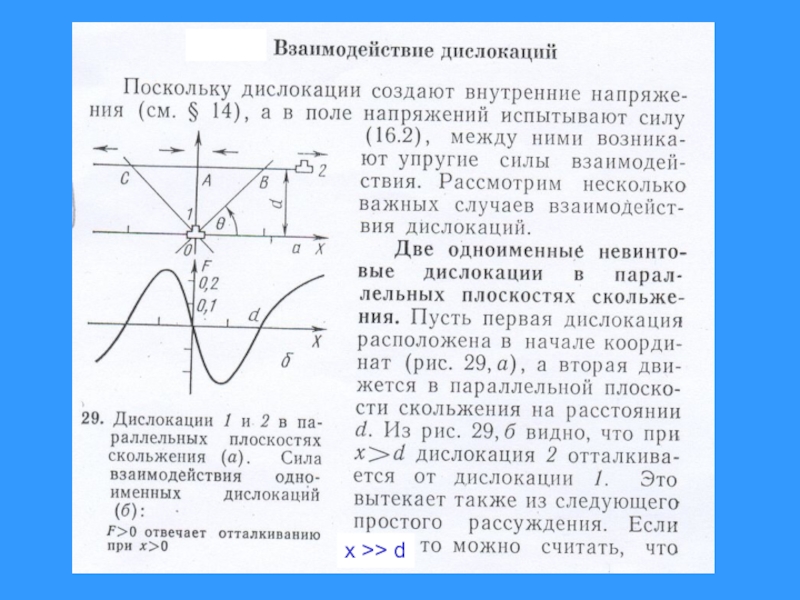
- 24. Взаимодействие дислокаций
- 25. Силы между дислокациями?Аналогия с заряженным конденсатором
- 26. Взаимодействие двух параллельных винтовых дислокаций
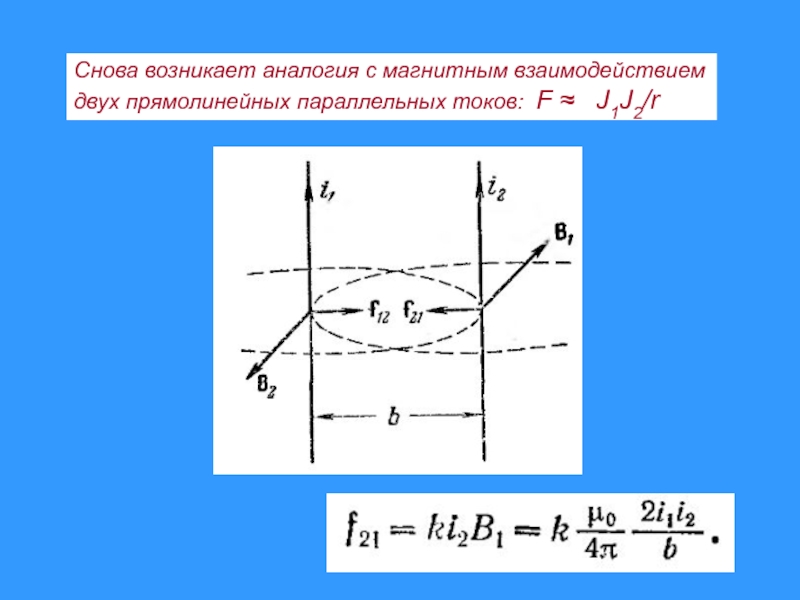
- 27. Снова возникает аналогия с магнитным взаимодействиемдвух прямолинейных параллельных токов: F J1J2/r
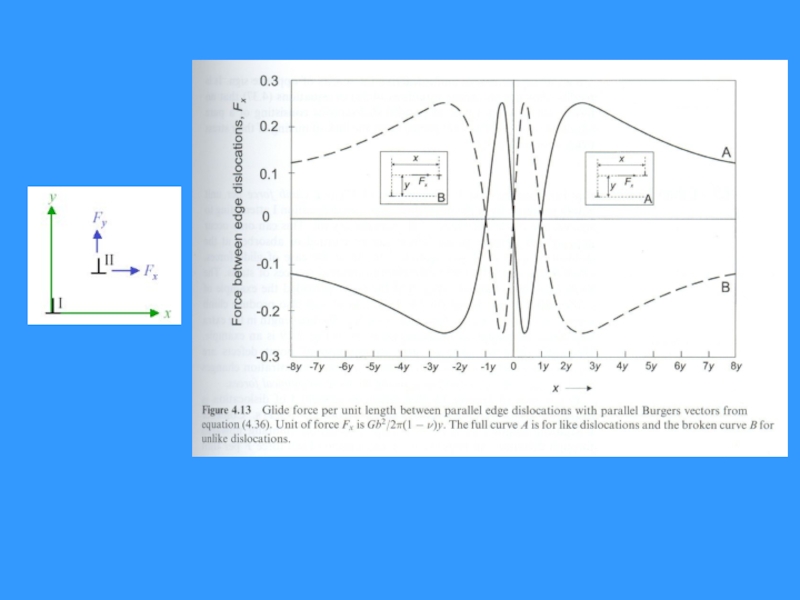
- 28. Взаимодействие двух параллельных краевых дислокаций
- 29. Вычисление сил взаимодействий
- 30. Слайд 30
- 31. Слайд 31
- 32. x >> d
- 33. Слайд 33
- 34. Стабильные конфигурации краевых дислокацийСтабильные дипольные конфигурации для дислокаций противо- положного знакаСтабильнаяконфигурациядля дислокаций одного знака
- 35. Слайд 35
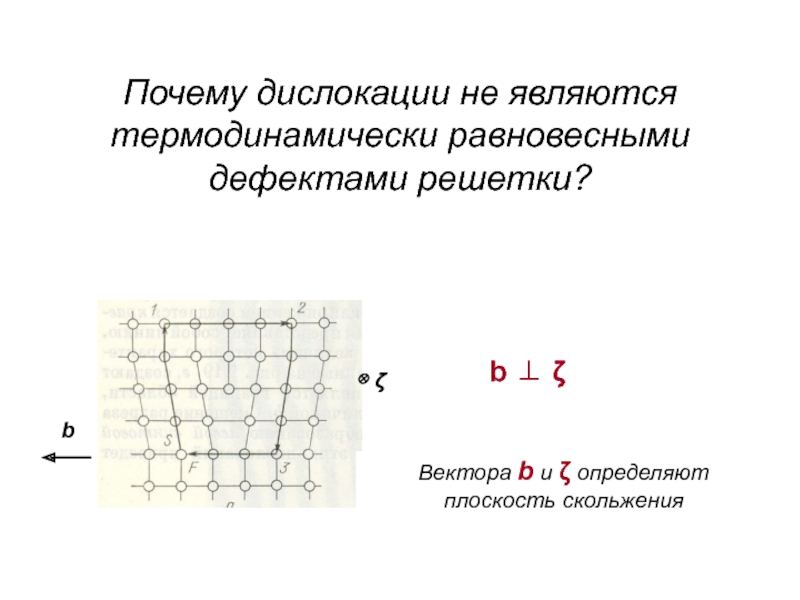
- 36. Почему дислокации не являются термодинамически равновесными дефектами
- 37. Оценки упругой энергии дислокацииПри обычных значениях плотности
- 38. Расчет энтропии дислокационной линииЛегко вычислить общее число
- 39. В случае дислокации, состоящей из N звеньев,
- 40. Слайд 40
- 41. Таким образом свободная энергия системыможет быть минимизирована
- 42. Равновесная концентрация точечных дефектов = CNn = N!/n!(N-n)!c = n/N e E/ kT
- 43. Слайд 43
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Профессор Б.И.Островский
Физика реального кристалла
ostr@cea.ru
8. Упругие поля (поля напряжений)
вокруг
дислокаций. Энергия дислокаций.
Слайд 3Поле смещений вокруг винтовой дислокации
Цилиндрические
координаты:
r, , z
x2 + y2 =
r2;
tg = y/x
uz = uz(x,y)
Слайд 4Компоненты тензоров напряжений и деформаций в
цилиндрических координатах
используя соотношения:
и, аналогичным
образом, для сдвиговых деформаций, получаем:
Слайд 6Отличные от нуля компоненты ij и kl убывают с
расстоянием
от дислокации как r -1,
r -1
Упругие поля искажений вокруг дислокаций
являются дальнодействующими!
Слайд 7Замечательная аналогия с магнитным полем прямолинейного проводника
B J/R ;
B
- аксиальный
вектор
Винтовая
дислокациянаправлена вдоль оси x3 =z
r -1
Слайд 10Упругая энергия дислокации
Полная энергия дислокации состоит из двух частей:
Плотность упругой
энергии, запасенной в дислокации:
2
2
8
Полная энергия, запасенная в полом цилиндре радиуса
R и длины L := (Gb2/82)dz d rdr/r2 =
0
0
L
2
R
r0
L
L
Или на единицу длины дислокации:
полн
полн
/L =
полн
=
dV
Слайд 11Оценки упругой энергии дислокации
При обычных значениях плотности дислокаций =107
см-2, среднее
расстояние между ними составляет R -1/2
3.10-4 см, что даетдля
10
и
полн
/L =
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
полн
/L =
4.10 -4 эрг/см
Что в пересчете на одну связь дает:
Ebond = 4.10 -4 эрг/см x 2.10 -8 см = 8.10-12 эрг 5 эв
Слайд 12Поле напряжений прямой краевой дислокации
(сплошная изотропная среда)
Плоское деформированное
состояние: uz
= 0
ux = ux(x,y)
uy = uy(x,y)
-1 < < 1/2
E
=2G (1+ )Слайд 17Компоненты тензора напряжений в случае
винтовой дислокации
Вывод: все энергетические оценки, выполненные
ранее
для винтовых дислокаций, остаются справедливыми и
для краевых дислокаций
-1 <
< 1/2Gb/2(1- )
Слайд 19Образование ступенек скольжения!
Движение дислокации в кристалле под действием
однородного сдвигового напряжения
Слайд 20Сила, действующая на единицу длины дислокации
Сила всегда направлена
перпендикулярно линии
дислокации
Gj =biij
вектор
Слайд 21Формула Пича - Келлера
(сила, действующая на единицу длины дислокации)
Сила всегда
направлена
перпендикулярно линии
дислокации
t , единичный
вектор вдоль
линии дислокации
Слайд 22Сила Пича - Келлера
t , единичный
вектор вдоль
линии дислокации
Gj = biij
Сила всегда направлена перпендикулярно линии дислокации
F = t
x G Слайд 27Снова возникает аналогия с магнитным взаимодействием
двух прямолинейных параллельных токов: F
J1J2/r
Слайд 34Стабильные конфигурации краевых дислокаций
Стабильные дипольные
конфигурации для
дислокаций противо-
положного
знака
Стабильная
конфигурация
для дислокаций
одного знака
Слайд 36Почему дислокации не являются термодинамически равновесными дефектами решетки?
b
Вектора
b и определяют
плоскость скольжения
b
Слайд 37Оценки упругой энергии дислокации
При обычных значениях плотности дислокаций =107
см-2, среднее
расстояние между ними составляет R -1/2
3.10-4 см, что даетдля
10
и
полн
/L =
При G 1012 дин.см-2 и b = 2.10 -8 см имеем:
полн
/L =
4.10 -4 эрг/см
Что в пересчете на одну связь дает:
Ebond = 4.10 -4 эрг/см x 2.10 -8 см = 8.10-12 эрг 5 эв
Слайд 38Расчет энтропии дислокационной линии
Легко вычислить общее число путей длины N
:
если каждый узел решетки имеет z соседей,
то число
различных возможностей на каждом шаге есть z-1, и общее число путей равно
= N = (z - 1)N
(сумма статистических весов всех
конфигураций, возможных в системе).
Энтропия S определяется всеми возможными конформациями цепи, которые начинаются в начале координат и заканчиваются за N шагов:
S = kBln = kBNln(z-1)
Двумерный случай, D=2, z = 4: S = kBNln3
«траектория» дислокационной
линии в плоскости скольжения
Слайд 39В случае дислокации, состоящей из N звеньев, ее свободную энергию
можно записать в виде:
F = NE - TS =
NE – kBTNln3или в пересчете на одну связь:
F/N = E – kBTln3
kB T = 1.4 10-16 эрг/К x 1200 К =1.6 10-13 эрг 10-1 эв
E = Ebond 5 эв .
E >> kB T
Таким образом, прирост энтропии благодаря создаваемому
дислокациями беспорядку, недостаточен, чтобы компенсировать
рост энергии дислокационной линии.
T Tmelt
Слайд 41Таким образом свободная энергия системы
может быть минимизирована только если все
дислокации удалены из кристалла.
Термодинамически равновесные дислокации не
могут существовать в
кристалле.Дислокации, в отличие от точечных дефектов,
являются линейными дефектами решетки. Это
топологическое отличие проявляется при подсчете
числа состояний и энтропии дислокаций.