Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приёмы быстрого устного счёта: метод или гениальность?
Содержание
- 1. Приёмы быстрого устного счёта: метод или гениальность?
- 2. 1. Актуальность темы и цели исследования 3.
- 3. В начальной школе очень большую часть учебного
- 4. Выяснить, можно ли научить любого быстрому счету
- 5. существуют ли люди, действительно быстро считающие, и
- 6. Феноменальный счётчик (устар.), супервычислитель (совр.) — человек, обладающий способностью
- 7. Альфред Бине выделил общие отличительные черты феноменальных
- 8. Чтобы проверить эффективность некоторых способов быстрого счета,
- 9. Примеры после объяснения:676:4=472:4=900:51200:5314*9274*914*1315*14исследование эффективностиПримеры после объяснения:676:4=472:4=900:51200:5314*9274*914*1315*14
- 10. Слайд 10
- 11. Применение приёмов быстрого счёта позволило улучшить лучший
- 12. Приёмы быстрого счёта – не гениальность. И
- 13. Да – как минимум чтобы рассчитать
- 14. Спасибо за внимание!
- 15. 1.феноменальные счётчики2.способы быстрого счёта3.счётчики-спортсменыВспомогательные слайды
- 16. феноменальные счетчикиЛюди-калькуляторы (mental calculators)
- 17. Зера Колберн (1804-1840), шт. Вермонт, США:В 6
- 18. Луи Флери (1893-1980, Франция), слепой от рождения:10
- 19. Иоган Захариас Дазе (1824-1861, Германия)С 3 лет
- 20. Карл Фридрих Гаусс (1777-1855, Германия)3 года –
- 21. Андре Мари Ампер (1775-1836, Франция)Получил домашнее образование
- 22. Герт Митринг (р. 1966, Германия)4 года –
- 23. Приемы быстрого счета
- 24. 1. Умножение в пределах от 10 до
- 25. Умножение на 9Приписать 0 и отнять исходное числоПример: 241*9=2410-241=2169Умножение НАТУРАЛЬНЫХ чисел
- 26. Герт Митринг разработал умножение на пальцах в
- 27. 1. Деление на 5,50,25: удобно помнить, что:X
- 28. Чемпионат Мира по устным вычислениям 2014 прошел
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21. Актуальность темы и цели исследования
3. Феноменальные счетчики
4. Способы
быстрого счета
5. Исследование эффективности способов быстрого счета
6. Счетчики-спортсмены
7. Выводы
план
Слайд 3В начальной школе очень большую часть учебного времени мы тратили
на развитие навыков устного счета. Да и сейчас, в пятом
классе, мы посвящаем этому время практически каждый день. А ведь мы могли это время потратить на что-то другое! Потому что:У нас есть компьютеры
Даже в мобильном телефоне встроен калькулятор
Человек не может обогнать компьютер по скорости счета
Так зачем же мы тратим время на устный счет?
нужно ли быстро считать в уме
Слайд 4Выяснить, можно ли научить любого быстрому счету или это врожденная
способность, которая либо есть у человека, либо ее нет.
Цель работы
Слайд 5существуют ли люди, действительно быстро считающие, и что значит «действительно
быстро»?
как эти люди достигли такой скорости счета?
как им пригодилось это
умение в жизни?можно ли научить быстро считать любого?
стоит ли учиться быстро считать?
Для достижения цели работы нам нужно выяснить
Слайд 6Феноменальный счётчик (устар.), супервычислитель (совр.) — человек, обладающий способностью к быстрому счёту,
выполняемому с помощью математических алгоритмов исключительно на основе визуальных представлений
без произнесения слов о выполняемых действиях и полученных результатахгениальность?
Слайд 7
Альфред Бине выделил общие отличительные черты феноменальных счетчиков:
отсутствие влияний наследственности
и среды, принадлежность по происхождению к бедной неимущей среде;
очень раннее
и всегда предшествующее обучению чтению и письму обнаружение счётной способности (в среднем в возрасте 8 лет);поглощение умственной деятельности упражнениями в действиях над числами;
дальнейшее развитие счётной способности при упражнении и быстрый её упадок в случаях неиспользования
гениальность?
Слайд 8Чтобы проверить эффективность некоторых способов быстрого счета, мы провели тестирование
в двух пятых классах
В рамках этого теста мы дали ученикам
8 примеров и зафиксировали лучший, худший и средний результат по скорости решенияЗатем мы ознакомили учеников со способами быстрого счета, применимыми к таким примерам, и дали решить еще по 8 аналогичных примеров уже с использованием этих приемов
исследование эффективности
Слайд 9Примеры после объяснения:
676:4=
472:4=
900:5
1200:5
314*9
274*9
14*13
15*14
исследование эффективности
Примеры после объяснения:
676:4=
472:4=
900:5
1200:5
314*9
274*9
14*13
15*14
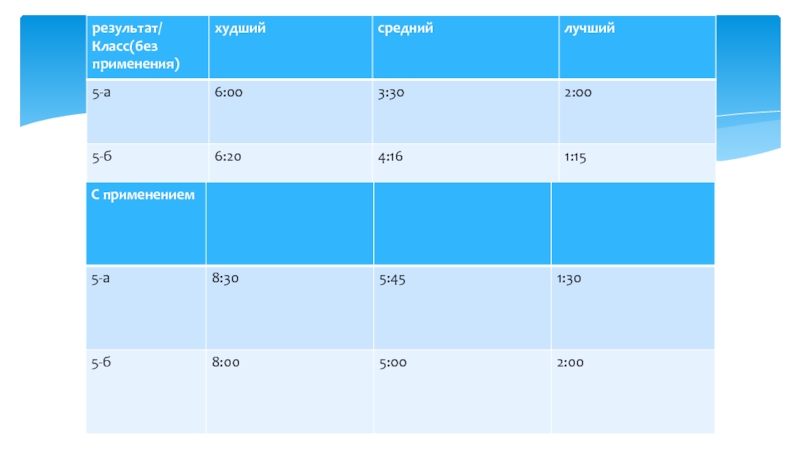
Слайд 11Применение приёмов быстрого счёта позволило улучшить лучший результат, но ухудшило
худший.
Худший и средний результаты с использованием приемов быстрого счета были
хуже, чем без их использования.Следовательно, приемы быстрого счета могут помочь только при условии тренировок в их применении, и они лучше и быстрее помогают тем, кто и без них имел хорошие способности к счету
В результате эксперимента выяснено:
Слайд 12Приёмы быстрого счёта – не гениальность. И быстрый счёт –
не гениальность. Быстрый счёт – полезная способность, которая не гарантирует
успеха, но может пригодиться в жизни. Приёмы быстрого счёта – упражнения позволяющие развить данную способность. Они как физкультура: чемпионом не сделают, но поддерживают в форме.вывод
Слайд 13 Да – как минимум чтобы рассчитать тормозной путь, когда
несёшься на своей «Феррари» со скоростью 200 км/ч. Калькулятор там
не поможет.Нужно ли уметь быстро считать в уме?
Слайд 17Зера Колберн (1804-1840), шт. Вермонт, США:
В 6 лет - умножил
в уме 12 225 на 1223. Отец Зеры эксплуатировал талант
сына, не давая ему толком учиться. В результате к моменту смерти отца (1822 год) способности Зеры к быстрым вычислениям угасли, он стал обычным человеком, хотя и выше среднего уровня.В 18 лет - стал учителем математики в школе, параллельно поступив учиться на священника.
В 31 год - стал профессором лингвистики.
гениальность?
Слайд 18Луи Флери (1893-1980, Франция), слепой от рождения:
10 лет – не
может одеваться, плохо ходит, не поддается обучению (в том числе
элементарной арифметике)15 лет – помещен в клинику для неизлечимо больных, где вскоре перенес сильный шок, увидев припадок другого больного. После перенесенного шока стал проявлять поразительные способности в устном счете, а также его мыслительная деятельность в целом нормализовалась
34 года - за 2 с умножал З-значное число на 2-значное и за 10с З-значное на З-значное
гениальность?
Слайд 19Иоган Захариас Дазе (1824-1861, Германия)
С 3 лет – способности к
арифметическим вычислениям
15 лет – выступает с демонстрацией своих способностей в
разных городахК 26 годам так и не освоил даже в минимальной степени ни одного иностранного языка, и даже элементарных концепций классической математики
В 1849 году он предложил Гамбургской академии наук составить таблицу факторов (возможных делителей) для всех чисел от 7 миллионов до 10 миллионов, и получил грант на эту работу
К моменту свой смерти Дазе составил эту таблицу для чисел между 7 и 8 миллионами, а также почти полностью следующий миллион
Гениальность?
Слайд 20Карл Фридрих Гаусс (1777-1855, Германия)
3 года – наблюдал за расчетами
отца с работниками, и нашел ошибку в вычислениях.
7 лет –
быстрее всех решал примеры в школе.1798-1808 гг. – десятилетие творчества и великих открытий: решил ряд задач, не поддававшихся другим ученым многие годы и даже тысячелетия; вычислил и указал место нахождения малой планеты – Цереры
30 лет – получает кафедру математики и астрономии в Геттингенском университете, а затем должность директора Геттингенской астрономической обсерватории
До конца жизни занимался исследованиями и достиг потрясающих результатов в области алгебры, геометрии, физики и астрономии
Гениальность?
Слайд 21Андре Мари Ампер (1775-1836, Франция)
Получил домашнее образование – вообще не
посещал школу
4 года – делает длинные вычисления в уме, пользуясь
правилами, которые узнал из игр в камешки13 лет – направил в Лондонскую академию наук несколько мемуаров по математике, в том числе серьезные замечания по трудам всемирно известного математика Эйлера
Был наделен феноменальной памятью и способностью у устному счету, но никогда не занимался развитием именно вычислительных способностей
1820 год – сделал сообщения об электромагнетизме, за которые его называют «Ньютоном электричества»
Гениальность?
Слайд 22Герт Митринг (р. 1966, Германия)
4 года – в магазине, пока
его мать складывала в корзинку выбранный товар, сообщил ей, сколько
нужно будет за всё заплатить12 лет - создал математические формулы, с помощью которых можно было установить, какой день недели соответствует той или иной дате на протяжении минувших четырёх тысяч лет
38 лет – извлек за 11,8 с корень 13-й степени из числа ниже:
706643738116724861022340088302401573757042331170702632731269721516000395709065419973141915549389684111
Написал несколько книг о приемах быстрого счета
К 2004 году защитил две докторские диссертации – в области математики и психологии
Гениальность?
Слайд 241. Умножение в пределах от 10 до 20: к одному
из чисел прибавляем количество единиц другого, сумму умножаем на 10
и прибавляем произведение единиц чисел. Пример:13*12=(13+2)*10+3*2=156
Умножение НАТУРАЛЬНЫХ чисел
Слайд 25Умножение на 9
Приписать 0 и отнять исходное число
Пример: 241*9=2410-241=2169
Умножение НАТУРАЛЬНЫХ
чисел
Слайд 26Герт Митринг разработал умножение на пальцах в пределах ста. Он
предлагает брать за основу круглое двухзначное число и изображать единицы:
пальцы вверх – нормальное число; пальцы вниз – отрицательное.Например: 33х33
Шаг 1: изобразить число 33. За основу берем 30 (т.к. это ближайшее число целых десятков).
На руках выставляем по 3 пальца вверх.
Шаг 2: возводим в квадрат число 30. 30х30=900
К этому числу прибавляем по 30 за каждый палец, и получаем
промежуточный результат: 30х30+30х6=1080
В заключение, прибавляем к промежуточному результату малый результат
(3х3=9), и получаем итог: 1080+9=1089
Умножение на пальцах
Слайд 271. Деление на 5,50,25: удобно помнить, что:
X : 5 =
X*2:10 X : 50= X*2:100 X : 25 = X*4:100
Пример: 125:5=125*2:10=25
2. Деление на 4,8: удобно помнить, что:
А:2:2=А:4
А:4:2=А:8
деление НАТУРАЛЬНЫХ чисел
Слайд 28Чемпионат Мира по устным вычислениям 2014 прошел 10/10/2014 - 12/10/2014
iна факультете математики в Дрезденском Университете Технологии в Германии.
39участников из
17 стран 5 основных видов состязаний:
Сложение десяти 10-значных чисел, 10 задач за 7 минут Победитель: Granth Thakkar (Индия); 10 правильных результатов за 242 секунды Умножение двух 8-значных чисел, 10 задач за 10 минут Победитель: Marc Jornet Sanz (Испания)), 10 правильных результатов за 295 секунд Вычисления календарных дат, 1 минута, даты вразброс за годы 600–2100 Победитель: Marc Jornet Sanz (Испания), 64 правильных результата Квадратные корни из 6-значных чисел, 10 задач за 10 минут Победитель: Rhea Shah (IИндия), 10 правильных результатов за135 seconds (каждый ответ вычислен до восьми знаков) Самый универсальный вычислитель (лучший счет за решение 5 заранее не объявленных типов задач) Победитель: Andreas Berger (Германия), 365/500 .
Чемпионат мира по устному счёту