Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика твердого тела Курс лекций (7) 1. Теория свободного электронного газа в
Содержание
- 1. Физика твердого тела Курс лекций (7) 1. Теория свободного электронного газа в
- 2. Модель движения электрона в потенциальном ящике получила
- 3. Если потенциальная энергия электрона равна нулю, то
- 4. Первые три энергетических уровня (штриховые линии) и
- 5. Для описания электронного газа необходимо выяснить, как
- 6. Введем обозначение:nF- квантовое число наивысшего занятого энергетического
- 7. Газ свободных электронов в трехмерном случае:Уравнение Шредингера
- 8. Компоненты волнового вектора k пробегают дискретный ряд
- 9. Определим импульс, действуя оператором импульса на волновую функцию. Скорость частицы с волновым вектором k равна:
- 10. Квантовые состояния системы из N свободных электронов
- 11. Тогда, если взять частное от деления всего
- 12. Радиус сферы Ферми зависит только от концентрации
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Модель движения электрона в потенциальном ящике получила дальнейшее развитие на
основе квантовой механики для описания свободного электронного газа.
Рассмотрим поведение
газа свободных электронов, находящихся в гипотетическом одномерном «кристалле», учитывая принципы квантовой механики. Движение электрона с массой m0 ограничено в этом случае прямой с длиной L, в начале и конце которой находятся потенциальные барьеры бесконечной высоты.
Волновая функция и энергетические уровни электрона могут быть получены из решения уравнения Шредингера:
Где Н – оператор Гамельтона (Гамельтонеан) –оператор полной энергии
где
-Оператор импульса.
Слайд 3Если потенциальная энергия электрона равна нулю, то
где
-Оператор импульса.
Или
где n
– энергия электрона в состоянии n;
Данному состоянию соответствует волновая функция
ψn.Граничные условия имеют вид:
Волновая функция, удовлетворяющая уравнению Шредингера и
граничным условиям имеет вид:
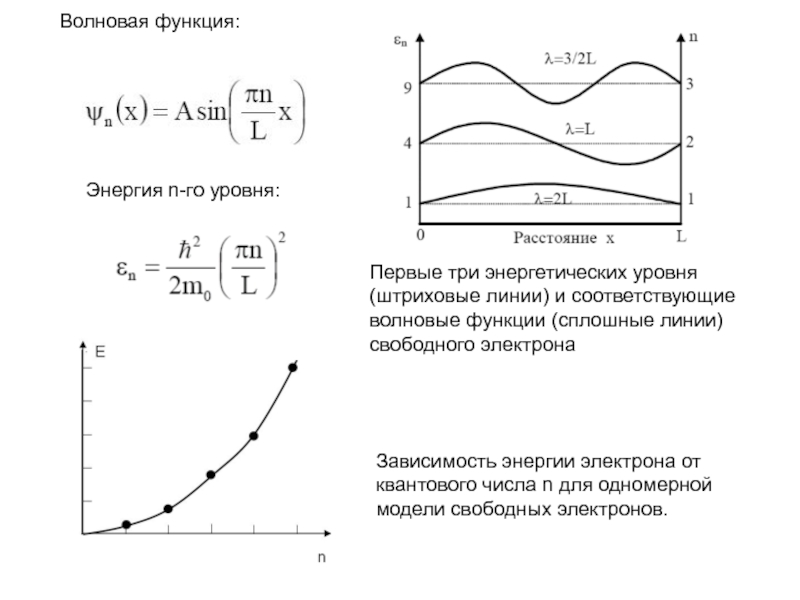
Слайд 4Первые три энергетических уровня (штриховые линии) и соответствующие
волновые функции (сплошные
линии) свободного электрона
Энергия n-го уровня:
Волновая функция:
Зависимость энергии электрона от квантового
числа n для одномерной модели свободных электронов. Слайд 5Для описания электронного газа необходимо выяснить, как распределены N электронов
по уровням энергии одномерного кристалла.
Электроны всегда подчиняются принципу Паули :
Никакие два электрона не могут иметь в этой системе одинаковые квантовые числа. (Свойство фермионов).
В одномерном твердом теле свободный электрон (электрон проводимости) имеет квантовые числа n и ms = ± . (n – целое, положительное число).
ms – спиновое квантовое число.
Слайд 6Введем обозначение:
nF- квантовое число наивысшего занятого энергетического уровня.
N – четное
число электронов (N = 2nF).
Будем последовательно заполнять электронами энергетические
уровни, начиная с низшего, (n =1), до N электронов по два электрона на уровень. Введем определение энергии электронов, соответствующей высшему заполненному уровню – энергии Ферми,
Для одномерной модели свободных электронов :
Слайд 7Газ свободных электронов в трехмерном случае:
Уравнение Шредингера имеет вид:
Решение уравнения
Шредингера будет иметь вид:
где nx, ny, nz – положительные целые
числа.Решение представляет собой плоскую волну.
Другая запись плоской волны имеет вид:
Слайд 8Компоненты волнового вектора k пробегают дискретный ряд значений:
Тем самым компоненты
волнового вектора k являются квантовыми числами
наряду со спиновыми квантовыми
числами.Собственные значения энергии электрона с волновым вектором k:
Слайд 9Определим импульс, действуя оператором импульса на волновую функцию.
Скорость
частицы с волновым вектором k равна:
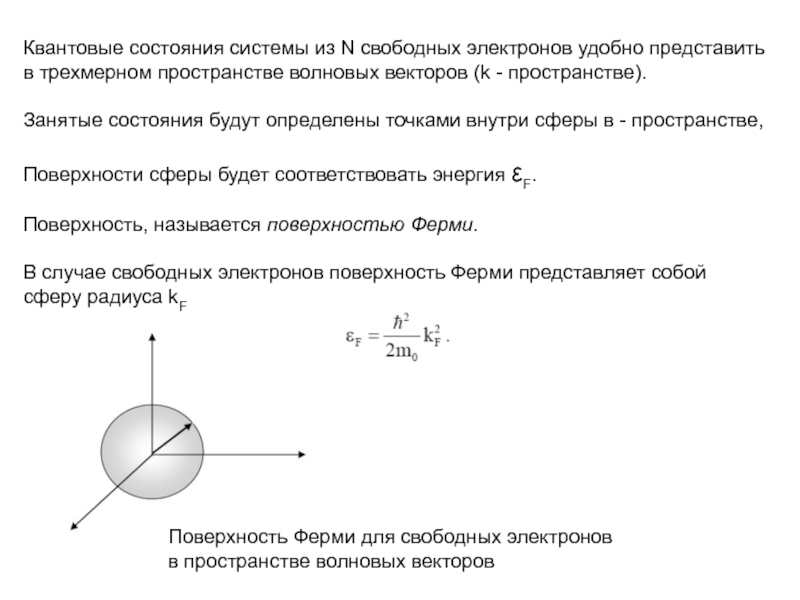
Слайд 10Квантовые состояния системы из N свободных электронов удобно представить в
трехмерном пространстве волновых векторов (k - пространстве).
Занятые состояния будут
определены точками внутри сферы в - пространстве, Поверхности сферы будет соответствовать энергия F.
Поверхность, называется поверхностью Ферми.
В случае свободных электронов поверхность Ферми представляет собой сферу радиуса kF
Поверхность Ферми для свободных электронов в пространстве волновых векторов
Слайд 11Тогда, если взять частное от деления всего объема k- пространства,
на элемент объема, соответствующий одному состоянию, то получим число состояний,
которое, должно быть равно половине числа электронов:(спиновое вырождение)
Пространство волновых векторов дискретно, так что каждому вектору K=(kx,ky,kz ) отвечает элемент объема в k - пространстве, равный величине:
- объем кристалла, тогда можно получить формулу радиуса сферы Ферми:
nэл – плотность электронов