Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика твердого тела Курс лекций 1 ВОЛНОВОЕ УРАВНЕНИЕ 2.Решение уравнения
Содержание
- 1. Физика твердого тела Курс лекций 1 ВОЛНОВОЕ УРАВНЕНИЕ 2.Решение уравнения
- 2. ВОЛНОВОЕ УРАВНЕНИЕ Для описания состояния
- 3. ВОЛНОВОЕ УРАВНЕНИЕ t – время, х
- 4. Для 3-х мерного случая волновое уравнение имеет
- 5. Шредингер преобразовал волновое уравнение для описания состояниямикрочастиц.
- 6. Для электронов волновая функция Ψ - это
- 7. Решение уравнения Шрёдингера для одномерного потенциального ящикаОдномерным
- 8. Обозначим Тогда уравнение Шредингера принимает вид
- 9. С учетом первого граничного условия получим:0 =или
- 10. Имеется и другой способ сохранения равенства.
- 11. ОтсюдаТаким образом, волновая функция описывается уравнением:Теперь вычислим энергию частицы. Поскольку Используя уравнение Шредингера Получаем:
- 12. Выводы по решению уравнения Шрёдингера:1. Энергия электрона
- 13. Решение уравнения Шрёдингера для трёхмерного потенциального ящика
- 14. Поделим левую и правую часть этого уравнения на (X.Y,Z):Полученное уравнение можно рассматривать как сумму трех уравнений:
- 15. Решение каждого из приведенных уравнений известно из
- 16. Выводы. 1. Энергия электрона квантована и принимает
- 17. Атом водорода В атоме водорода вокруг
- 18. Решение этого уравнения приводит к следующим основным
- 19. 3. Орбитальный
- 20. Решение уравнения Шрёдингера для атома водорода Имеет
- 21. Энергетические состояния атома водорода : Представленная комбинация квантовых чисел определяет энергию электрона
- 22. Форма атомных орбиталей
- 23. Строение многоэлектронных атомов1. В многоэлектронных атомах форма
- 24. Заполнение энергетических уровней происходит в соответствии с
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Физика твердого тела
Курс лекций
1 ВОЛНОВОЕ УРАВНЕНИЕ
2.Решение уравнения
Шрёдингера для одномерного потенциального ящика
ящикаСлайд 2 ВОЛНОВОЕ УРАВНЕНИЕ
Для описания состояния физического объекта требуется
указать
E – энергию тела, р – импульс, [x,y,z] –координаты.
Описание состояния твердого тела сводится к описанию состояния
составляющих его микрочастиц: атомов, ионов, электронов.
Атомы, ионы и электроны это – микрочастицы, находящиеся
в микрообъеме. Из-за присущего им свойства, описываемого
соотношением Гейзенберга (ΔрΔх h), возникает проблема
точного «механического» описания их состояния.
Австрийский физик Э.Шредингер (1926) предложил описывать состояние
микрочастиц волновой функцией, являющейся решением волнового
уравнения. Простейшее волновое уравнение имеет вид:
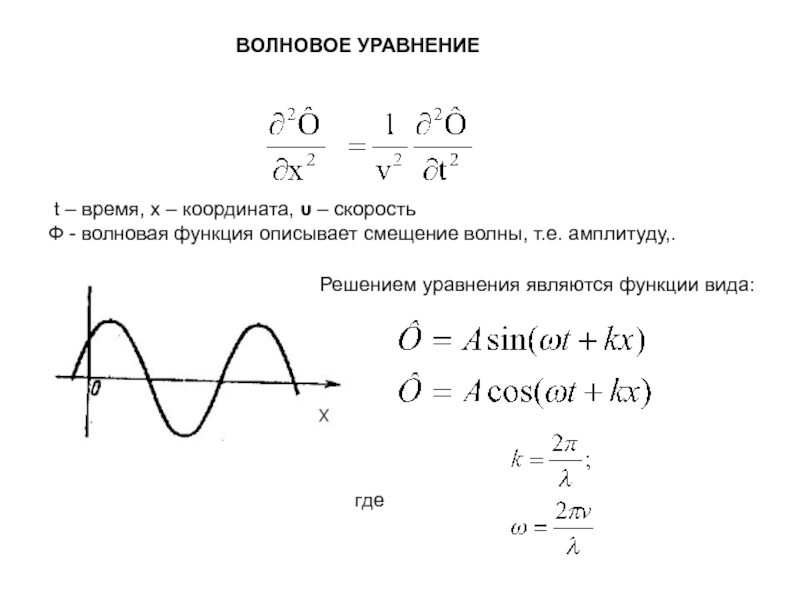
Слайд 3 ВОЛНОВОЕ УРАВНЕНИЕ
t – время, х – координата,
υ – скорость
Ф - волновая функция описывает смещение волны, т.е.
амплитуду,.Решением уравнения являются функции вида:
где
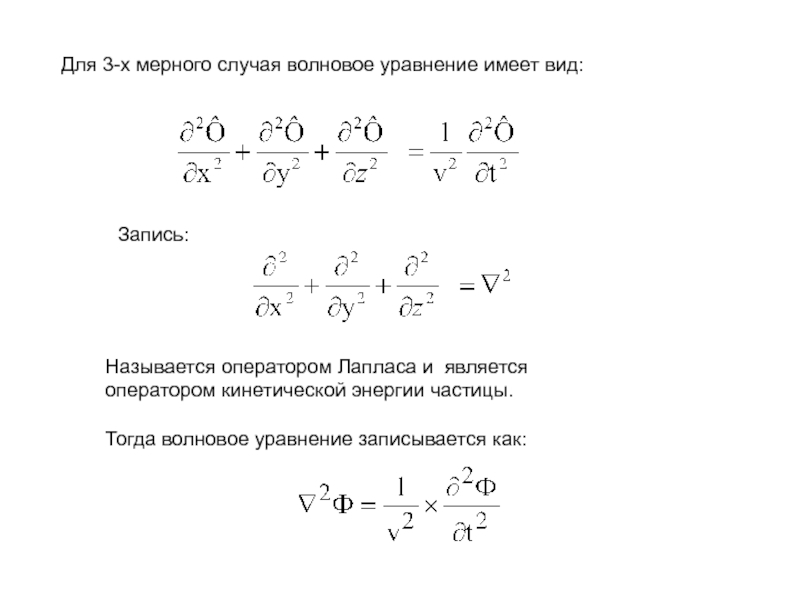
Слайд 4Для 3-х мерного случая волновое уравнение имеет вид:
Запись:
Называется оператором
Лапласа и является
оператором кинетической энергии частицы.
Тогда волновое уравнение записывается
как:Слайд 5Шредингер преобразовал волновое уравнение для описания состояния
микрочастиц. Для этого он
добавил в уравнение
(а)член учитывающий потенциальную энергию для стационарных систем,
(б) убрал член, описывающий изменение энергии во времени.
В результате получилось
Уравнение известное как уравнение Шредингера:
m – масса частицы
- Волновая функция
U –потенциальная энергия
E – полная энергия частицы.
Уравнение Шредингера является уравнением сохранения Энергии.
Первый член описывает кинетическую энергию,
Второй член - описывает кинетическую энергию,
Последний член – полную энергию.
Слайд 6Для электронов волновая функция Ψ - это не столько амплитудная
функция, сколько мера вероятности (вероятностная функция).
Квадрат амплитуды волновой функции
(x,y,z)2 выражаетотносительную плотность вероятности обнаружения частицы в точке
с координатами (х,y,z).
Решение уравнения Шрёдингера для атома водорода позволяет
определить волновые функции (x,y,z) и дискретные энергетические
уровни энергии электронов в атоме.
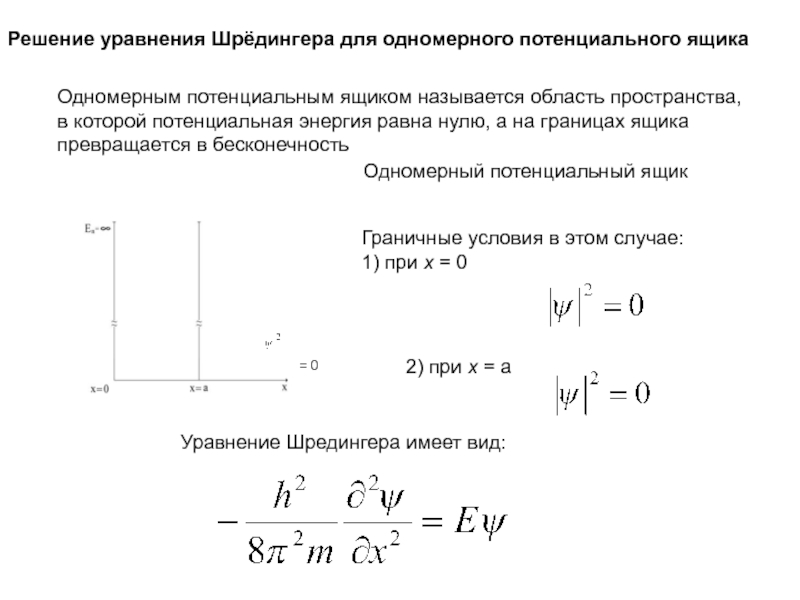
Слайд 7Решение уравнения Шрёдингера для одномерного потенциального ящика
Одномерным потенциальным ящиком называется
область пространства,
в которой потенциальная энергия равна нулю, а на границах
ящика превращается в бесконечность
Уравнение Шредингера имеет вид:
Одномерный потенциальный ящик
Граничные условия в этом случае:
1) при x = 0
2) при x = а
= 0
Слайд 8Обозначим
Тогда уравнение Шредингера принимает вид
.
Решением такого дифференциального уравнения в общем виде является функция
.
Действительно,
,
(
) =
Слайд 9С учетом первого граничного условия получим:
0 =
или 0 = А(0)+В(1).
Для
того, чтобы выполнялось это равенство, необходимо,
чтобы постоянная В была
равна нулю.Следовательно,
.
Учитывая, что при x = а, = 0 (второе граничное уравнение), получим
Это равенство справедливо при А=0.
Такое решение называется тривиальным, поскольку
обращает волновую функцию в ноль.
Слайд 10 Имеется и другой способ сохранения равенства.
Оно выполняется, очевидно,
при
, где п- целое число.
Тогда решение волнового уравнения принимает
вид:Постоянная А может быть определена из условия нормировки:
или
Слайд 11Отсюда
Таким образом, волновая функция описывается уравнением:
Теперь вычислим энергию частицы.
Поскольку
Используя уравнение Шредингера
Получаем:
Слайд 12Выводы по решению уравнения Шрёдингера:
1. Энергия электрона квантована и принимает
дискретные значения.
2. Энергия электрона определяется значением n – главного квантового
числа, 3. Вероятность нахождения электрона в той или иной области
потенциального ящика, определяется волновой функцией :
Зависит от значения квантового числа n.
4. Вероятности неодинаковы для разных точек пространства.
5. В некоторых точках вероятность равна нулю.
Такие точки называются узловыми.
Слайд 13Решение уравнения Шрёдингера для трёхмерного потенциального ящика
Трехмерный потенциальный ящик
имеет форму куба с ребром а.
Задача состоит в нахождении
волновой функции для уравнения: Разделим его на составляющие уравнения,
каждое из которых содержит только одну из координат.
С этой целью представим Е и Ψ в следующем виде:
После подстановки Е и в уравнение получим:
Слайд 14Поделим левую и правую часть этого уравнения на (X.Y,Z):
Полученное уравнение
можно рассматривать как сумму трех уравнений:
Слайд 15Решение каждого из приведенных уравнений известно из задачи
об одномерном
потенциальном ящике:
, где nx = 1,2,3 …;
, где ny
= 1,2,3 …;, где n z = 1,2,3 …
Для энергии и волновой функции получаем следующее выражения:
=
Слайд 16Выводы.
1. Энергия электрона квантована и принимает дискретные значения.
2. Волновая
функция электрона и его энергия определяется значениями
трёх квантовых чисел,
3. Количество квантовых чисел равно числу степеней свободы частицы.
4. Выводы 1-3 можно распространить на поведение электрона в более
сложных системах, например, электрона в атоме.
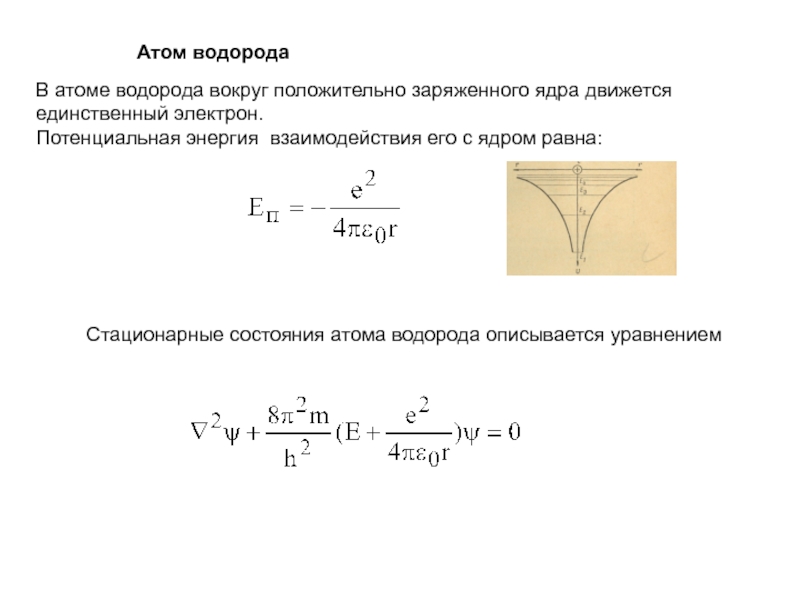
Слайд 17Атом водорода
В атоме водорода вокруг положительно заряженного ядра
движется
единственный электрон.
Потенциальная энергия взаимодействия его с ядром равна:
Стационарные
состояния атома водорода описывается уравнениемСлайд 18Решение этого уравнения приводит к следующим основным результатам.
Электрон в атоме
водорода обладает дискретным энергетическим спектром.
Собственные значения энергии определяются формулой:
где
-универсальная постоянная, n-главное квантовое число
2. Орбитальный момент количества движения pl может принимать лишь
следующий дискретный ряд значений:
,
где l побочное квантовое число.
Состояние с l=0 (при любом n) принято называть s-состоянием,
с 1=1 р-состоянием, с 1=2- d-состоянием, с 1=3— f-состоянием и т. д.
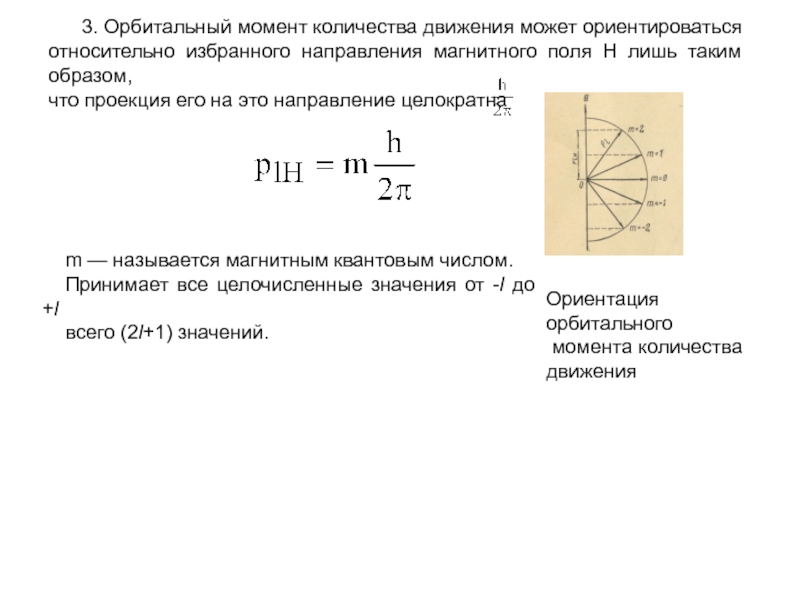
Слайд 19 3. Орбитальный момент количества движения
может ориентироваться
относительно избранного направления магнитного поля H лишь таким
образом, что проекция его на это направление целократна
m — называется магнитным квантовым числом.
Принимает все целочисленные значения от -l до +l
всего (2l+1) значений.
Ориентация орбитального
момента количества
движения
Слайд 20Решение уравнения Шрёдингера для атома водорода
Имеет три квантовых числа:
n - главное квантовое число, принимает целочисленные значения 1,2,3,4,…, n
L - побочное (орбитальное) квантовое число, принимающее
целочисленные значения от 0 до n - 1;
m - магнитное квантовое число, которое изменяться от –l до +l.
Обозначение волновых функций
l = 0 – s -орбитали;
l = 1 – p -орбитали;
l = 2 – d -орбитали;
l = 3 – f - орбитали.
l = 4- q - орбитали.
l = 5-h , q и h - орбиталями.
S- спиновое квантовое число s, принимает значения + 1/2 или -1/2.
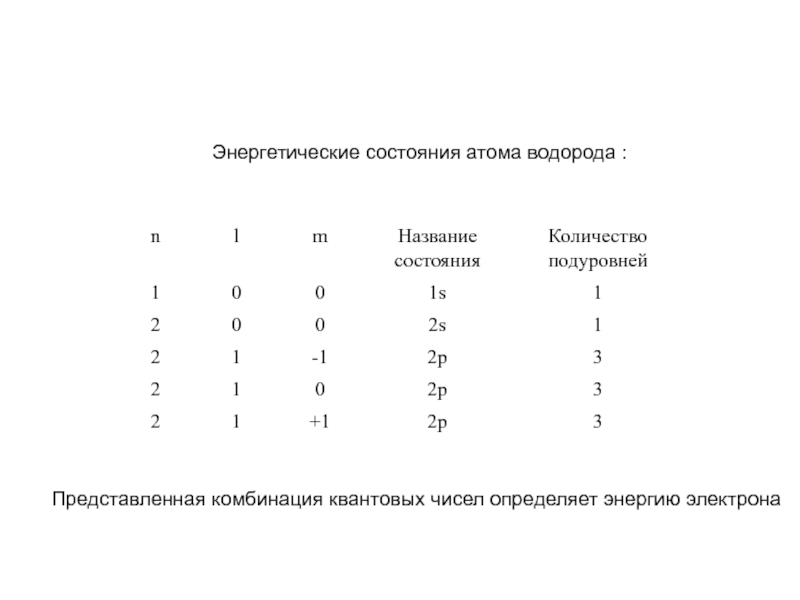
Слайд 21Энергетические состояния атома водорода :
Представленная комбинация квантовых чисел определяет
энергию электрона
Слайд 23Строение многоэлектронных атомов
1. В многоэлектронных атомах форма орбиталей, такая же,
как в атоме водорода.
2. Модель многоэлектронного атома можно построить
из последовательности водородоподобных орбиталей.
3. Последовательность определяется энергией орбиталей,
то есть значениями квантовых чисел n и l.
4. По сравнению с атомом водорода значительный вклад вносит число l,
что обусловлено двумя эффектами:
а. Эффект экранирования - действие ядра на электрон в многоэлектронном атоме
может ослабляться экранирующим действием внутренних электронных оболочек.
б. Эффект проникновения электрона к ядру (плотность е на ядре)
Наибольшую плотность имеют s электроны, затем p .
В связи с этим порядок возрастания энергии следующий:
1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s<5f=5d<6p<7s<7f
5d
Слайд 24
Заполнение энергетических уровней происходит в соответствии
с принципом Паули.
Принцип
Паули запрещает находиться в одном энергетическом состоянии более
чем двум
электронам с различными спинами. Другими словами, в атоме не может быть двух электронов с четырьмя
одинаковыми квантовыми числами. Или, в одном энергетическом состоянии
могут находиться лишь два электрона с разным спинами.
При не полном заполнении уровня характер заполнения электронов определяет также
правило Хунда.
электроны стремятся избегать одной и той же орбитали,
причём, расположенные на разных орбиталях электроны имеют одинаково
направленные спины.