Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формула Тейлора для функции нескольких переменных
Содержание
- 1. Формула Тейлора для функции нескольких переменных
- 2. Формула Тейлора для функции нескольких переменных. ТЕОРЕМА. Пусть
- 3. Доказательство. Точки, лежащие на отрезке М0М, имеют
- 4. Применяя правило нахождения производной сложной функции, получим:АналогичноПо индукции получим, что
- 5. Запишем для функции φ(t) формулу Тейлора с
- 6. ЗАМЕЧАНИЕ. При соблюдении условий теоремы имеет место также формула Тейлора с остаточным членом в форме Пеано:
- 7. Локальные экстремумы функции нескольких переменных. ОПРЕДЕЛЕНИЕ. Пусть
- 8. Необходимое условие экстремума.ТЕОРЕМА. Если в точке экстремума М0
- 9. ЗАМЕЧАНИЕ. Если в точке М0 функция f(М)
- 10. Достаточные условия экстремума. ТЕОРЕМА. Пусть функция f(M)
- 11. Так как по условию теоремы df(х0,y0) =
- 12. В нашем случае переменные связаны соотношением
- 13. СЛЕДСТВИЕ. Пусть z = f(x, y),
- 14. Слайд 14
- 15. ПРИМЕР. Исследовать на локальный экстремум функцию z =
- 16. Ее главные миноры равны:
- 17. Спасибо за внимание!misis.ru
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 4.5
Формула Тейлора для функции нескольких переменных.
Локальный экстремум функции нескольких
переменных, условия его существования и методы поиска.
Слайд 2Формула Тейлора для функции нескольких переменных.
ТЕОРЕМА.
Пусть функция z =
f(x, y) имеет в окрестности точки M0(х0,y0) непрерывные производные до
n-ого порядка включительно. Тогда для любой точки M(х, y) из этой окрестности справедлива формула Тейлора с остаточным членом в форме Лагранжа:
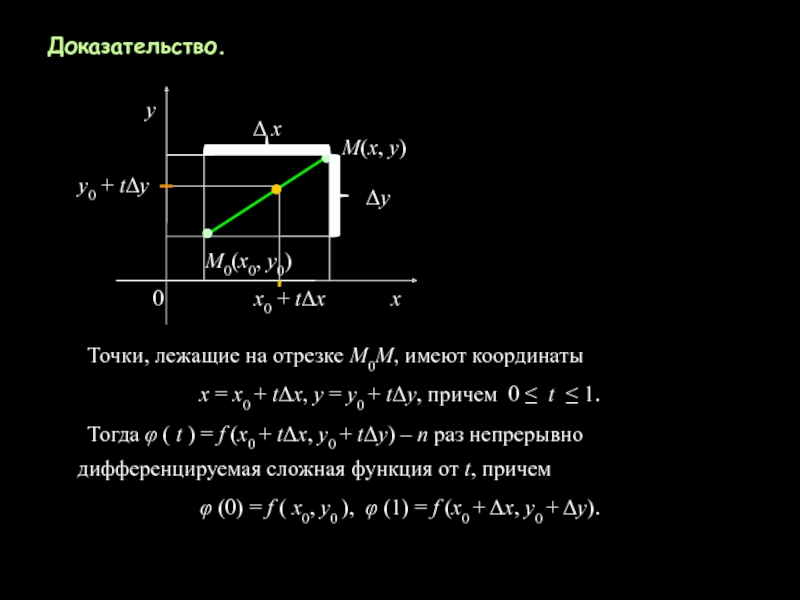
Слайд 3Доказательство.
Точки, лежащие на отрезке М0М, имеют координаты
х =
х0 + tΔx, y = y0 + tΔy, причем 0
≤ t ≤ 1.Тогда φ ( t ) = f (х0 + tΔx, y0 + tΔy) – n раз непрерывно дифференцируемая сложная функция от t, причем
φ (0) = f ( х0, y0 ), φ (1) = f (х0 + Δx, y0 + Δy).
Слайд 4 Применяя правило нахождения производной сложной функции, получим:
Аналогично
По индукции получим, что
Слайд 5 Запишем для функции φ(t) формулу Тейлора с остатком в форме
Лагранжа:
Полагая t = 1, получим
Заметим, что
Итак
Слайд 6 ЗАМЕЧАНИЕ.
При соблюдении условий теоремы имеет место также формула Тейлора
с остаточным членом в форме Пеано:
Слайд 7Локальные экстремумы функции нескольких переменных.
ОПРЕДЕЛЕНИЕ.
Пусть функция u =
f(х1, х2, ... хm) определена в области G⊂ Rm. Точка
М0∈G называется точкой локального максимума (минимума) функции f(М), если найдется такая δ-окрестность точки М0, что для всех точек М, принадлежащих этой окрестности, выполнено неравенствоf(М) – f(М0) ≤ 0 ( ≥ 0).
ПРИМЕР.
Слайд 8Необходимое условие экстремума.
ТЕОРЕМА.
Если в точке экстремума М0 функции f(М) существует
частная производная по какой-либо переменной, то эта производная равна нулю.
Доказательство.
Докажем теорему для функции двух переменных f(x, y).
Пусть М0(х0, у0) – ее точка локального экстремума. Пусть существует, например, fx (х0, у0). Введем вспомогательную функцию
ϕ (x) = f (x, у0).
Точка х0 является ее точкой экстремума, следовательно по теореме Ферма
ϕ ′(x0) = fx (х0, у0) = 0 ,
ч.т.д.
СЛЕДСТВИЕ.
Если в точке экстремума М0 функция f(М) дифференцируема, то
df(М0) = 0.
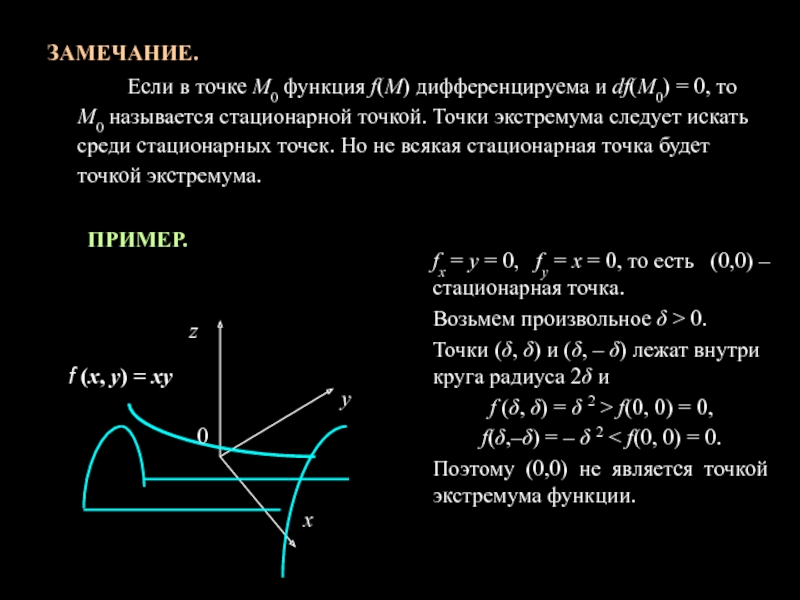
Слайд 9ЗАМЕЧАНИЕ.
Если в точке М0 функция f(М) дифференцируема и df(М0)
= 0, то М0 называется стационарной точкой. Точки экстремума следует
искать среди стационарных точек. Но не всякая стационарная точка будет точкой экстремума.ПРИМЕР.
fx = y = 0, fy = x = 0, то есть (0,0) – стационарная точка.
Возьмем произвольное δ > 0.
Точки (δ, δ) и (δ, – δ) лежат внутри круга радиуса 2δ и
f (δ, δ) = δ 2 > f(0, 0) = 0,
f(δ,–δ) = – δ 2 < f(0, 0) = 0.
Поэтому (0,0) не является точкой экстремума функции.
Слайд 10 Достаточные условия экстремума.
ТЕОРЕМА.
Пусть функция f(M) имеет в окрестности
точки M0 непрерывные частные производные второго порядка и пусть df(M0)
= 0. Тогдаесли d2f(M0) – положительно (отрицательно) определенная квадратичная форма, то M0 – точка локального минимума (максимума),
если d2f(M0) – неопределенная квадратичная форма, то M0 не является точкой экстремума.
Доказательство.
Приведем доказательство для функции двух переменных f(x, y).
По формуле Тейлора второго порядка с остаточным членом Пеано имеем
Слайд 11 Так как по условию теоремы df(х0,y0) = 0 , то
полное приращение функции в критической точке
Пусть для определенности d2f(M0) –
положительно определенная квадратичная форма. Тогдапри всех значениях , не равных нулю одновременно.
Слайд 12 В нашем случае переменные связаны соотношением
и поэтому одновременно
не равны нулю. Квадратичная форма
– непрерывная функция двух переменных,
принимающая только положительные значения и заданная на окружности радиуса 1 с центром в начале координат. Поскольку эта окружность есть компакт, то функция достигает на нем своей точной нижней грани m. Таким образом для всех значений аргументов, удовлетворяющих условию ( * ), а
Следовательно в достаточно малой окрестности точки М0 выполняется неравенство f(M) – f(M0) > 0, то есть М0 – точка локального минимума.
Слайд 13СЛЕДСТВИЕ.
Пусть z = f(x, y), M0(х0, у0) –
стационарная точка этой функции. Исследуем второй дифференциал функции в стационарной
точкеВоспользуемся критерием Сильвестра знакоопределенности квадратичной формы. В нашем случае
Возможные возникающие здесь ситуации сведем в таблицу:
Слайд 15 ПРИМЕР.
Исследовать на локальный экстремум функцию
z = x3 + 3xy2
– 39x – 36y + 26.
Найдем частные производные первого порядка
zx = 3x2 + 3y2 – 39; zy = 6xy – 36.
Для нахождения стационарных точек функции получим систему уравнений:
M1(3, 2), M2(– 3, – 2), M3(2, 3), M4(–2, –3).
Вычислим второй дифференциал функции
d2f(x, y) = 6xdx2 +2⋅6ydxdy + 6xdy2.
Матрица квадратичной формы в данном случае имеет вид: