Слайд 1ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ЛЕКЦИЯ 1
Слайд 22ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Слайд 37Частные производные функции нескольких переменных
Слайд 38 Частные производные
Для наглядности, здесь и далее все
определения и утверждения будем формулировать для функции 2-х (или 3-х)
переменных. На случай большего числа неизвестных они обобщаются естественным образом.
Пусть z = f(x,y) , D(z) = D xOy ,
Пусть M0(x0,y0)D .
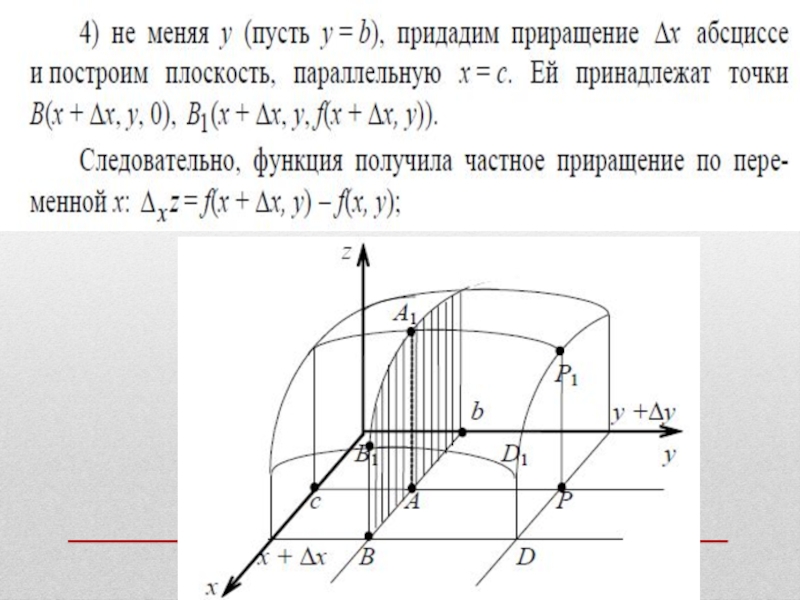
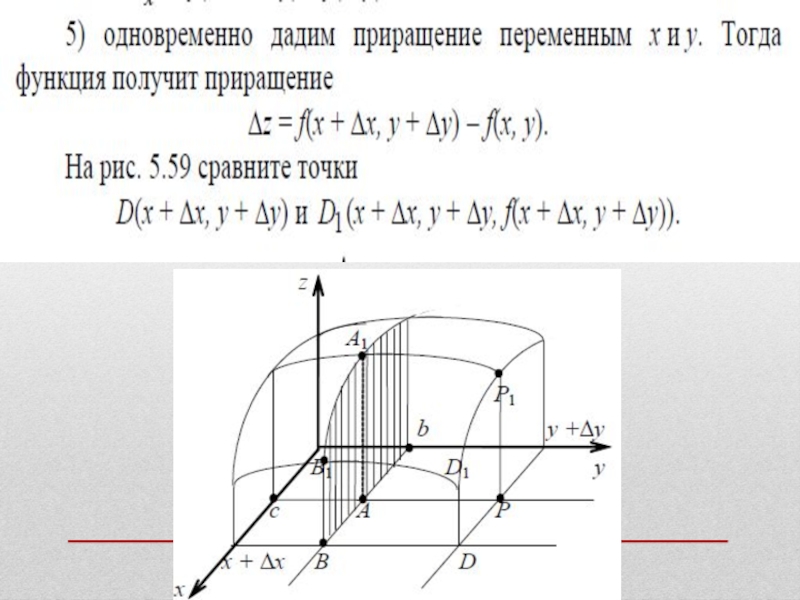
Придадим x0 приращение x, оставляя значение y0 неиз-
мененным (так, чтобы точка M(x0 + x,y0)D).
При этом z = f(x,y) получит приращение
xz(M0) = f(M) – f(M0) = f(x0 + x,y0) – f(x0,y0).
xz(M0) называется частным приращением функции
z = f(x,y) по x в точке M0(x0,y0).
Слайд 39ОПРЕДЕЛЕНИЕ. Предел при x 0 отношения
(если он существует и конечен)
называется частной производной функции z = f(x,y) по переменной x в точке
M0(x0,y0).
Обозначают:
или
Слайд 40Замечания.
1) Обозначения
и
надо понимать как целые символы, а не как частное двух величин. Отдельно взятые выражения z(x0,y0) и x смысла не имеют.
2) характеризует скорость изменения функции z = f(x,y)
по x в точке M0(x0,y0) (физический смысл частной производной по x).
Аналогично определяется частная производная функции z = f(x,y) по переменной y в точке M0(x0,y0):
Обозначают:
(и )
является функцией, определенной на D1(D2) D(f).
Ее называют частной производной функции z = f(x,y) по переменной x (y) и обозначают
Операция нахождения для функции z = f(x,y) ее частных производных
называется дифференцированием функции z = f(x,y) по переменной x и y соответственно.
– это обыкновенная про-
изводная функции z = f(x,y), рассматриваемой как функция одной переменной x (соответственно y) при постоянном значении другой переменной.
Поэтому, вычисление частных производных производится по тем же самым правилам, что и для функции одной переменой. При этом, одна из переменных считается константой.
Слайд 49ГЕОМЕТРИЧЕСКИЙ СМЫСЛ частных производных функции ДВУХ ПЕРЕМЕННЫХ.
Пусть функция z = f(x,y)
имеет в M0(x0,y0) частную произ-
водную по x (y).
Пусть поверхность
S – график функции z = f(x,y).
Тогда
где () – угол наклона к оси Ox(Oy) касательной, проведен-
ной в точке P0(x0,y0, f(x0,y0)) к линии пересечения поверхнос-
ти S и плоскости y = y0 (x = x0).
