Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гармонические колебания
Содержание
- 1. Гармонические колебания
- 2. План лекции
- 3. Определение:Колебания, которые совершаются по закону синуса или косинуса называются гармоническими.
- 4. Свободные или собственные колебанияКолебания, совершаемые под действием
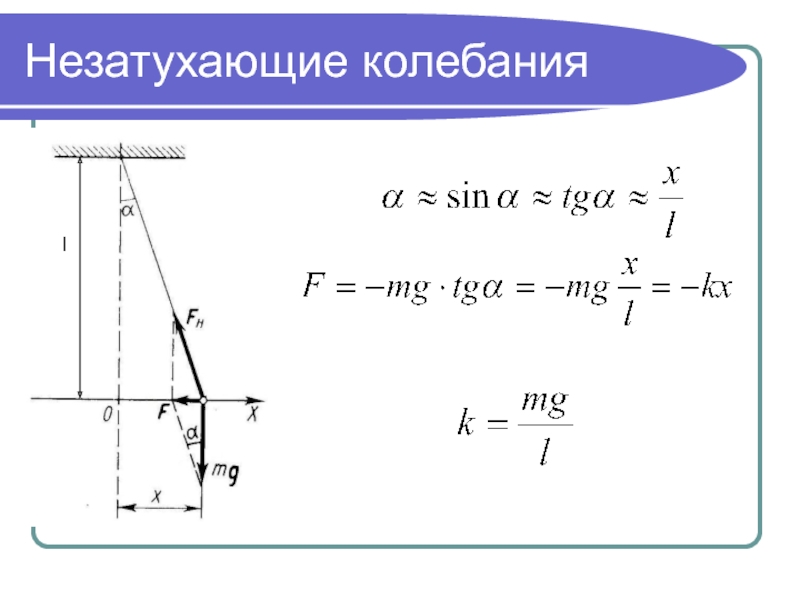
- 5. Незатухающие колебанияl
- 6. Квазиупругая силаСилы, неупругие по природе, но аналогичные
- 7. Дифференциальное уравнение незатухающих колебаний
- 8. Решениеили
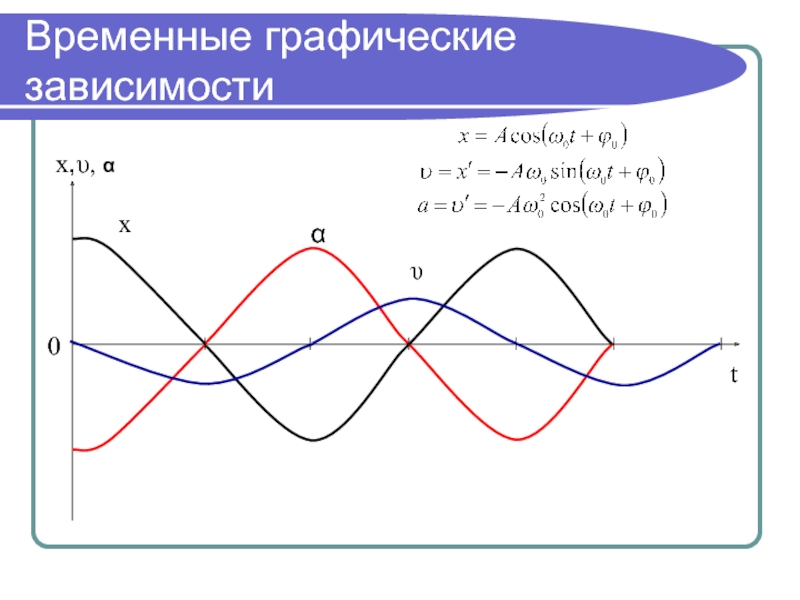
- 9. Временные графические зависимости x,υ, αtxαυ0
- 10. Затухающие колебания
- 11. Дифференциальное уравнение затухающих колебанийβ – коэффициент затухания; ω0 – круговая частота собственных колебаний системы.
- 12. Решение
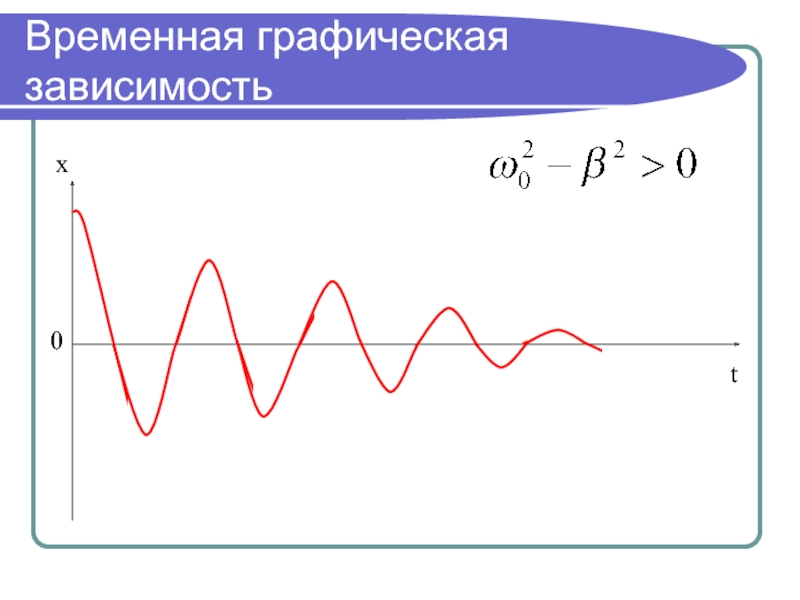
- 13. Временная графическая зависимостьxt0
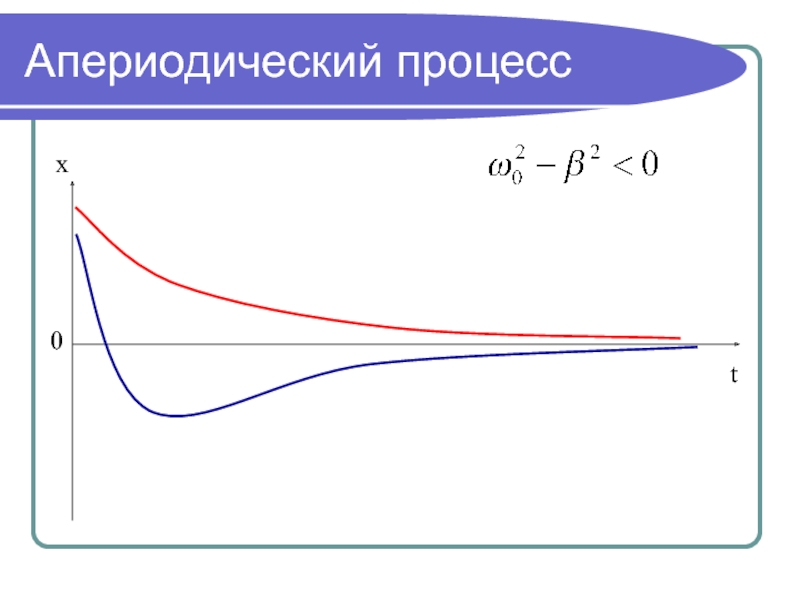
- 14. Апериодический процесс xt0
- 15. Логарифмический декремент затухания Величина, численно равная натуральному
- 16. Вынужденные колебания Вынужденными колебаниями называются такие колебания,
- 17. Дифференциальное уравнение вынужденных колебаний или
- 18. РешениеСумма колебаний с амплитудой
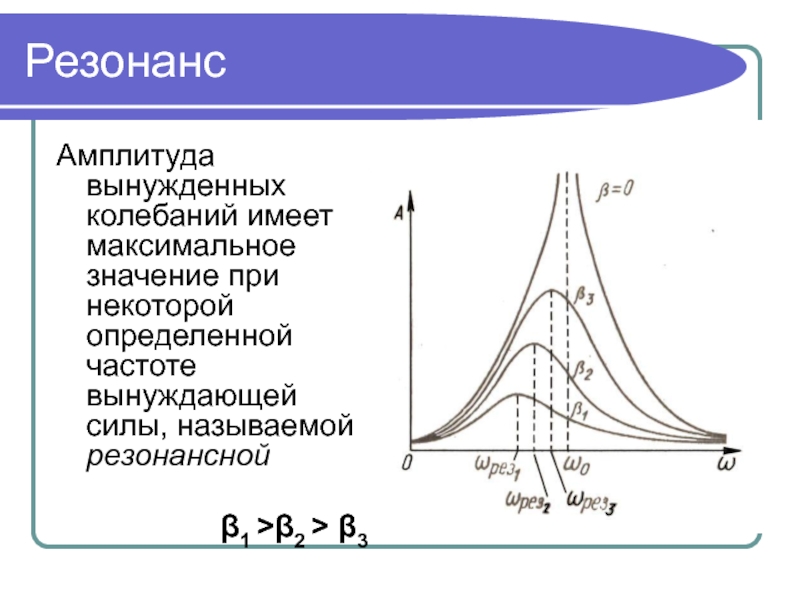
- 19. РезонансАмплитуда вынужденных колебаний имеет максимальное значение при
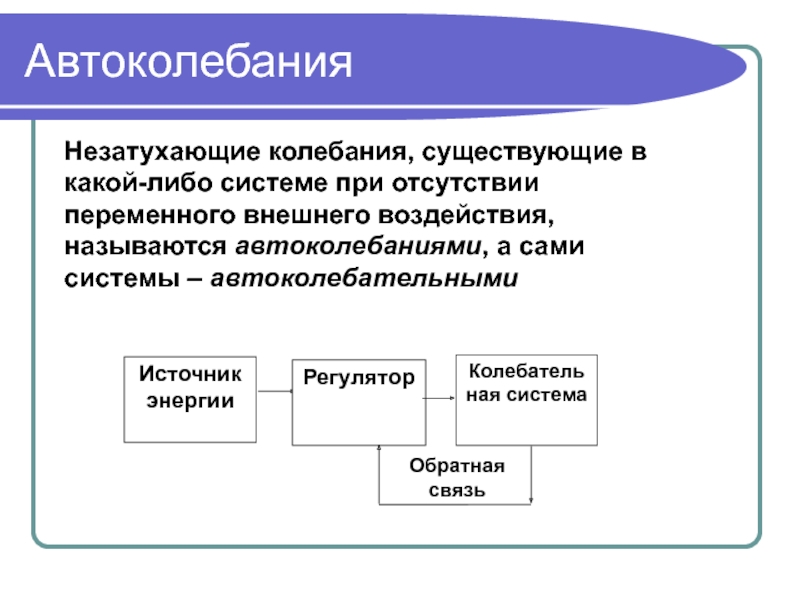
- 20. Автоколебания Источник энергииРегуляторКолебательная системаОбратная связьНезатухающие колебания, существующие
- 21. Кинетическая и потенциальная энергии незатухающего колебательного движения
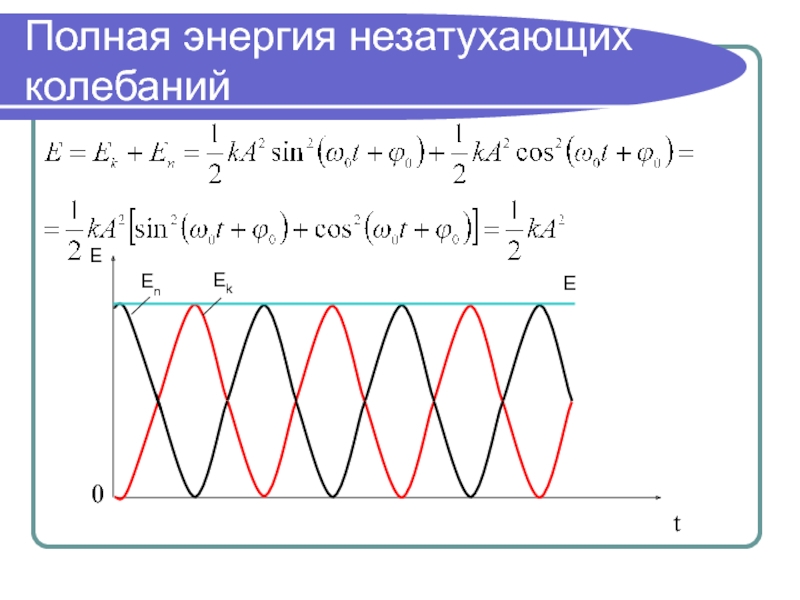
- 22. Полная энергия незатухающих колебанийt0EE
- 23. Сложение колебаний
- 24. Сложение гармонических колебаний, направленных по одной прямой
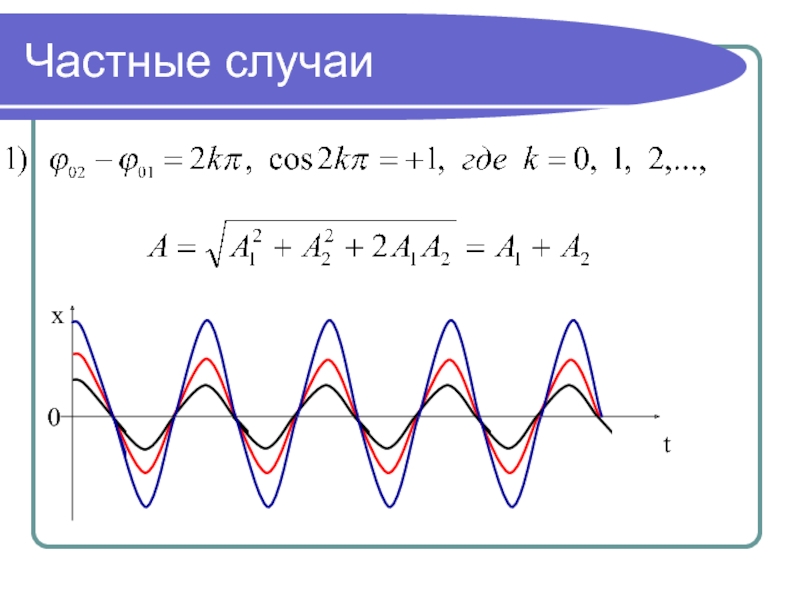
- 25. Частные случаиxt0
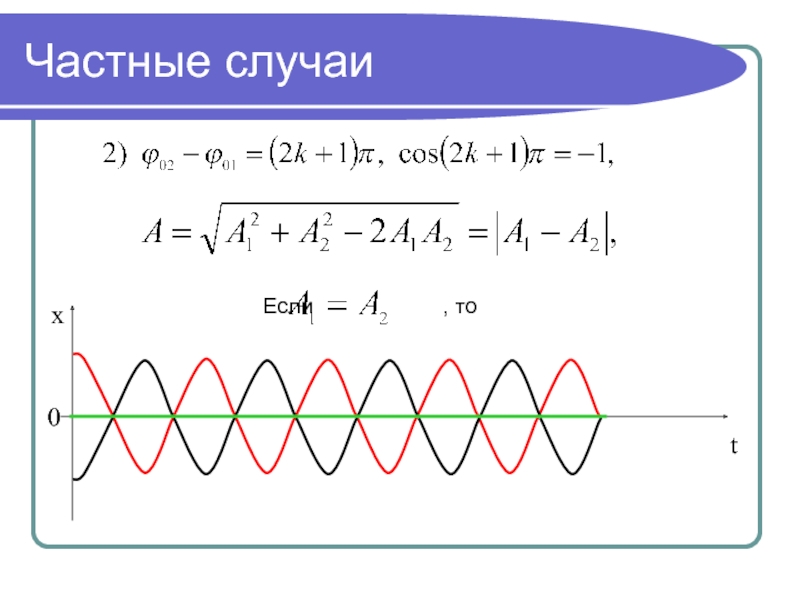
- 26. Частные случаиxt0Если
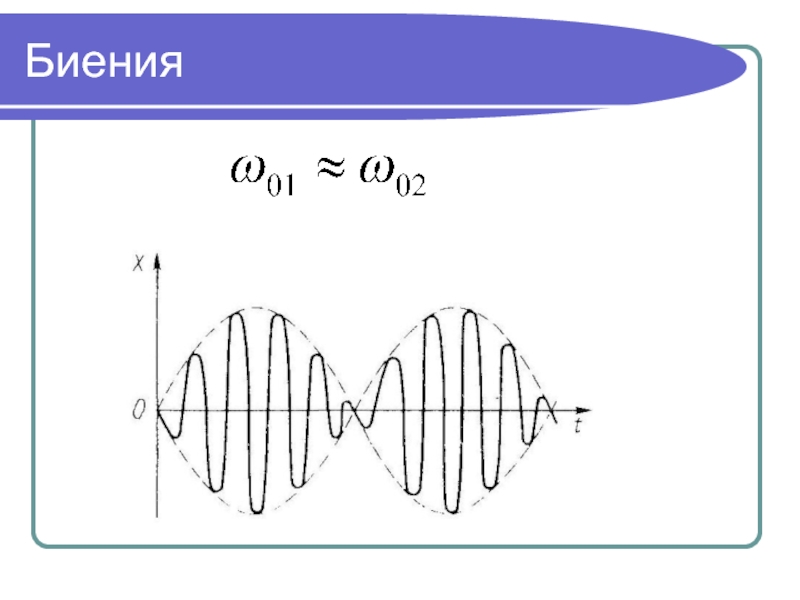
- 27. Биения
- 28. Сложение взаимно перпендикулярных гармонических колебаний
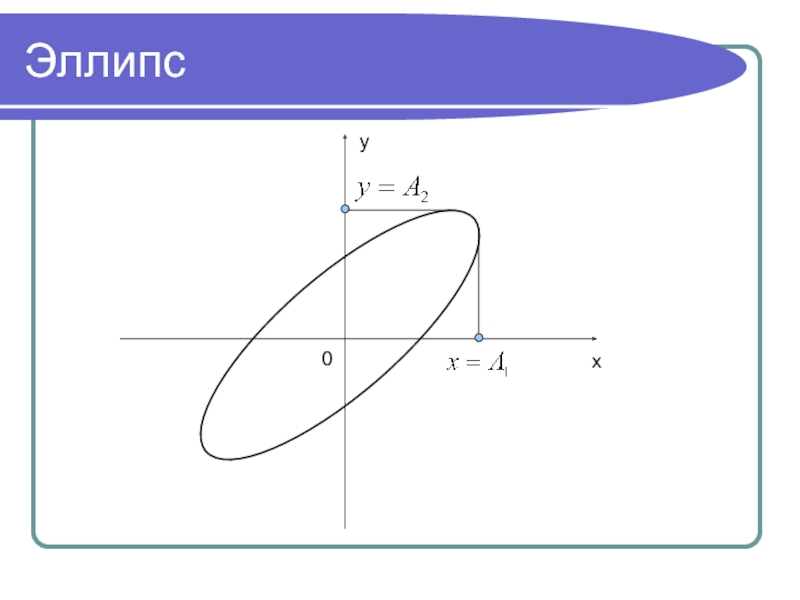
- 29. Эллипсyx0
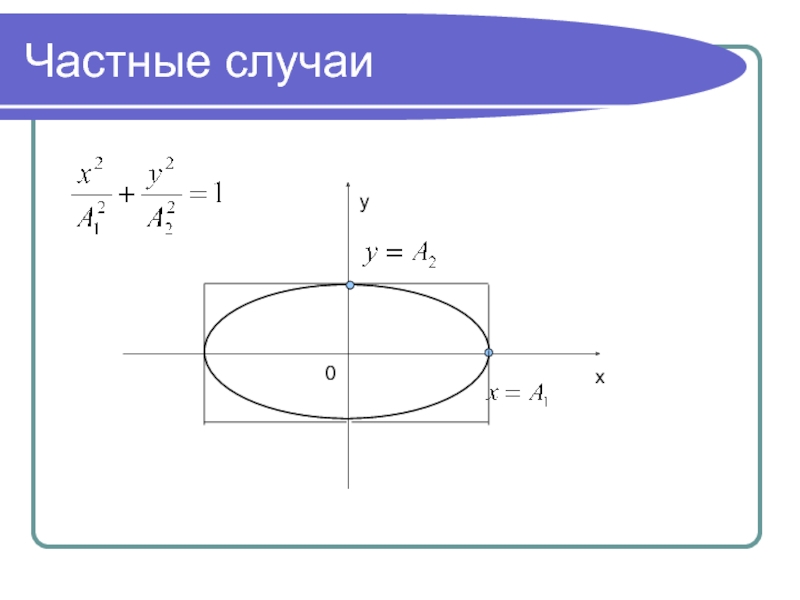
- 30. Частные случаи
- 31. Частные случаиyx0
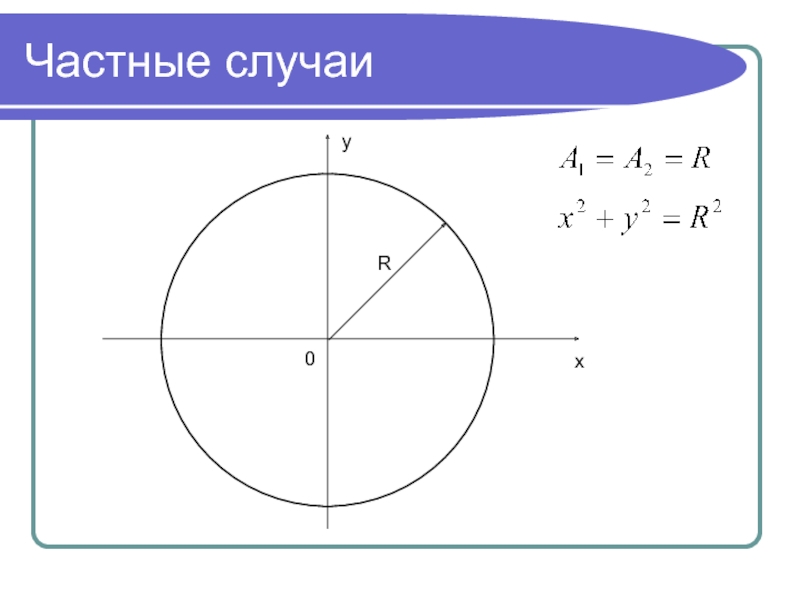
- 32. Частные случаиyx0R
- 33. Частные случаии тогда
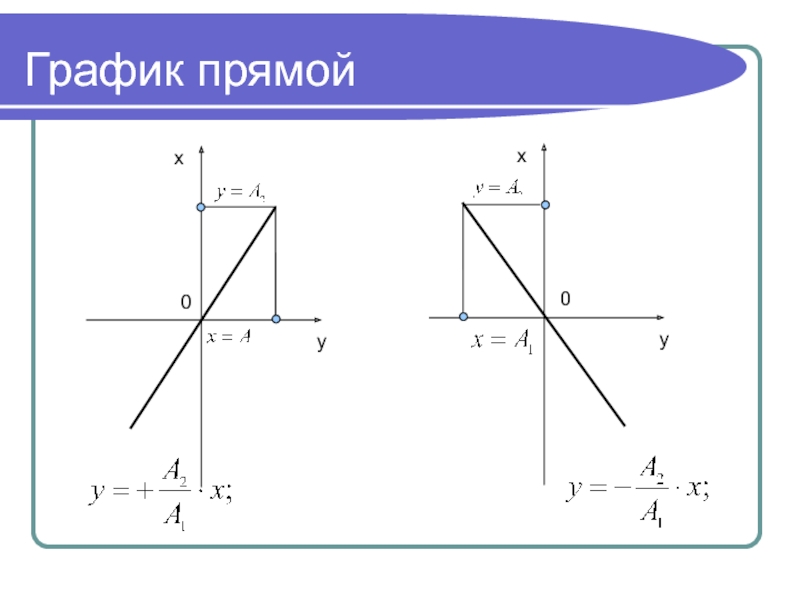
- 34. График прямой xy0xy0
- 35. Фигуры Лиссажу В зависимости от отношения частот и разности начальных фаз слагаемых колебаний
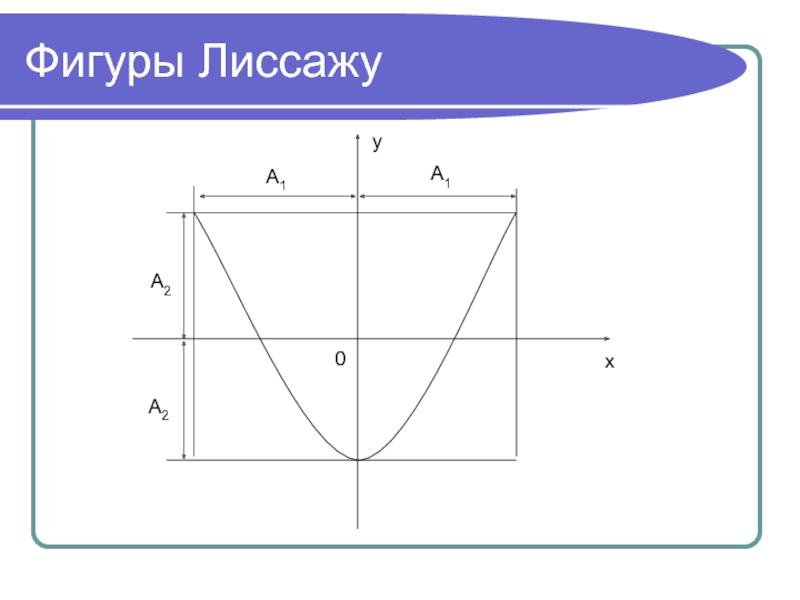
- 36. Фигуры Лиссажуyx0A1A1A2A2
- 37. Сложение колебаний. Гармонический спектр сложного колебания Фурье
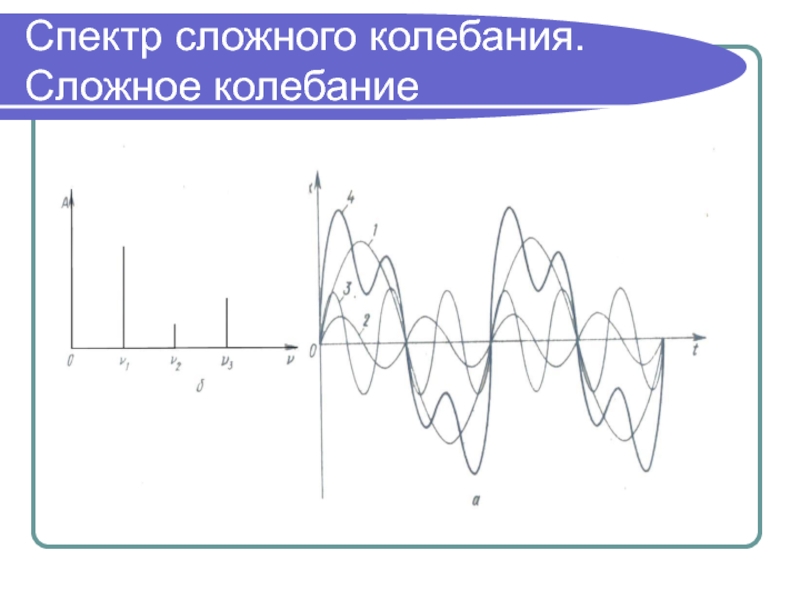
- 38. Спектр сложного колебания. Сложное колебание
- 39. БЛАГОДАРЮ ЗА ВНИМАНИЕ
- 40. Скачать презентанцию
План лекции Квазиупругие силыНезатухающие гармонические колебанияЗатухающие гармонические колебанияВынужденные колебанияРезонансАвтоколебанияЭнергия гармонических колебанияСложение гармонических колебаний
Слайды и текст этой презентации
Слайд 3Определение:
Колебания, которые совершаются по закону синуса или косинуса называются гармоническими.
Слайд 4Свободные или собственные колебания
Колебания, совершаемые под действием собственных сил без
внешнего воздействия, только при наличии начального смещения называются свободными или
собственнымиСлайд 6Квазиупругая сила
Силы, неупругие по природе, но аналогичные по свойствам силам,
возникающим при малых деформациях упругих тел, называют квазиупругими.
Слайд 11Дифференциальное уравнение затухающих колебаний
β – коэффициент затухания; ω0 – круговая
частота собственных колебаний системы.
Слайд 15Логарифмический декремент затухания
Величина, численно равная натуральному логарифму отношения двух
последовательных амплитуд колебаний, разделенных интервалом времени, равным периоду колебаний:
Слайд 16Вынужденные колебания
Вынужденными колебаниями называются такие колебания, которые возникают в
системе при участии внешней силы, изменяющейся по периодическому закону
F0
– амплитуда; ω – круговая частота колебаний вынуждающей силы Слайд 19Резонанс
Амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте
вынуждающей силы, называемой резонансной
β1 >β2 > β3
Слайд 20Автоколебания
Источник энергии
Регулятор
Колебательная система
Обратная связь
Незатухающие колебания, существующие в какой-либо системе
при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы
– автоколебательнымиСлайд 35Фигуры Лиссажу
В зависимости от отношения частот
и разности
начальных фаз
слагаемых колебаний
Слайд 37Сложение колебаний. Гармонический спектр сложного колебания
Фурье показал, что периодическая
функция любой сложности может быть представлена в виде суммы гармонических
функций, частоты которых кратны частоте сложной периодической функцииСовокупность гармонических колебаний, на которые разложено сложное колебание, называется гармоническим спектром сложного колебания