Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
К ачественные и количественные методы психологических и педагогических
Содержание
- 1. К ачественные и количественные методы психологических и педагогических
- 2. Дисциплина включает:Понятие о генеральной совокупности и выборкеСтандартизация
- 3. Генеральная совокупность и выборка. Основные понятия.Генеральная совокупность
- 4. Генеральная совокупность и выборка. Способы обеспечения свойств
- 5. Стандартизация психодиагностических методовСтандартизация - процедура получения шкалы,
- 6. Стандартизация психодиагностических методов
- 7. Стандартизация психодиагностических методов. Наиболее распространенные шкалы.Шкала Z-оценки (Z-показатель)Исходя из характеристик нормального распределения
- 8. Стандартизация психодиагностических методов. Наиболее распространенные шкалы.Шкала Z-оценки
- 9. Стандартизация психодиагностических методов.станайн 1 присваивается 4% самых
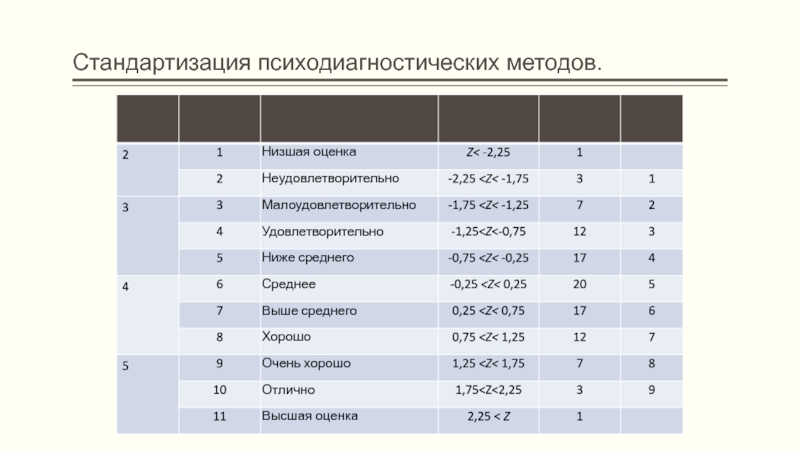
- 10. Стандартизация психодиагностических методов.
- 11. Статистические гипотезыГипотезой называется предположение, имеющее вероятностный характер,
- 12. Статистические гипотезыСтатистическая гипотеза может быть направленной или ненаправленной.
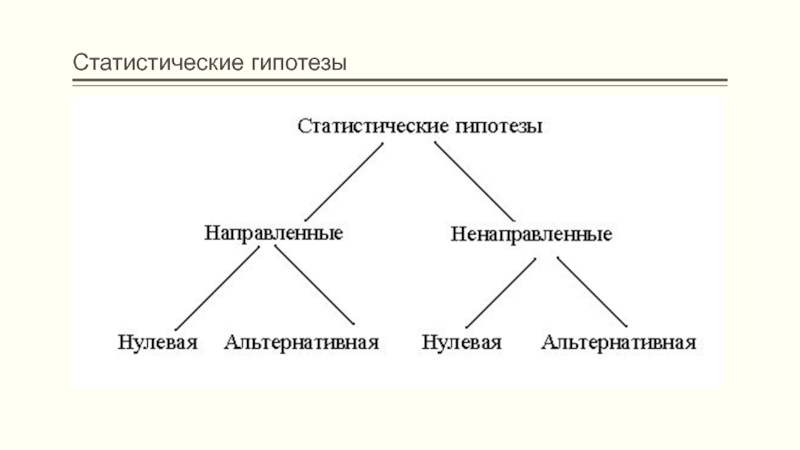
- 13. Статистические гипотезы
- 14. Статистические гипотезыСтатистический критерий - это правило, которое
- 15. Применение параметрических и непараметрических критериев:Статистические гипотезы
- 16. Понятие о психологическом шкалированииШкалирование — это процесс
- 17. Понятие о психологическом шкалированииПод формальным множеством понимается
- 18. Понятие о психологическом шкалированииМатематическая обработка данных -
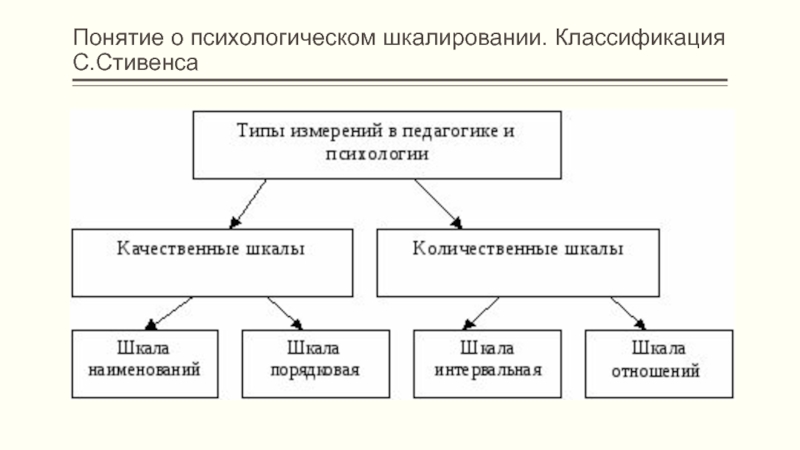
- 19. Понятие о психологическом шкалировании. Классификация С.Стивенса
- 20. Понятие о психологическом шкалировании. Классификация С.СтивенсаОтношения между
- 21. Понятие о психологическом шкалировании. Классификация С.СтивенсаШкала наименований,
- 22. Понятие о психологическом шкалировании. Классификация С.Стивенсашкала рангов
- 23. Понятие о психологическом шкалировании. Классификация С.СтивенсаШкалы интервалов
- 24. Понятие о психологическом шкалировании. Классификация С.СтивенсаШкалы отношений
- 25. Понятие о психологическом шкалировании. Классификация С.Стивенса ВАЖНО ПОМНИТЬ!!!При
- 26. Случайное событиеСлучайным событием называется событие, которое может
- 27. Случайное событиеВероятность - это то значение, к
- 28. Случайное событиеСобытия А, В, С, ... могут
- 29. Случайное событиеСуммой событий называется событие S, заключающееся
- 30. Случайная величина. Распределение случайной величины.Случайной величиной называется
- 31. Случайная величина. Распределение случайной величины.Для измерения такие
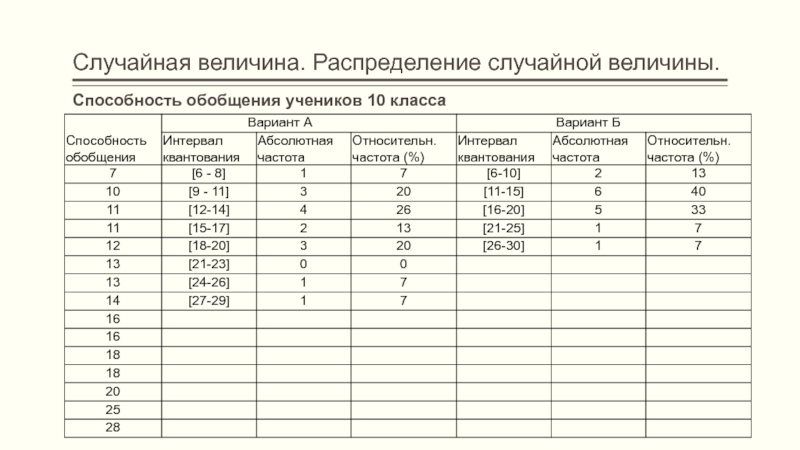
- 32. Случайная величина. Распределение случайной величины.Способность обобщения учеников 10 класса
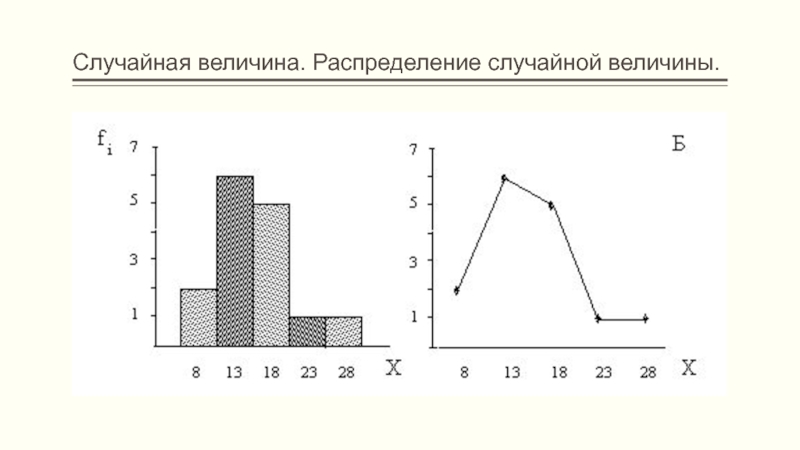
- 33. Случайная величина. Распределение случайной величины.
- 34. Случайная величина. Распределение случайной величины.
- 35. Случайная величина. Параметры распределения.Распределение случайной величины характеризуется
- 36. Случайная величина. Параметры распределения. Характеристики положения.Рассмотрим моду,
- 37. Случайная величина. Параметры распределения. Характеристики положения.Квантили -
- 38. Случайная величина. Параметры распределения. Характеристики рассеивания.Размах d
- 39. Случайная величина. Параметры распределения. Характеристики рассеивания.Коэффициент вариации
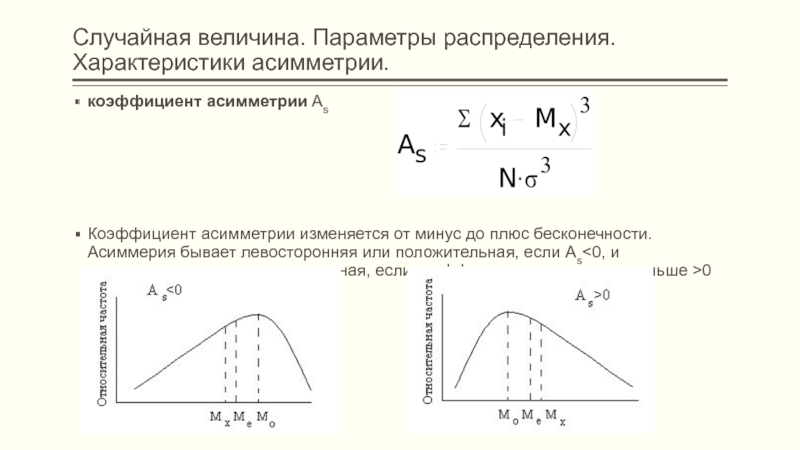
- 40. Случайная величина. Параметры распределения. Характеристики асимметрии.коэффициент асимметрии
- 41. Случайная величина. Параметры распределения. Характеристики эксцесса.Коэффициент эксцесса
- 42. Случайная величина. Нормальное распределение.
- 43. Слайд 43
- 44. Слайд 44
- 45. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Дисциплина включает:
Понятие о генеральной совокупности и выборке
Стандартизация психодиагностических методов
Статистические гипотезы
Понятие
о психологическом шкалировании
Слайд 3Генеральная совокупность и выборка. Основные понятия.
Генеральная совокупность – это множество
потенциально возможных объектов исследования
Выборка – некоторая представительная часть генеральной совокупности
Репрезентативность
– соответствие характеристик выборки характеристикам генеральной совокупностиСлайд 4Генеральная совокупность и выборка.
Способы обеспечения свойств генеральной совокупности в
выборке:
Случайная выборка
Серийная выборка
Моделирование выборки по свойствам генеральной совокупности
Слайд 5Стандартизация психодиагностических методов
Стандартизация - процедура получения шкалы, позволяющей сравнивать индивидуальный
результат по тесту с результатами большой группы испытуемых.
* Итог стандартизации
– тестовые нормы и таблицы пересчета первичных («сырых») данных в стандартные.Слайд 7Стандартизация психодиагностических методов. Наиболее распространенные шкалы.
Шкала Z-оценки (Z-показатель)
Исходя из характеристик
нормального распределения
Слайд 8Стандартизация психодиагностических методов. Наиболее распространенные шкалы.
Шкала Z-оценки (Z-показатель)
Недостаток – наличие
отрицательных и дробных показателей
Z-шкалу преобразуют (для удобства) по формуле y=az+b
a
и b - новые стандартные отклонения и среднееT-шкала Мак-Колла (а=10, b=50). T=10z + 50
Шкала Векслера. (а=15, b=100). IQ=15z + 100
Шкала Амтхауэра (а=10, b=100). IQ=10z + 100
Шкала стэнов St=2z + 5.5
Шкала станайнов
Слайд 9Стандартизация психодиагностических методов.
станайн 1 присваивается 4% самых худших результатов, станайн
9 - 4% самых лучших
станайны 2 и 8 присваивают
следующим за худшими и лучшими 7% результатов соответственностанайны 3 и 7 - следующим за ними 12% результатов
станайны 4 и 6 - следующим 17% результатов
станайн 5 присваивается 20% средним результатам группы
Слайд 11Статистические гипотезы
Гипотезой называется предположение, имеющее вероятностный характер, обладающее неопределенностью в
отношении своей истинности.
Принято выделять статистические гипотезы двух основных видов -
нулевую и альтернативную.Нулевая гипотеза, обозначаемая Н0, формулируется как гипотеза об отсутствии отличий: о сходстве двух распределений, о равенстве средних арифметических двух выборок и т.п. Нулевой она называется потому, что содержит 0: Х1-Х2=0, где Х1 и Х2 - значения признаков.
Альтернативная гипотеза Н1 противоположна по смыслу нулевой, она утверждает наличие отличий в выборках, в параметрах их распределений.
Слайд 14Статистические гипотезы
Статистический критерий - это правило, которое позволяет принимать истинную
и отклонять ложную гипотезу с высокой степенью вероятности.
Все статистические критерии
делятся наСлайд 16Понятие о психологическом шкалировании
Шкалирование — это процесс отображения по заданным
правилам эмпирических множеств в формальные
Под эмпирическим множеством понимается любая совокупность
реальных объектов (людей, животных, явлений, свойств, процессов, событий), которые находятся в определенных отношениях друг с другом и которые можно обозначить каким-либо символом. Указанные отношения могут быть представлены четырьмя типами (эмпирическими операциями):
1) равенство (равно— не равно);
2) ранговый порядок (больше — меньше);
3) равенство интервалов (больше или меньше на столько-то одинаковых интервалов как единиц измерения);
4) равенство отношений (больше или меньше во столько-то раз).
Слайд 17Понятие о психологическом шкалировании
Под формальным множеством понимается произвольная совокупность символов
(знаков, чисел, меток, слов, геометрических фигур), связанных между собой определенными
отношениями, которые соответственно эмпирическим отношениям.Они описываются четырьмя видами формальных (математических) операций:
«равно— не равно» (= #);
2) «больше — меньше» (> <);
3) «сложение — вычитание» ( + - );
4) «умножение — деление» ( х : ).
Слайд 18Понятие о психологическом шкалировании
Математическая обработка данных - это оперирование со
значениями какого-либо признака, полученными в результате психологического исследования.
Иными словами, математическая
обработка данных - это исследование результатов измерения признаков.Под измерением признака понимается приписывание объектам или событиям числовых форм в соответствии с определенными правилами.
Stanley Smith Stevens
(November 4, 1906 – January 18, 1973)
Слайд 20Понятие о психологическом шкалировании. Классификация С.Стивенса
Отношения между элементами эмпирического множества
и соответствующие допустимые математические операции (допустимые преобразования) обуславливают уровень шкалирования
и тип получаемой шкалы (по классификации С.С. Стивенса)первому, наиболее простому типу отношений (= #) соответствуют наименее информативные шкалы наименований,
второму (> <) — шкалы порядка,
третьему (+ -) — шкалы интервалов,
четвертому (х :) — самые информативные шкалы отношений.
Слайд 21Понятие о психологическом шкалировании. Классификация С.Стивенса
Шкала наименований, она же номинативная
или номинальная шкала.
наименование не измеряется количественно, оно лишь позволяет отличить
один предмет (явление) от другого. Номинативная шкала - это способ распределения объектов или явлений по классификационным ячейкам.В простейшем случае номинативная шкала состоит из двух ячеек (“да - нет”), и она называется дихотомической. Более сложный вариант номинативной шкалы - классификация из трех и более ячеек
распределив объекты или реакции испытуемых по ячейкам классификации и сосчитав количество наблюдений в каждой из ячеек, то есть частоту встречаемости того или иного признака, мы получаем возможность перейти от наименований к числам.
Психологическая основа построения — процессы идентификации и опознания.
Вывод: при использовании шкалы наименований единицей измерения является «одно наблюдение».
Допустимыми преобразованиями на шкале наименований являются любые взаимнооднозначные подстановки
Слайд 22Понятие о психологическом шкалировании. Классификация С.Стивенса
шкала рангов (или порядковая шкала)
классифицирует
объекты по принципу “больше”- “меньше”. Здесь мы группируем объекты в
три или более классов, придавая, обычно, объектам с наименее выраженными свойствами наименьшее значение ранга (класса) - 1, с несколько более выраженными свойствами - 2, и так далее по возрастающей.Все психологические методы, основанные на ранжировании, используют шкалу порядка.
В порядковой шкале (шкале рангов) единица измерения - 1 класс (ранг). Расстояние между классами нам неизвестно, оно может быть одинаковым, может быть различным.
Психологическая основа построения шкалы — процессы различения и предпочтения.
Вывод: допустимыми на шкале порядка являются любые преобразования, соответствующие монотонно возрастающим или убывающим функциям.
Слайд 23Понятие о психологическом шкалировании. Классификация С.Стивенса
Шкалы интервалов (разностей, расстояний, равных
интервалов)
дают метрическое выражение измеряемых величин, поскольку расстояние между точками
на континууме может быть точно задано, то есть может быть определена величина интервала. Шкала указывает «на сколько» один объект отличается от другого.
Допустимые преобразования для шкал интервалов ограничены линейной группой - y=ax+b
Вывод: произвольность выбора начальной точки отсчета, следовательно, отсутствие естественного начала отсчета (абсолютного нуля) является характерной особенностью шкал интервалов.
Психологическая основа шкалы — способность к уравниванию сенсорных расстояний.
Слайд 24Понятие о психологическом шкалировании. Классификация С.Стивенса
Шкалы отношений (равных отношений, пропорциональные
шкалы).
Классифицирует объекты или субъекты пропорционально степени выраженности измеряемого свойства,
то есть предполагает равенство отношения степени выраженности какого-либо психологического свойства двух объектов отношению двух чисел, приписываемых этим объектам для характеристики свойства.Шкала отношений предполагает наличие всех свойств шкал предыдущих уровней и сверх того — наличие естественной точки отсчета, то есть абсолютного (истинного) нуля, что дает дополнительную информацию о соотношении выраженности исследуемых признаков - принципиальная разница между шкалами интервалов и отношений
По шкале отношений мы можем представить, во сколько раз свойство одного испытуемого превосходит свойство другого.
Вывод: шкала отношений используется, в основном, при психофизиологических исследованиях явлений, измеряемых в физических единицах (метры, граммы, секунды и т.д.). Для большинства психологических явлений шкала отношений не применяется (абсолютная глупость)
Психологическая основа шкал отношений — способность человека к установлению отношений между ощущениями.
Слайд 25Понятие о психологическом шкалировании. Классификация С.Стивенса
ВАЖНО ПОМНИТЬ!!!
При математической обработке данных
в случае необходимости всегда можно перейти к шкале более низкого
порядка - от шкалы интервалов, например, к шкале рангов или наименований.В то же время переход к шкале более высокого порядка (от шкалы наименований, к примеру, к шкале рангов) невозможен без дополнительных исследований.
Слайд 26Случайное событие
Случайным событием называется событие, которое может произойти либо не
произойти, либо произойти в той или иной степени.
Численными мерами
появления случайного события являются абсолютная частота, относительная частота и вероятность.Абсолютная частота - это просто количество событий, интересующих исследователя. Абсолютную частоту принято обозначать символом
Относительная частота - это абсолютная частота, отнесенная к общему количеству событий в некотором опыте.
Слайд 27Случайное событие
Вероятность - это то значение, к которому стремится относительная
частота при бесконечном увеличении числа опытов.
Выражается она в виде
положительного числа, большего нуля и меньшего 1 (либо от 0 до 100%), и является понятием идеальным, поскольку на практике количество опытов всегда ограничено. Вероятность равна 0, если событие абсолютно невероятно, и равна 1 (или 100%) если событие неизбежно.
Вероятность принято обозначать буквой “р”
Слайд 28Случайное событие
События А, В, С, ... могут быть совместными и
несовместными, зависимыми и независимыми.
Совместными называются события, которые могут произойти
одновременно в одном и том же опытеНесовместными будут события, которые одновременно произойти не могут
Полной группой событий называется множество несовместных событий, одно из которых произойдет обязательно
Зависимыми называются события, появление одного из которых оказывает влияние на вероятность другого.
Если такое влияние отсутствует, то события являются независимыми.
Слайд 29Случайное событие
Суммой событий называется событие S, заключающееся в том, что
произойдет или одно, или другое, или третье и т.д. событие,
т.е. S=А+В+С+... .Произведением событий называется событие W, заключающееся в том, что произойдет и первое, и второе, и третье и т.д. событие: W=AхBхC... .
Для сумм и произведений событий выполняются следующие правила:
1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий Р(A+B+C+...)= P(A)+P(B)+P(С)+...P(Z).
2. Вероятность произведения независимых событий равна произведению вероятностей этих событий Р(AхBхCх... хZ) = P(A)хP(B)хP(С) ... хP(Z).
Слайд 30Случайная величина. Распределение случайной величины.
Случайной величиной называется такая переменная величина,
которая принимает значения из некоторого множества.
Принято выделять дискретные и
непрерывные случайные величины. Дискретная случайная величина принимает свои значения из множества целых чисел
Непрерывная случайная величина принимает свои значения из множества действительных чисел.
Ряд психологических явлений непрерывен по своей природе.
Слайд 31Случайная величина. Распределение случайной величины.
Для измерения такие явления разбиваются в
числовой оси на равные интервалы.
Операция разбиения числовой оси на равные
интервалы называется квантованием, а полученные интервалы - интервалами квантования.Основной способ описания случайной величины - построение ее распределения.
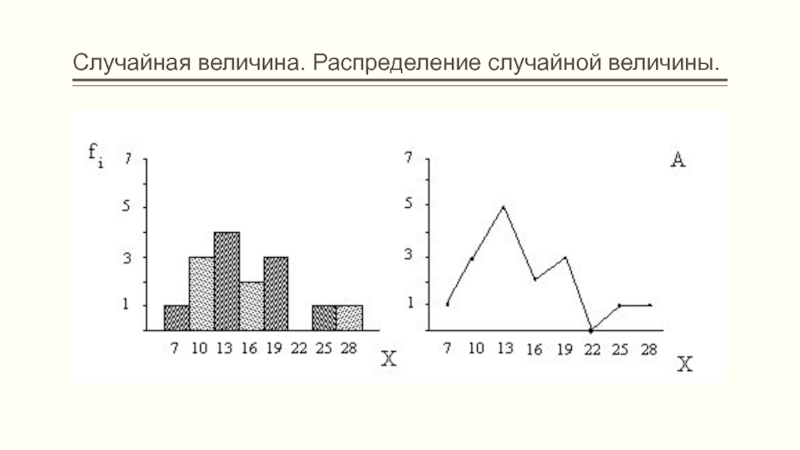
Слайд 32Случайная величина. Распределение случайной величины.
Способность обобщения учеников 10 класса
Слайд 35Случайная величина. Параметры распределения.
Распределение случайной величины характеризуется параметрами распределения, которые
объединены в четыре группы характеристик:
характеристики положения,
характеристики рассеивания,
характеристики асимметрии,
характеристики эксцесса.
!!! Параметры
распределения определяются только для данных, представленных либо в интервальной шкале, либо в шкале отношений.Слайд 36Случайная величина. Параметры распределения.
Характеристики положения.
Рассмотрим моду, медиану и среднее арифметическое
значение.
По-другому эти параметры называются мерами центральной тенденции.
Мода (М0) -
наиболее часто встречающееся значение; его называют также модальным значением.Распределение величины может быть унимодальным и полимодальным
Среднее арифметическое значение Мх
Медиана (Ме) - это такое значение случайной величины, которое делит упорядоченную (в порядке возрастания или убывания величины) выборку пополам, то есть справа и слева от медианы находится равное количество значений случайной величины.
Слайд 37Случайная величина. Параметры распределения.
Характеристики положения.
Квантили - это такие значения случайной
величины, которые делят распределение на равные части. Есть несколько разновидностей
квантилей:Квартили делят распределение на 4 равных части по 25%, соответственно квартилей три Q1, Q2, Q3.
Квинтили - их 4 (К1 ....К4), они делят распределение на 5 частей по 20% в каждой.
Децили. Девять децилей (D1 ... D9) делят распределение на 10 частей по 10%.
Процентили в количестве 99 (Р1....Р99) делят распределение на 100 частей по 1%.
Процентили нельзя путать с процентными показателями.
Процентные показатели - это первичные показатели, определяющие количество правильно выполненных заданий.
Процентиль - показатель производный, указывающий на долю от общего числа членов группы
Слайд 38Случайная величина. Параметры распределения.
Характеристики рассеивания.
Размах d - это разность между
максимальным и минимальным значениями случайной величины: d = хmax –
хminДисперсия 2 (или D) характеризует разброс значений случайной величины вокруг среднего арифметического значения
Среднеквадратическое или стандартное отклонение
Слайд 39Случайная величина. Параметры распределения.
Характеристики рассеивания.
Коэффициент вариации размерности не имеет, он
служит для сравнения вариативности, то есть изменчивости случайных величин, имеющих
различную природу.Если коэффициент вариации меньше 40%, то он признается низким, то есть изменчивость величины невелика.