Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геодезия " ge" - земля и "dazomai" - разделяю, делю на части "землеразделение"
Содержание
- 1. Геодезия " ge" - земля и "dazomai" - разделяю, делю на части "землеразделение"
- 2. Топография (от греч. tópos – место и
- 3. ЭРАТОСФЕН Киренский (ок. 276–194 до н. э.), Определил длину окружности
- 4. Понятие о фигуре Земли. Уровенная поверхность. Отвесная
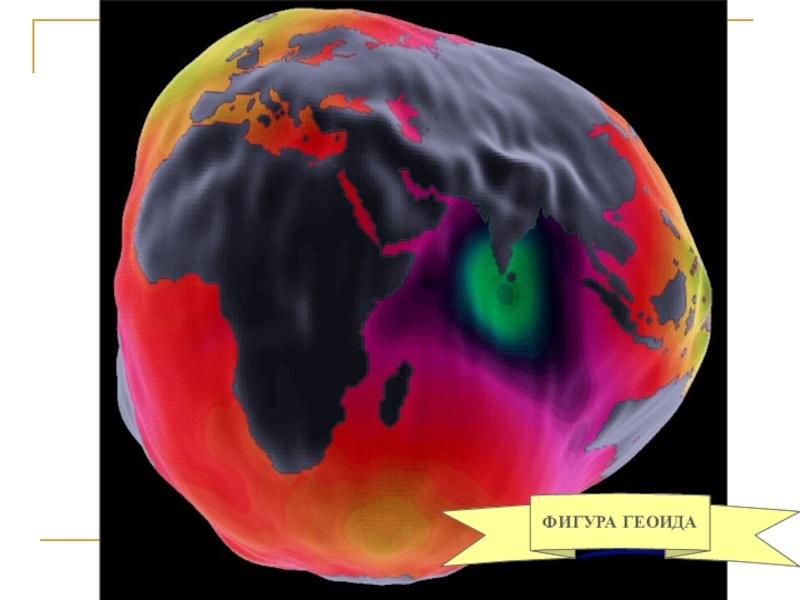
- 5. ФИГУРА ГЕОИДА
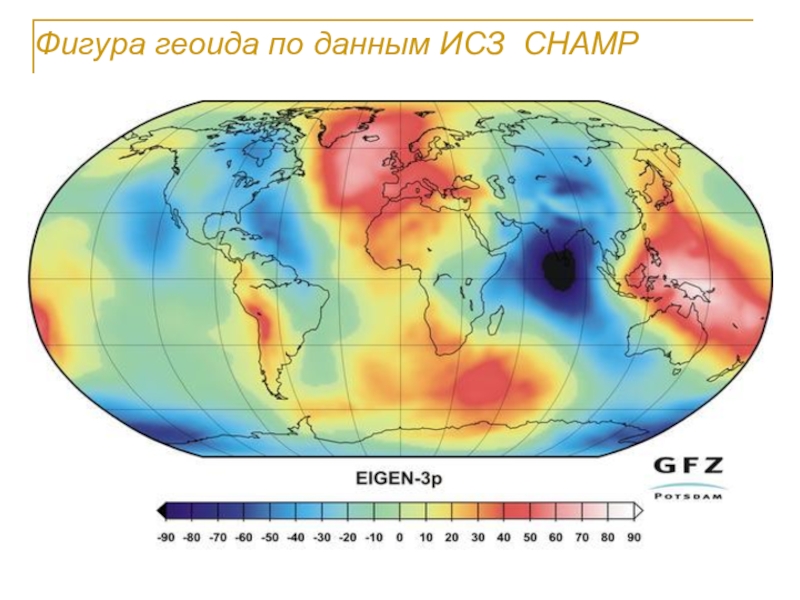
- 6. Фигура геоида по данным ИСЗ CHAMP
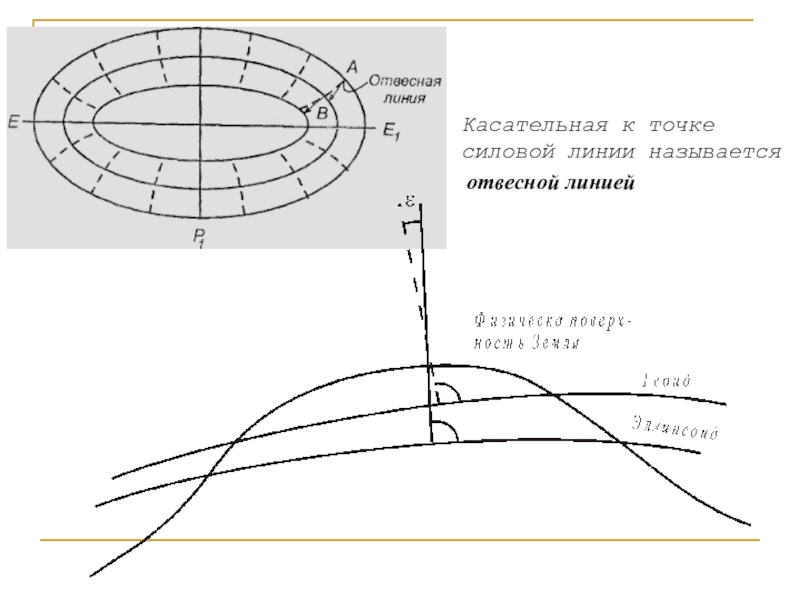
- 7. Касательная к точкесиловой линии называется отвесной линией
- 8. Поверхность относимостиПоверхность относимости – правильная математическая поверхность,
- 9. Поверхность относимостиЗемной эллипсоид (общий земной эллипсоид, сфероид)
- 10. Поверхность относимостиВ России принят общий земной эллипсоид
- 11. ЭллипсоидNbaSf = a-b = сжатие
- 12. Эллипсоид ЭллипсоидWGS 84ГеоидЭллипсоидКрасовского
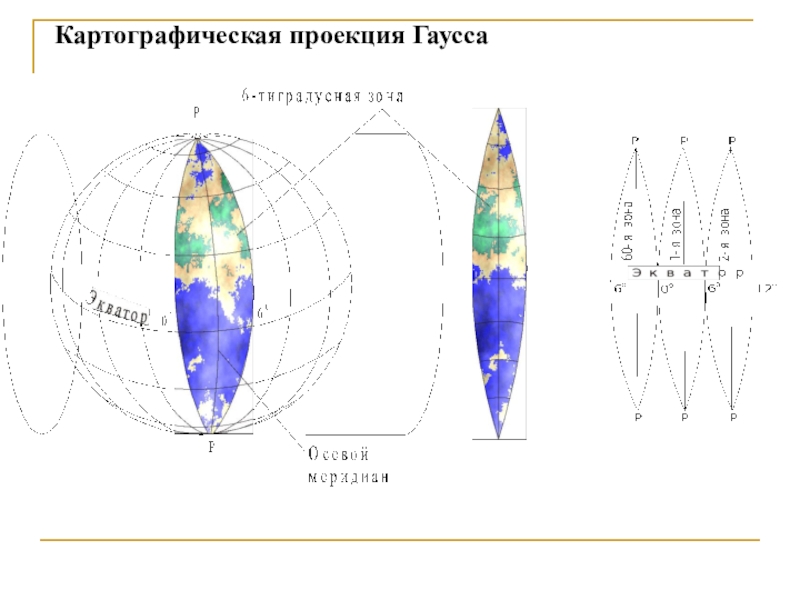
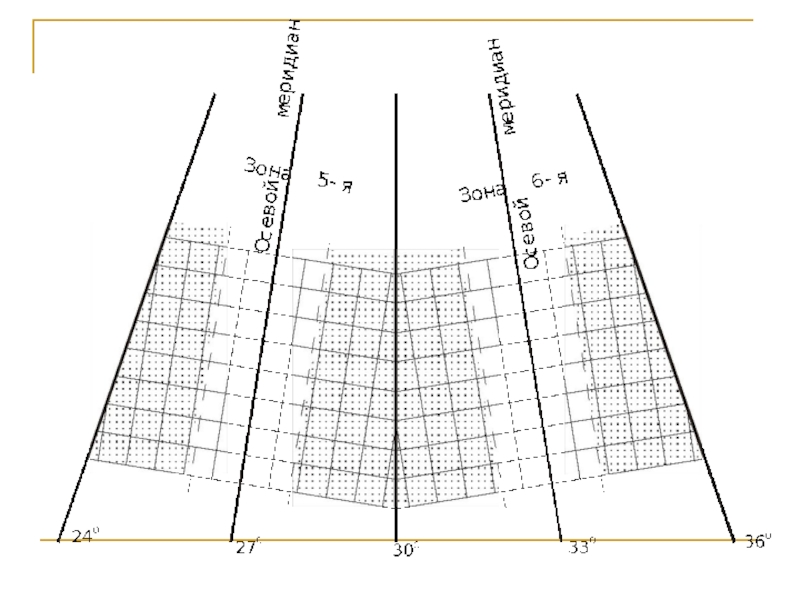
- 13. Картографическая проекция Гаусса
- 14. Слайд 14
- 15. Слайд 15
- 16. Основные системы координат, используемые в геодезии Система
- 17. Астрономической широтой φ называют угол между
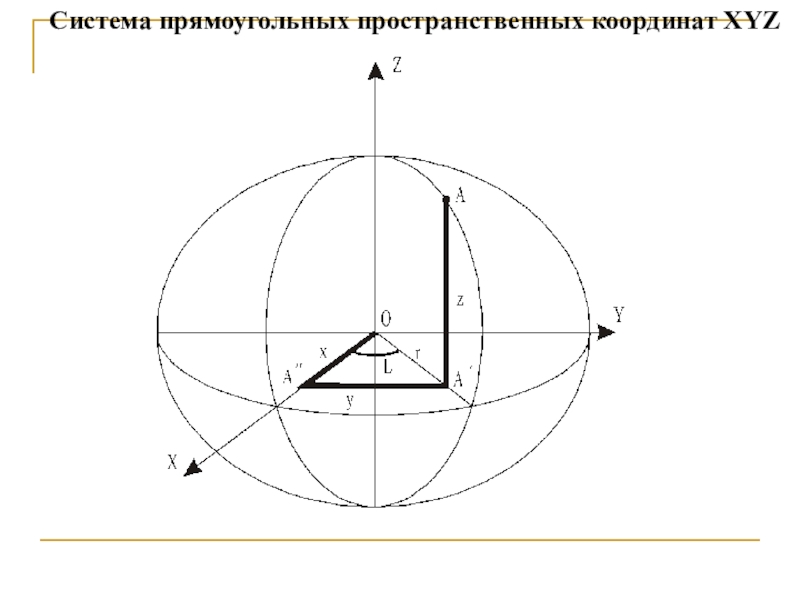
- 18. Система прямоугольных пространственных координат XYZ
- 19. Плоские прямоугольные координаты
- 20. Полярные координаты
- 21. Связь плоской прямоугольной и полярной систем
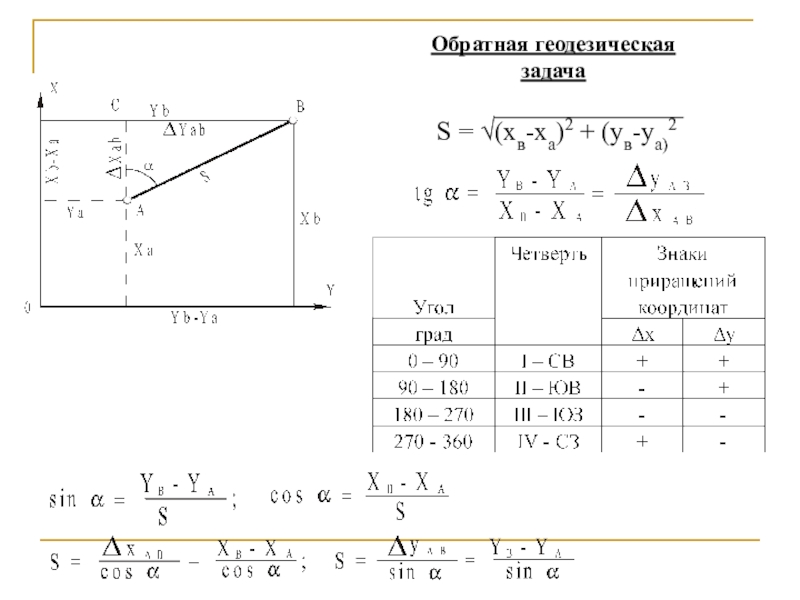
- 22. Обратная геодезическая задача S = √(хв-ха)2 + (ув-уа)2
- 23. План и картаПлан – это уменьшенное, подобное
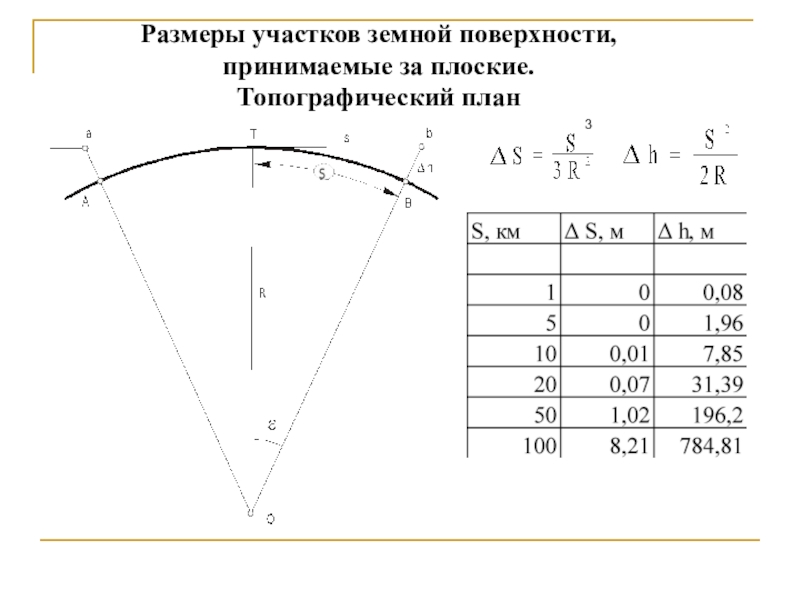
- 24. Размеры участков земной поверхности,принимаемые за плоские.Топографический план 3
- 25. Основные свойства картографического изображения земной поверхности –
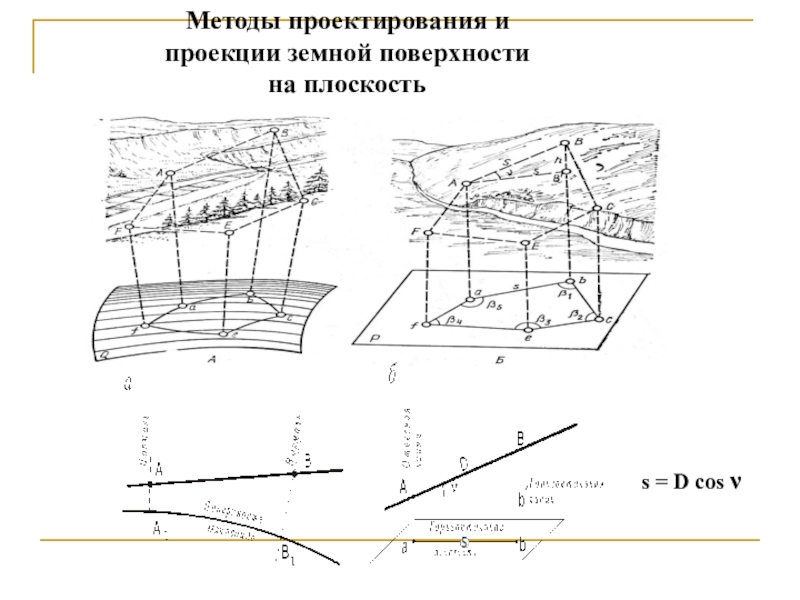
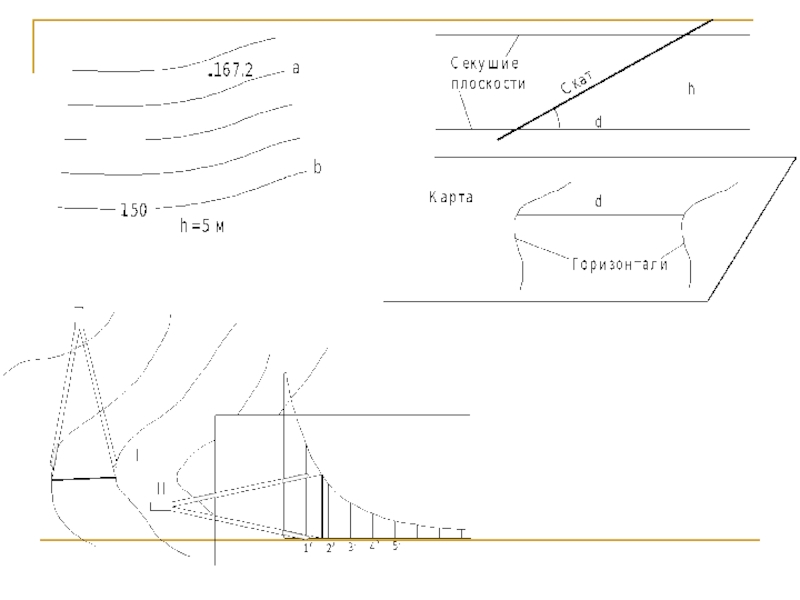
- 26. Методы проектирования и проекции земной поверхности на плоскость s = D cos ν
- 27. Картографические условные знаки – это применяемыена картах
- 28. Слайд 28
- 29. Ориентирование линийОриентировать линию - найти ее направление
- 30. Исходные направленияВ геодезии в качестве исходного принимают направления:- истинного меридиана;- магнитного меридиана;- осевого меридиана зоны.MN
- 31. Истинный азимутВ качестве исходного направления принято направление
- 32. Магнитный азимутВ качестве исходного направления принято направление
- 33. Дирекционный уголВ качестве исходного направления принято направление
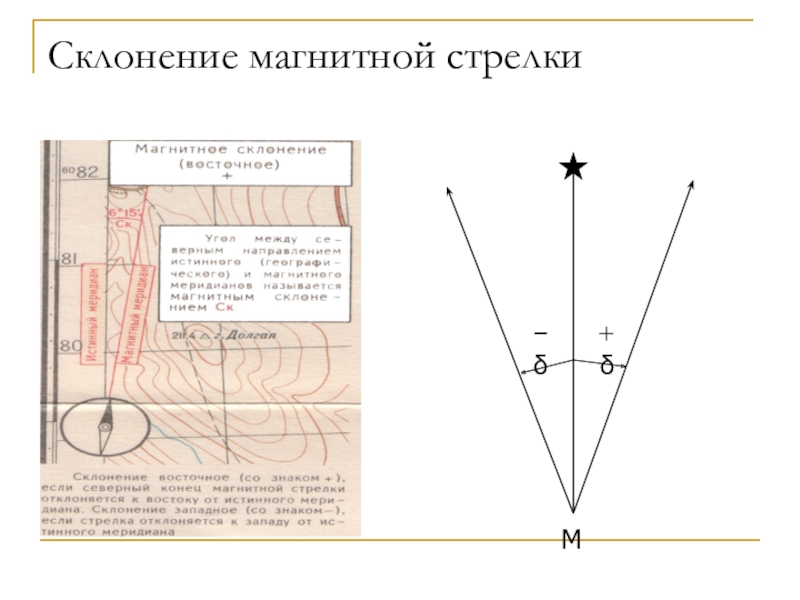
- 34. Склонение магнитной стрелкиM+ -
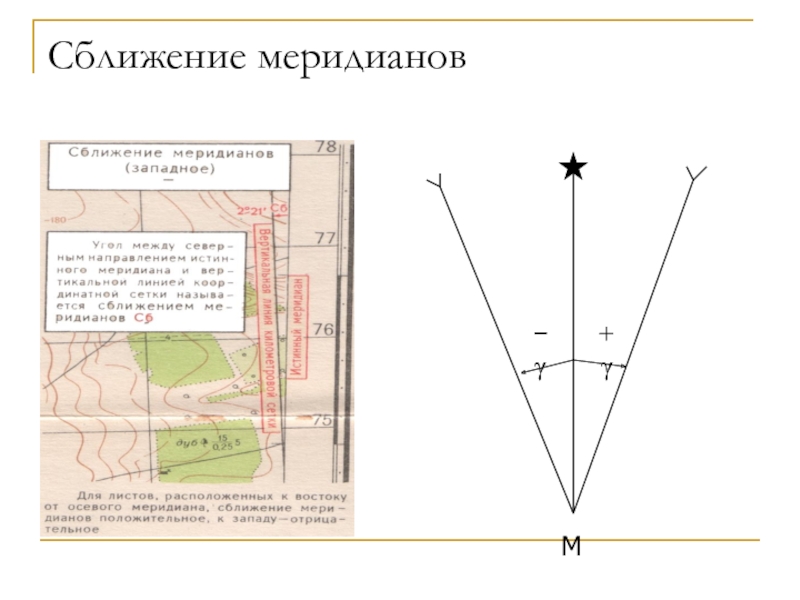
- 35. Сближение меридиановM+-
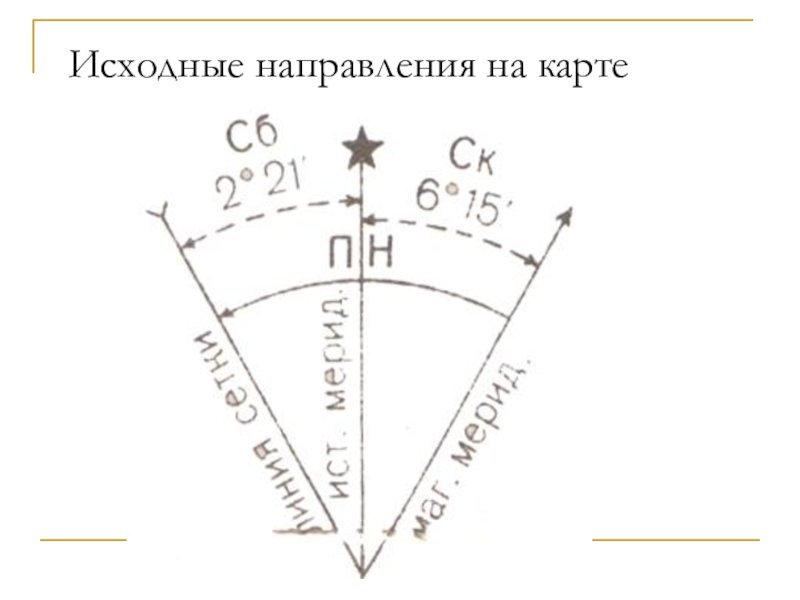
- 36. Исходные направления на карте
- 37. Сближение меридианов и его определение γ = (L – L0) sin B
- 38. Румбы и табличные углыРумбом называется острый угол,
- 39. Балтийская система высотВысота точки А – это
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. HH = ортометрическая высота
- 44. Уровенные поверхности и ортометрические высотыУровенные поверхностиОтвеснаялиния“Геоид”POPУровенная поверхность
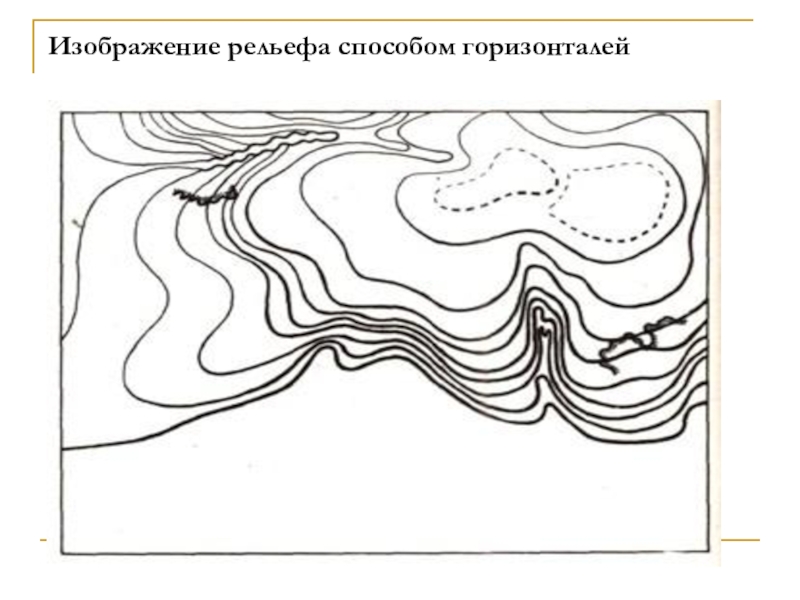
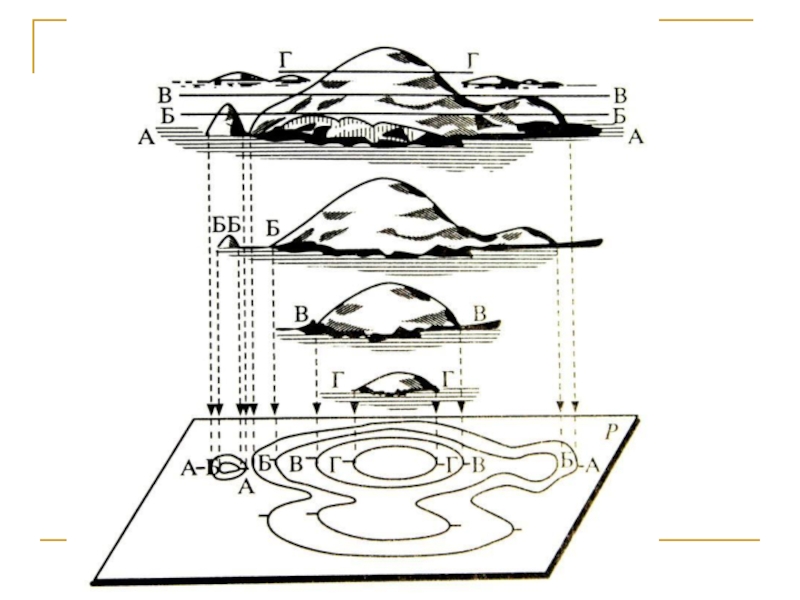
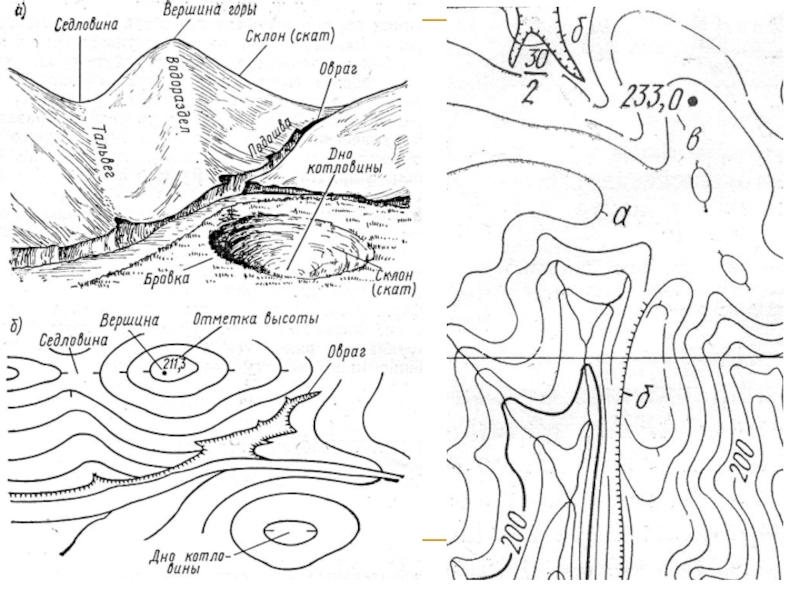
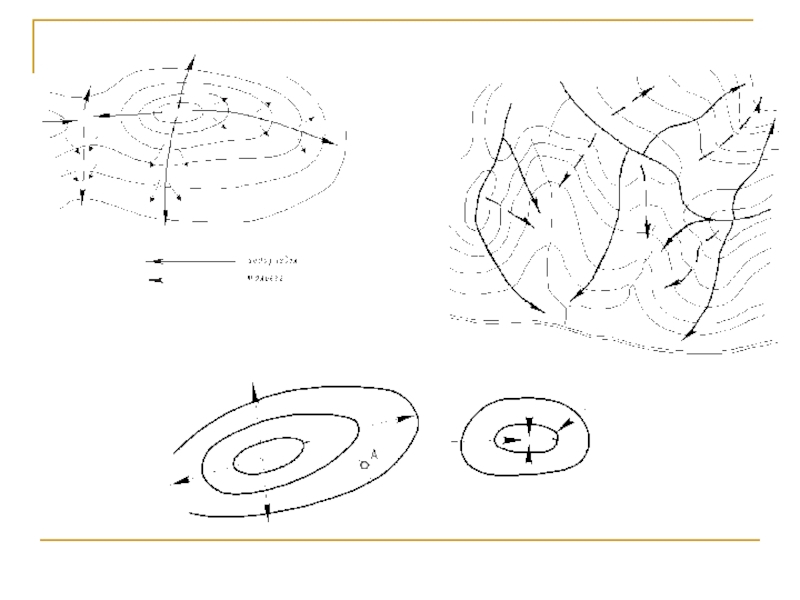
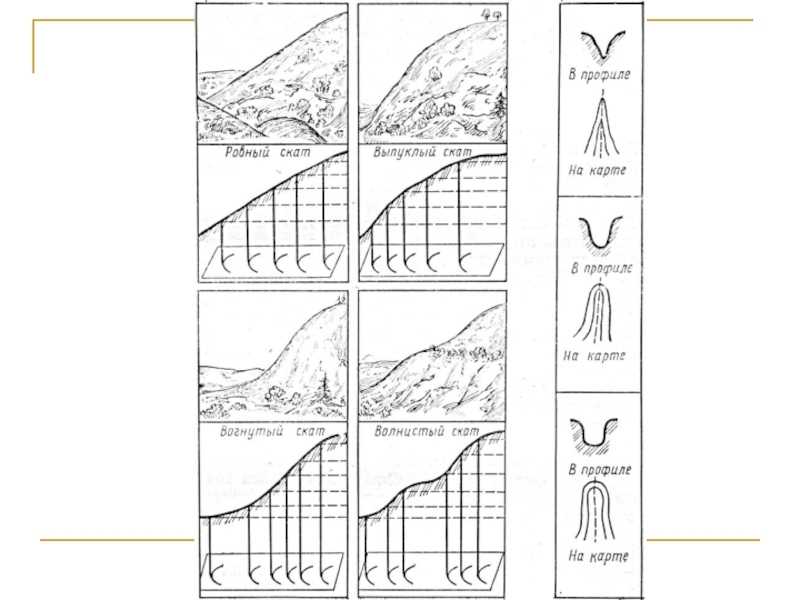
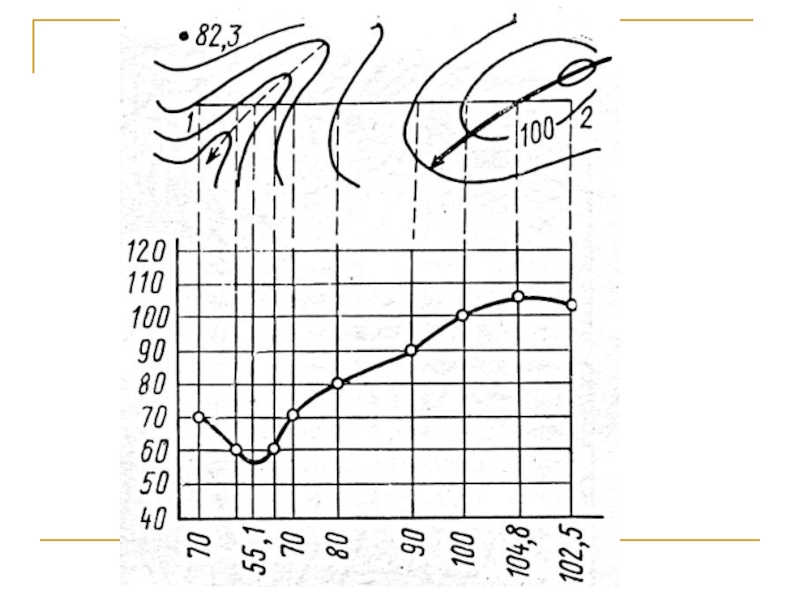
- 45. Изображение рельефа способом горизонталей
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Съемка территории. Составление плана участка местностиПланово-высотное обоснование
- 53. Съемка территории. Составление плана участка местностиСхема теодолитного хода2прим345Dср(1-2)Dср(2-3)Dср(3-4)Dср(4-5)Dср(5-1)Направление хода1Аxy1xy2345Направление на СеверXYαA-1X
- 54. 9 КЖ154,710,08,04,24,714,911,9Съемка территории. Составление плана участка местностиСпособы
- 55. Съемка территории. Составление плана участка местностиСпособы съемки
- 56. Съемка территории. Составление плана участка местностиКамеральные работыРешение
- 57. Съемка территории. Составление плана участка местностиВычисления в ведомости координат. Вычисление дирекционных угловС Северαпредαпослβправαпред180°С СеверАВDβлев
- 58. Съемка территории. Составление плана участка местностиВычисления в
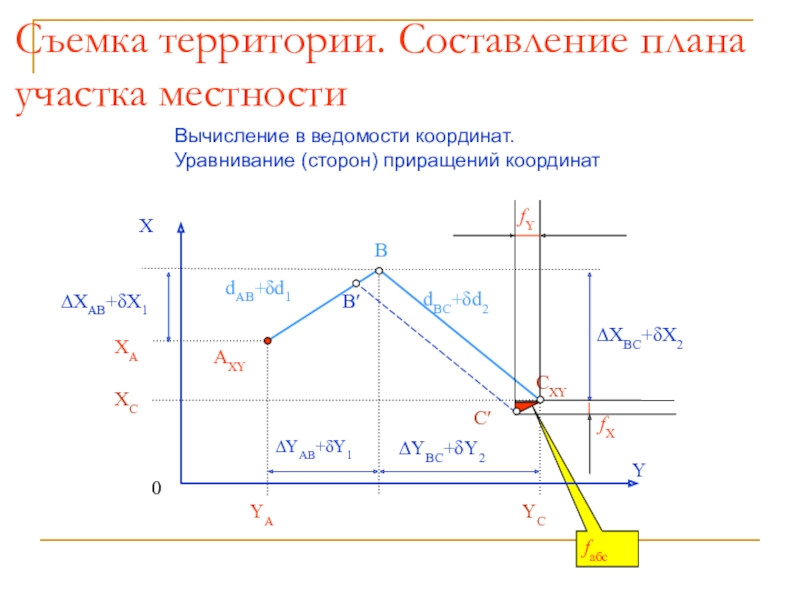
- 59. Съемка территории. Составление плана участка местностиВычисление в ведомости координат. Уравнивание (сторон) приращений координат
- 60. Съемка территории. Составление плана участка местностиВычисление в
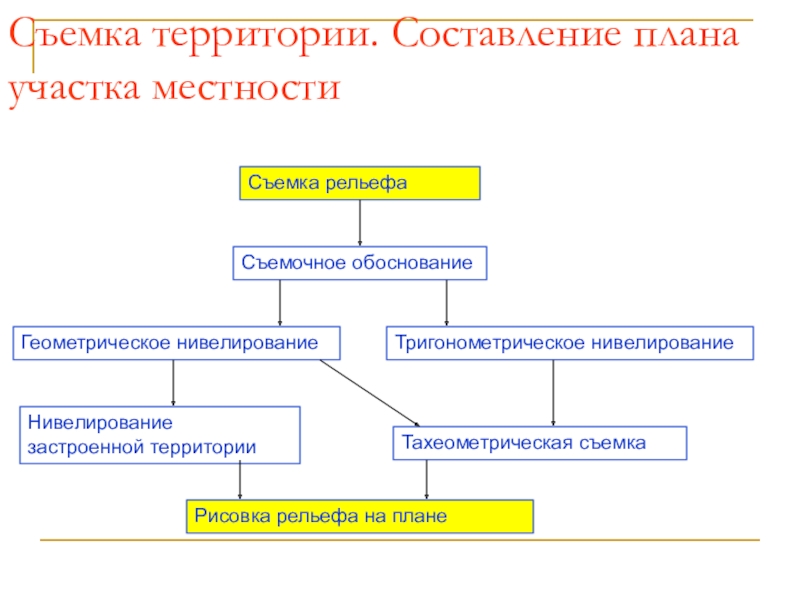
- 61. Съемка территории. Составление плана участка местностиСъемка рельефаСъемочное обоснованиеГеометрическое нивелированиеТригонометрическое нивелированиеНивелирование застроенной территорииТахеометрическая съемкаРисовка рельефа на плане
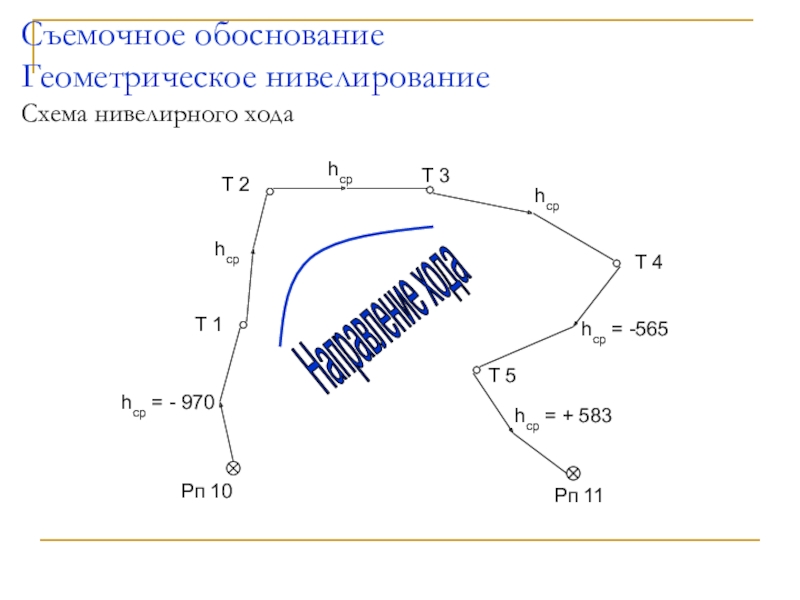
- 62. Съемочное обоснование Геометрическое нивелирование Схема нивелирного ходаТ
- 63. Съемочное обоснование Геометрическое нивелирование Уравнивание превышенийИсходные данные:Средние
- 64. Тахеометрическая съемкаПолевые работы:Разбивка и закрепление съемочного обоснованияИзмерение
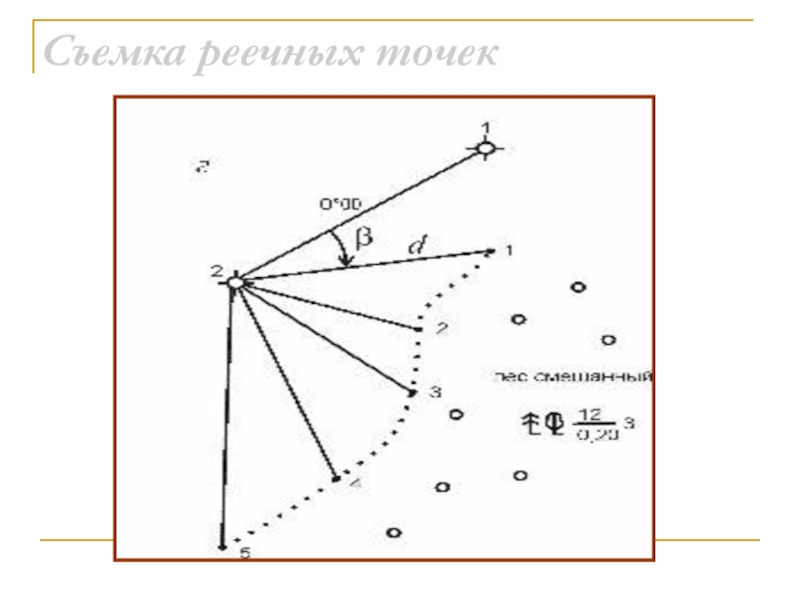
- 65. Съемка реечных точек
- 66. Порядок работ на станции:Устанавливают теодолит над вершиной
- 67. Виды нивелирования - геометрическое нивелирование – это метод
- 68. Нивелирование вперед h = i – b, т.е. превышение равно высоте нивелира минус отсчет по рейке.
- 69. Геометрическое нивелирование из середины h = a
- 70. Зная высоту НА точки А и превышение
- 71. Высоту точки В можно также получить при
- 72. ГП = НА + а, т.е. высоте
- 73. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Геодезия "ge" - земля и "dazomai" - разделяю, делю на
части "землеразделение".
и размеров Земли, методах изображения ее поверхности на картах и планах, а также о способах проведения различных измерений на поверхности Земли (на суше и акваториях), под землей, в околоземном пространстве и на других планетах.Слайд 2Топография
(от греч. tópos – место и греч. gráphō –
пишу, описание местности)
Картография
Высшая геодезия
Фотограмметрия
Инженерная геодезия
Маркшейдерия
Спутниковая геодезия
Космическая геодезия
Слайд 3ЭРАТОСФЕН Киренский
(ок. 276–194 до н. э.),
Определил длину окружности земного шара в
250 тысяч стадиев (39 250 километров)
S/2R = /360º
S=0,5(158+185)5000=857500 м,
Δφ =7°12‘ =
7.2 °,имеем R=6823,8 км
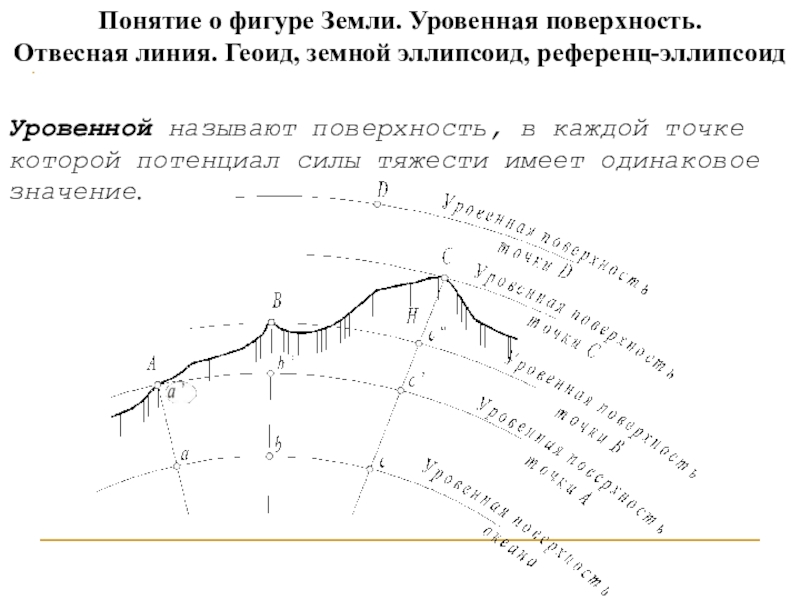
Слайд 4Понятие о фигуре Земли. Уровенная поверхность.
Отвесная линия. Геоид, земной
эллипсоид, референц-эллипсоид
Уровенной называют поверхность, в каждой точке которой потенциал силы
тяжести имеет одинаковое значение.Слайд 8Поверхность относимости
Поверхность относимости – правильная математическая поверхность, на которую проектируют
геодезические измерения (плоскость, шар, эллипсоид).
Метод проектирования – это способ переноса
измеренных на физической поверхности Земли величин на поверхность относимости. В геодезии применяют проектирование по линиям, перпендикулярным к поверхности относимости.Слайд 9Поверхность относимости
Земной эллипсоид (общий земной эллипсоид, сфероид) – математически правильная
поверхность, образованная вращением эллипса вокруг малой оси, близкая к поверхности
геоида в целом.Референц-эллипсоид – эллипсоид, ориентированный в теле Земли для близости к геоиду на определенной территории. Его центр может не совпадать с центром масс Земли, а ось вращения не совпадать с осью вращения Земли, но быть параллельна ей.
Слайд 10Поверхность относимости
В России принят общий земной эллипсоид ПЗ-90
(а = 6378136 м, f = 1/298,257839303), на нем
задаются координаты для глобальной навигационной системы ГЛОНАСС, и референц-эллипсоид Красовского (а = 6378245 м, b = 6356863 м, f =1/298,3), на котором определяются государственные референцные системы координат СК-42 и СК-95.Для американской глобальной навигационной системы GPS используется эллипсоид WGS-84 (а = 6378137 м, f = 1/298,2572235бЗ).

Слайд 11Эллипсоид
N
b
a
S
f = a-b = сжатие
a
a =
6378245 м
1/f = 298.3
Эллипсоид Красовского
a = большая полуось
b = малая
полуосьb = 6356863 м
Слайд 16Основные системы координат, используемые в геодезии
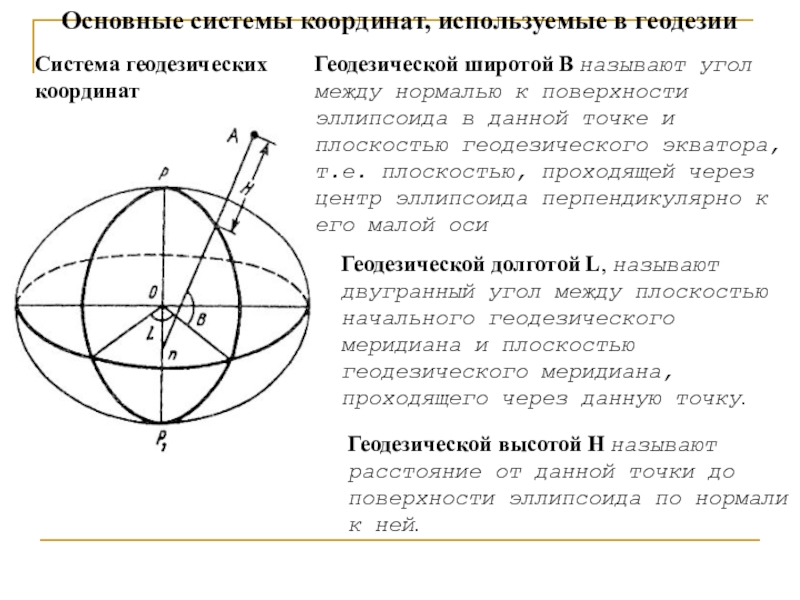
Система геодезических координат
Геодезической
широтой В называют угол между нормалью к поверхности эллипсоида в
данной точке и плоскостью геодезического экватора, т.е. плоскостью, проходящей через центр эллипсоида перпендикулярно к его малой осиГеодезической долготой L, называют двугранный угол между плоскостью начального геодезического меридиана и плоскостью геодезического меридиана, проходящего через данную точку.
Геодезической высотой Н называют расстояние от данной точки до поверхности эллипсоида по нормали к ней.
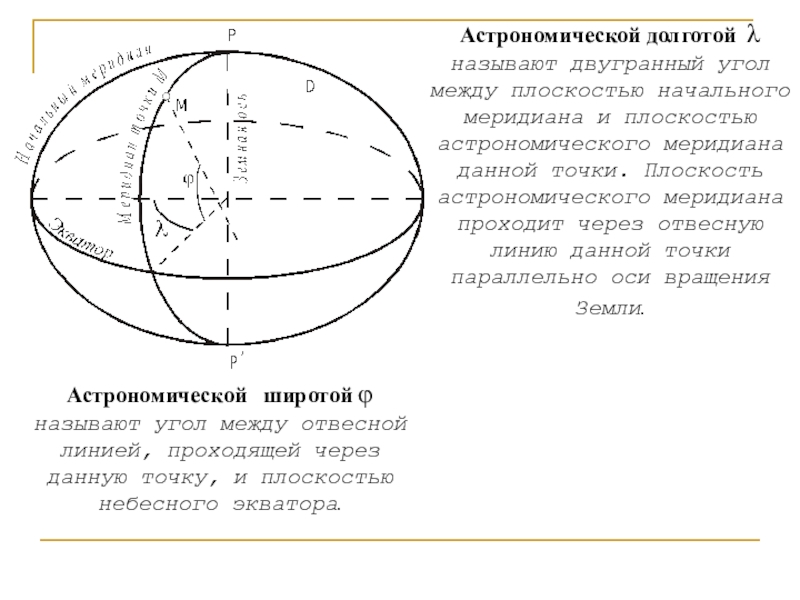
Слайд 17Астрономической широтой φ называют угол между отвесной линией, проходящей
через данную точку, и плоскостью небесного экватора.
Астрономической долготой λ
называют двугранный угол между плоскостью начального меридиана и плоскостью астрономического меридиана данной точки. Плоскость астрономического меридиана проходит через отвесную линию данной точки параллельно оси вращения Земли. Слайд 21 Связь плоской прямоугольной и полярной систем координат
XB =
XA + ΔXAB
YB = YA + ΔYAB
XAB = S
cos α, YAB = S sin αXB = XA + S cos α, YB = YA + S sin α
Прямая геодезическая задача состоит в определении координат конечной точки линии по длине ее горизонтального проложения, направлению и координатам начальной точки
Слайд 23План и карта
План – это уменьшенное, подобное изображение на горизонтальной
плоскости небольшого плоского участка местности
(признаки плана: уменьшенное, подобное, плоское)
Карта
– это уменьшенное, обобщенное изображение на горизонтальной плоскости сферической поверхности Земли, выполненное в определенной картографической проекции (признаки карты: уменьшенное, обобщенное, с учетом сферичности Земли)
Масштаб – это степень уменьшения изображения участка местности на плане или карте (1: 10000, в 1 см – 100 м)
Слайд 25Основные свойства картографического изображения земной поверхности – наглядность и измеримость
Наглядность и измеримость карты обусловливаются:
наличием математически определенной связи между
многомерными объектами окружающего нас мира и их плоским картографическим изображением; она осуществляется с помощью картографических проекций; 2) известной степенью уменьшения линейных размеров изображенных объектов, которая зависит от масштаба;
выделением типических черт местности, определяющих ее отличительные особенности, путем картографической генерализации;
4) применением для изображения земной поверхности особой знаковой системы - картографических условных знаков
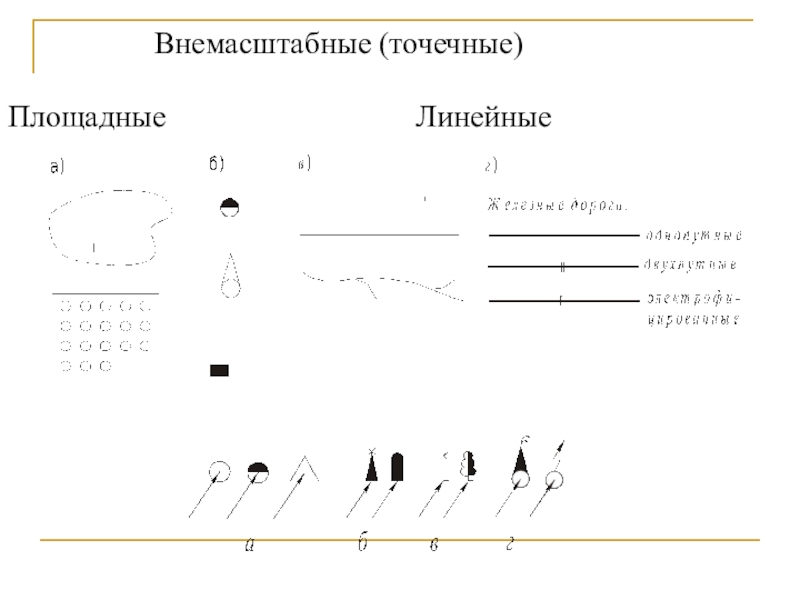
Слайд 27Картографические условные знаки – это применяемые
на картах обозначения различных объектов
и их качественных
и количественных характеристик.
Условные знаки – это система графических,
цветовых
и буквенно-цифровых обозначений.Слайд 29Ориентирование линий
Ориентировать линию - найти ее направление относительно какого-либо другого
направления, принимаемого за исходное (известное) направление.
Для этого необходимо определить значение
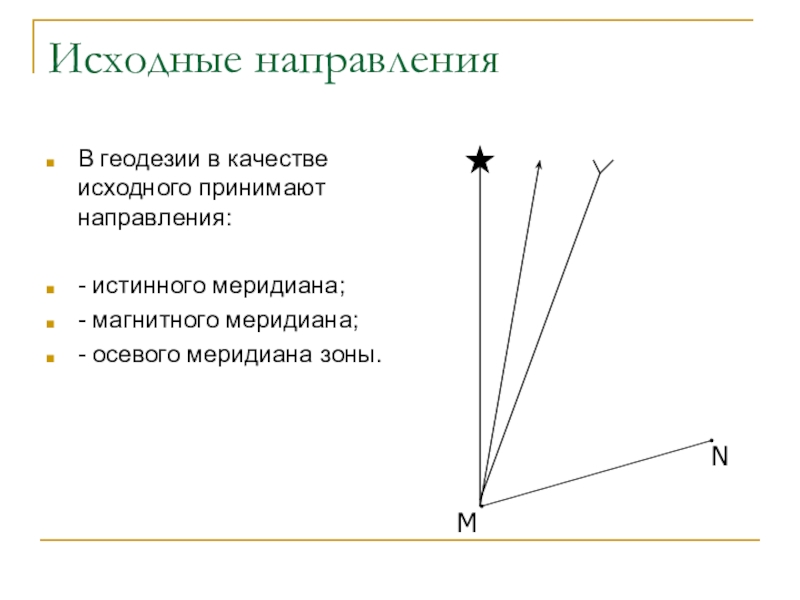
горизонтального угла между исходным и определяемым направлениями.Слайд 30Исходные направления
В геодезии в качестве исходного принимают направления:
- истинного меридиана;
-
магнитного меридиана;
- осевого меридиана зоны.
M
N
Слайд 31Истинный азимут
В качестве исходного направления принято направление истинного меридиана.
Истинный азимут
Аи - горизонтальный угол, измеряемый по ходу часовой стрелки между
северным направлением истинного (географического) меридиана и заданным направлением.0 Аи 360
M
N
Аи
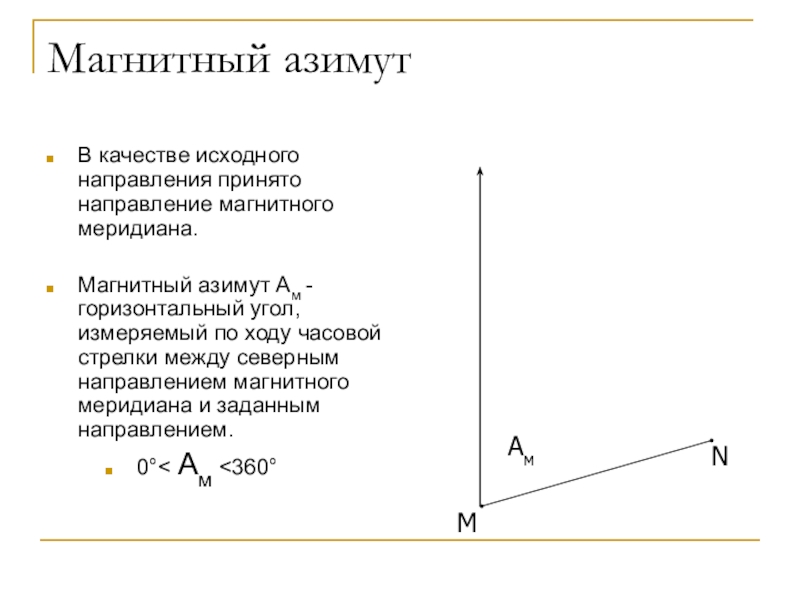
Слайд 32Магнитный азимут
В качестве исходного направления принято направление магнитного меридиана.
Магнитный азимут
Ам - горизонтальный угол, измеряемый по ходу часовой стрелки между
северным направлением магнитного меридиана и заданным направлением.0 Ам 360
M
N
Ам
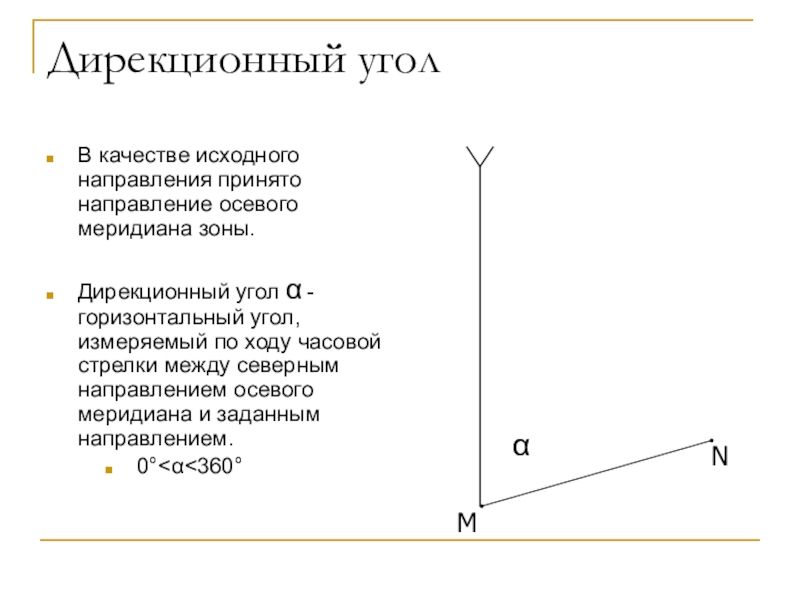
Слайд 33Дирекционный угол
В качестве исходного направления принято направление осевого меридиана зоны.
Дирекционный
угол - горизонтальный угол, измеряемый по ходу часовой стрелки
между северным направлением осевого меридиана и заданным направлением.0360
M
N
Слайд 38Румбы и табличные углы
Румбом называется острый угол, отсчитываемый от ближайшего
направления осевого меридиана до заданного направления.
Численные значения румбов без
указания четвертей называются табличными углами.Слайд 39Балтийская система высот
Высота точки А – это расстояние между нулевой
уровенной поверхностью и уровенной поверхностью точка А, отсчитываемое по отвесной
линии, проходящей через точку.Кронштадский футшток задает нулевую уровенную поверхность для определения высот в России -
Балтийскую систему высот.
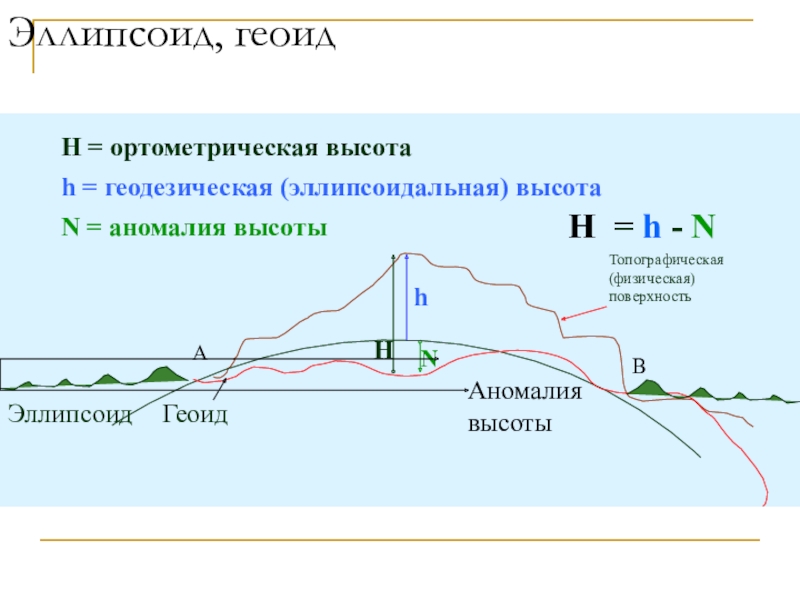
Слайд 43H
H = ортометрическая высота
H =
h - N
Топографическая
(физическая)
поверхность
h = геодезическая (эллипсоидальная) высота
N = аномалия
высотыЭллипсоид, геоид
A
B
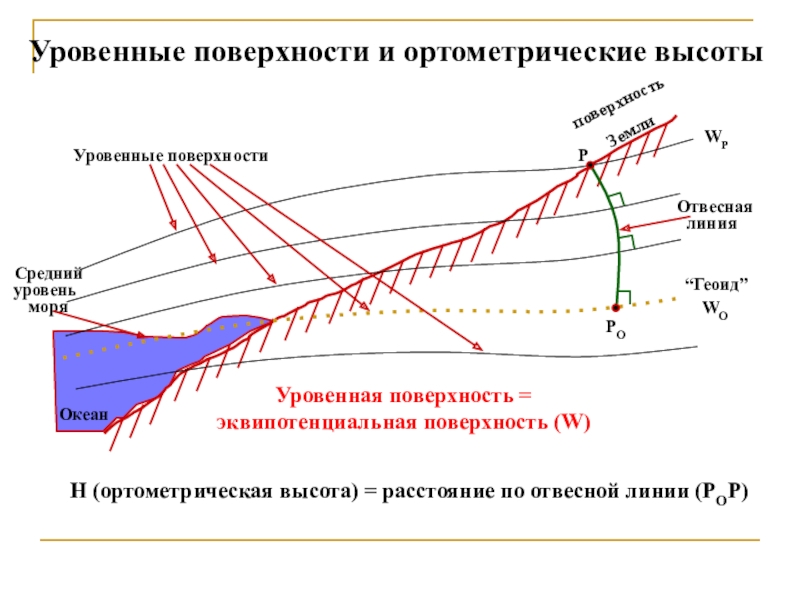
Слайд 44Уровенные поверхности и ортометрические высоты
Уровенные поверхности
Отвесная
линия
“Геоид”
PO
P
Уровенная поверхность = эквипотенциальная поверхность
(W)
H (ортометрическая высота) = расстояние по отвесной линии (POP)
Земли
поверхность
Океан
Средний
уровень
моря
WO
WP
Слайд 52Съемка территории. Составление плана участка местности
Планово-высотное обоснование
Пункты триангуляции и
полигонометрии: точки обозначенные на местности постоянными специальными знаками, имеющими надземную
и подземную часть. Для таких точек установлены их координаты и высоты в единой государственной системе координат (X, Y, H):а) на незастроенной территории;
б) заделка в фасаде здания.
Съемочные точки теодолитных ходов: точки обозначенные на местности временными знаками Для таких точек устанавливают их координаты и высоты (X, Y, H) в процессе съемочных работ.
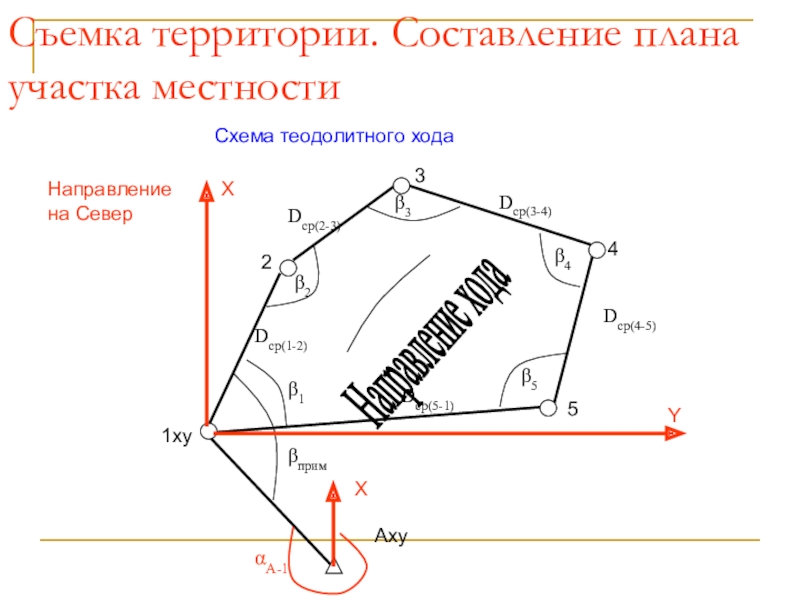
Слайд 53Съемка территории. Составление плана участка местности
Схема теодолитного хода
2
прим
3
4
5
Dср(1-2)
Dср(2-3)
Dср(3-4)
Dср(4-5)
Dср(5-1)
Направление хода
1
Аxy
1xy
2
3
4
5
Направление на
Север
X
Y
αA-1
X
Слайд 549 КЖ
154,7
10,0
8,0
4,2
4,7
14,9
11,9
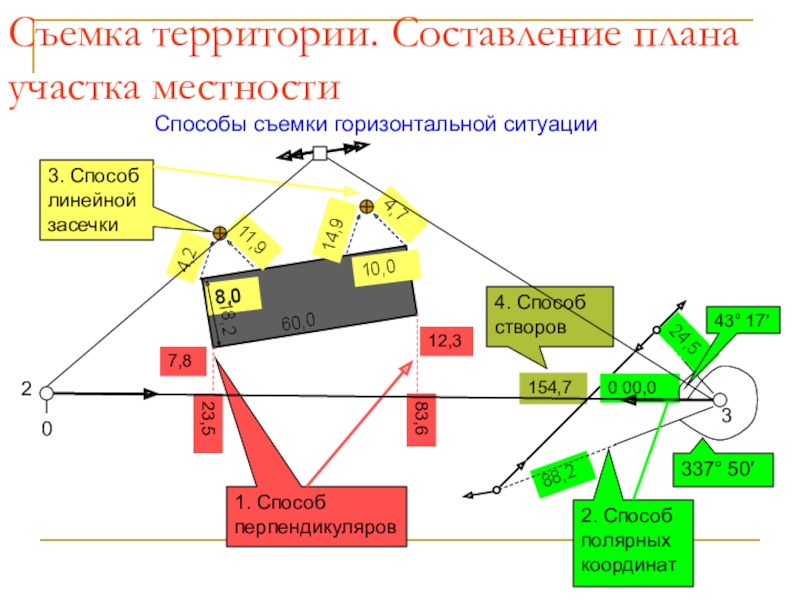
Съемка территории. Составление плана участка местности
Способы съемки горизонтальной ситуации
23,5
7,8
12,3
83,6
60,0
18,2
2
3
0
00,0
24,5
43° 17′
337° 50′
88,2
1. Способ перпендикуляров
3. Способ линейной засечки
2. Способ полярных
координат4. Способ створов
0
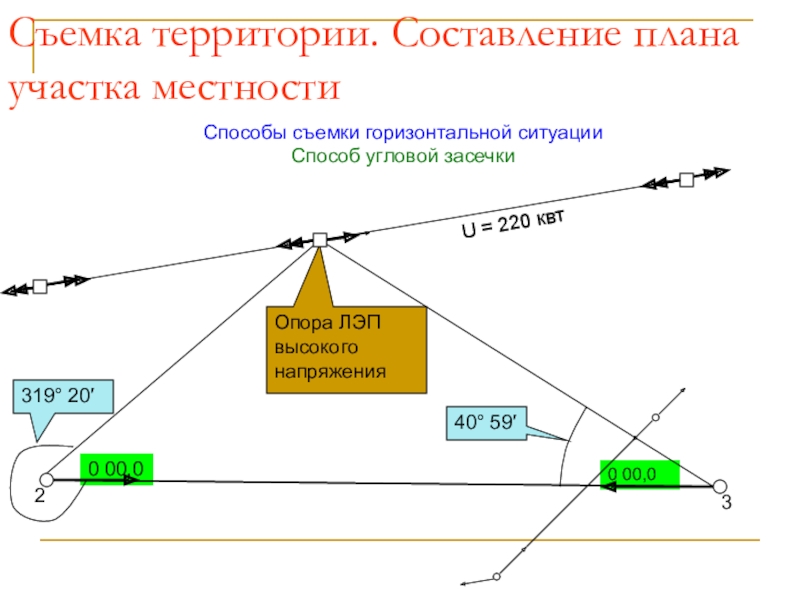
Слайд 55Съемка территории. Составление плана участка местности
Способы съемки горизонтальной ситуации
Способ угловой
засечки
2
3
0 00,0
0 00,0
319° 20′
40° 59′
Опора ЛЭП высокого напряжения
U = 220
квтСлайд 56Съемка территории. Составление плана участка местности
Камеральные работы
Решение обратной геодезической задачи;
Вычисление
горизонтальных углов по результатам полевых измерений;
Вычисление горизонтальных проложений между смежными
точками;Вычисления в ведомости координат:
Исходные данные;
Уравнивание горизонтальных углов;
Вычисление дирекционных углов;
Вычисление приращений координат;
Уравнивание приращений координат;
Вычисление координат точек теодолитного хода.
Вычисления в ведомости геометрического нивелирования:
Исходные данные;
Уравнивание превышений
Вычисление отметок точек нивелирного хода.
Вычисления в журнале тахеометрической съемки:
Исходные данные;
Вычисление отметок пикетов.
Составление плана ситуации и рельефа:
Нанесение ситуации;
Нанесение пикетов и рисовка горизонталей.
Слайд 57Съемка территории. Составление плана участка местности
Вычисления в ведомости координат.
Вычисление
дирекционных углов
С Север
αпред
αпосл
βправ
αпред
180°
С Север
А
В
D
βлев
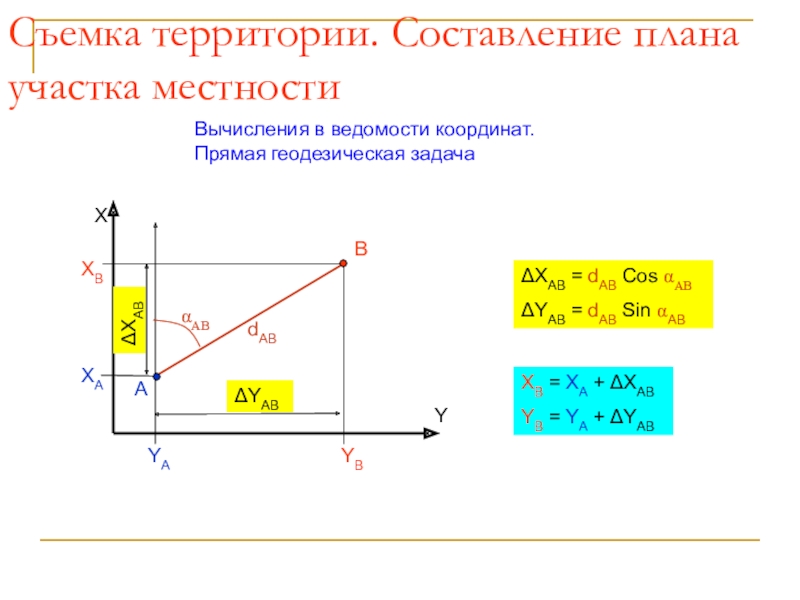
Слайд 58Съемка территории. Составление плана участка местности
Вычисления в ведомости координат. Прямая
геодезическая задача
Y
X
YA
XA
A
B
YB
XB
dAB
αAB
ΔYAB
ΔXAB
ΔXAB = dAB Cos αAB
ΔYAB = dAB Sin αAB
XB
= XA + ΔXAB YB = YA + ΔYAB
Слайд 59Съемка территории. Составление плана участка местности
Вычисление в ведомости координат. Уравнивание
(сторон) приращений координат
Слайд 60Съемка территории. Составление плана участка местности
Вычисление в ведомости координат. Уравнивание
(сторон) приращений координат
Xпосл = Xпред + ΔXиспр
Yпосл = Yпред +
ΔYиспр ΔXиспр = ΔXвыч + vx
ΔXиспр = ΔXвыч + vy
Асолютная погрешность –
Допустимая погрешность –
Поправки в приращения координат –
Исправленные приращения координат –
Координаты точек теодолитного хода –
Слайд 61Съемка территории. Составление плана участка местности
Съемка рельефа
Съемочное обоснование
Геометрическое нивелирование
Тригонометрическое нивелирование
Нивелирование
застроенной территории
Тахеометрическая съемка
Рисовка рельефа на плане
Слайд 62Съемочное обоснование
Геометрическое нивелирование
Схема нивелирного хода
Т 1
Т 2
Т 3
Т 4
Т 5
Рп
10
Рп 11
Направление хода
hср = - 970
hср = -565
hср = +
583hср
hср
hср
Слайд 63Съемочное обоснование
Геометрическое нивелирование
Уравнивание превышений
Исходные данные:
Средние превышения между станциями hср
Сумма средних превышений
от репера № 10 до репера № 11 → hср
Отметки Реперов → Hрп10
→ Hрп11
2 Вычисления:
Фактической невязки: f hф= hср – (HK - HH )
f hф= hср – (Hрп11 - Hрп10 )
Допустимой невязки: fh(доп) =
Поправок в превышения: δh = - f hф/ n
Исправленных превышений: hиспр = hср + δh
Отметок точек: Hi+1 = Hi + hиспр
Слайд 64Тахеометрическая съемка
Полевые работы:
Разбивка и закрепление съемочного обоснования
Измерение магнитного азимута начальной
стороны, горизонтальных, вертикальных углов и расстояний между вершинами.
Съемка ситуации и
рельефа. Слайд 66Порядок работ на станции:
Устанавливают теодолит над вершиной теодолитного хода (например
I). Съемка выполняется при круге лево. Приводят теодолит в рабочее
положение, измеряют его высоту «i», отмечают эту высоту на рейках и записывают в журнал.Ориентируют лимб. Для этого устанавливают по горизонтальному кругу отсчет 0°00', открепляют лимб и визируют на переднюю точку теодолитного хода. Закрепляют лимб.
Открепляют алидаду и визируют на речную точку. Средний штрих сетки нитей совмещают с отмеченной на рейке высотой теодолита «i» и берут отчеты по нитяному дальномеру, по горизонтальному и вертикальному кругу и записывают их в журнал.
После съемки всех реечных точек проверяют ориентирование лимба, для этого визируют на станцию II и берут отчет по горизонтальному кругу. Он должен быть равен 0°00’± 2t.
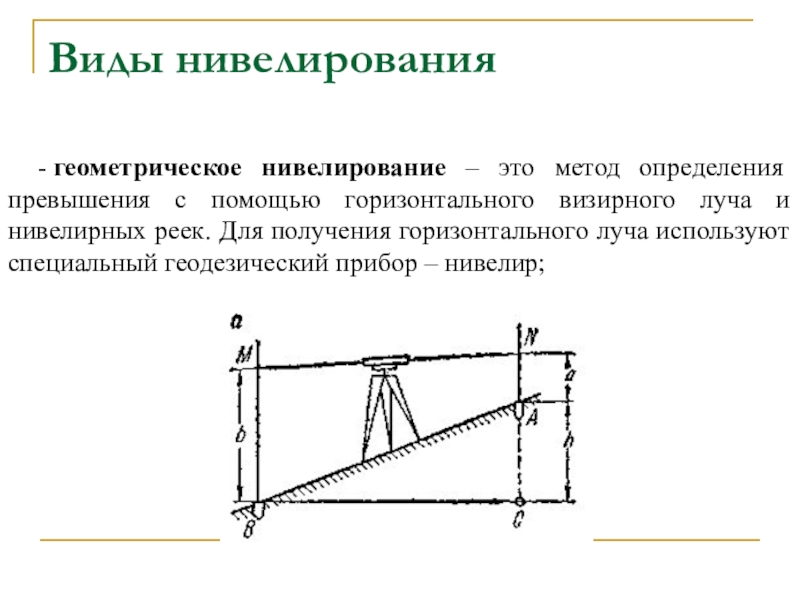
Слайд 67Виды нивелирования
- геометрическое нивелирование – это метод определения превышения с
помощью горизонтального визирного луча и нивелирных реек. Для получения горизонтального
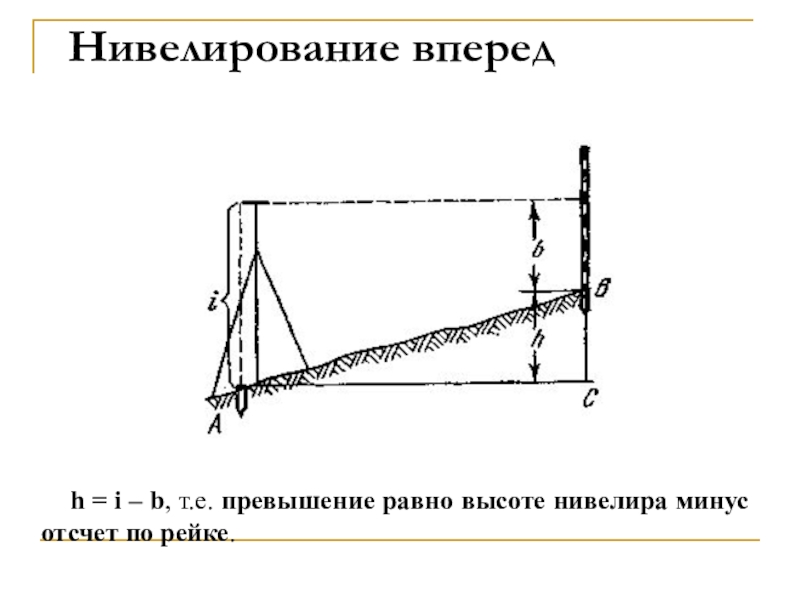
луча используют специальный геодезический прибор – нивелир;Слайд 68Нивелирование вперед
h = i – b, т.е. превышение равно
высоте нивелира минус отсчет по рейке.
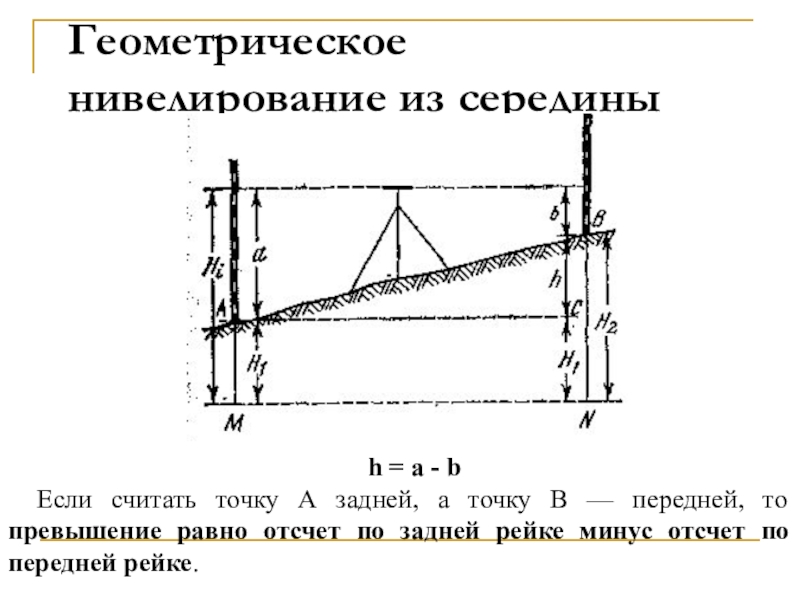
Слайд 69Геометрическое нивелирование из середины
h = a - b
Если считать
точку А задней, а точку В — передней, то превышение
равно отсчет по задней рейке минус отсчет по передней рейке.Слайд 70Зная высоту НА точки А и превышение и над ней
точки В, получают высоту НВ точки В по формуле
НВ =
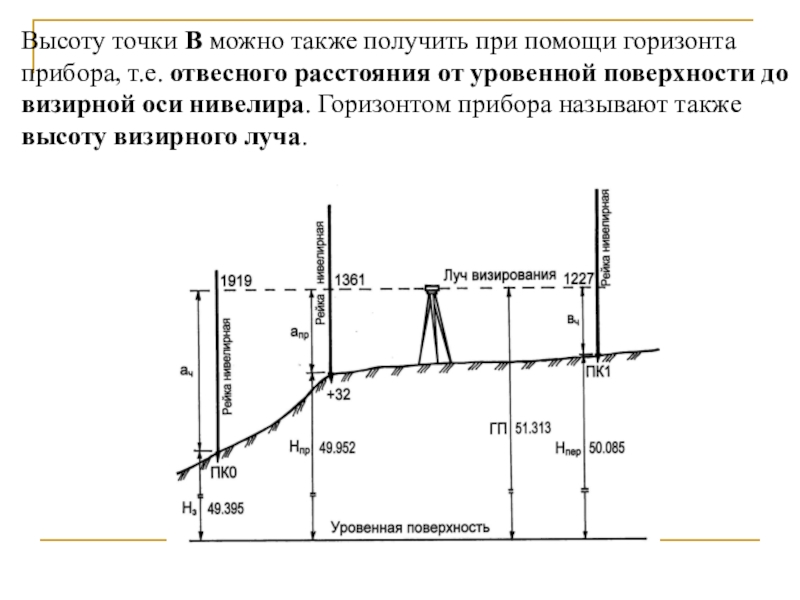
НА + h, т.е. высота последующей точки равна высоте предыдущей точки плюс превышение между ними. Слайд 71Высоту точки В можно также получить при помощи горизонта прибора,
т.е. отвесного расстояния от уровенной поверхности до визирной оси нивелира.
Горизонтом прибора называют также высоту визирного луча.Слайд 72ГП = НА + а, т.е. высоте точки на которой
стоит рейка, плюс отсчет по рейки на нее.
Зная горизонт прибора,
легко найти высоту любой точки, на которую был сделан отсчет по рейке.НВ = ГП – b, высота точки равна горизонту прибора минус отсчет по рейке на этой точке.
Вычислять высоты точек по горизонту прибора удобно, когда были сделаны отсчеты на несколько точек с одной станции.
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть