Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия. Билет №28
Содержание
- 1. Геометрия. Билет №28
- 2. 1. Теорема Стюарта Формулировка теоремы Стюарта: Если точка D
- 3. ДОКАЗАТЕЛЬСТВОВведем прямоугольную систему координат с началом в
- 4. Принимая во внимание: - что, длина отрезка, лежащего
- 5. Следовательно: AС²*DВ+AВ²*СD-AD²*СB=(x²+y²)*(b-d) + [(x-b)²+y²]*d – [(x-d)²+y²]*b Раскрывая скобки и
- 6. 2. Формула Брахмагупты Формула Брахмагупты выражает площадь вписанного
- 7. ДОКАЗАТЕЛЬСТВОЕсли угол D четырёхугольника ABCD обозначить буквой
- 8. Применяя теорему косинусов к треугольнику ACD, получаем:AС²
- 9. Далее, проводим алгебраические действия:Таким образом,Что и Требовалось Доказать.
- 10. Скачать презентанцию
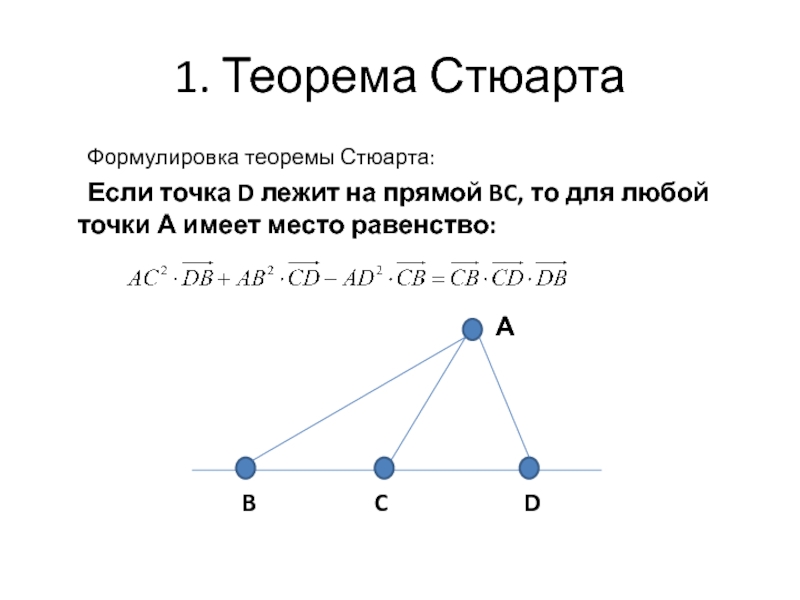
1. Теорема Стюарта Формулировка теоремы Стюарта: Если точка D лежит на прямой BC, то для любой точки А имеет место равенство: АDCB
Слайды и текст этой презентации
Слайд 21. Теорема Стюарта
Формулировка теоремы Стюарта:
Если точка D лежит на прямой
BC, то для любой точки А имеет место равенство:
Слайд 3 ДОКАЗАТЕЛЬСТВО
Введем прямоугольную систему координат с началом в точке С.
Тогда точка
С имеет координаты (0;0).
Следовательно:
- точка В имеет координаты (b;0),
- точка
D имеет координаты (d;0),- точка A имеет координаты (x;y),
где b, d, x, y – некоторые числа.
А (x;y)
D (d;0)
C (0;0)
B (b;0)
x
y
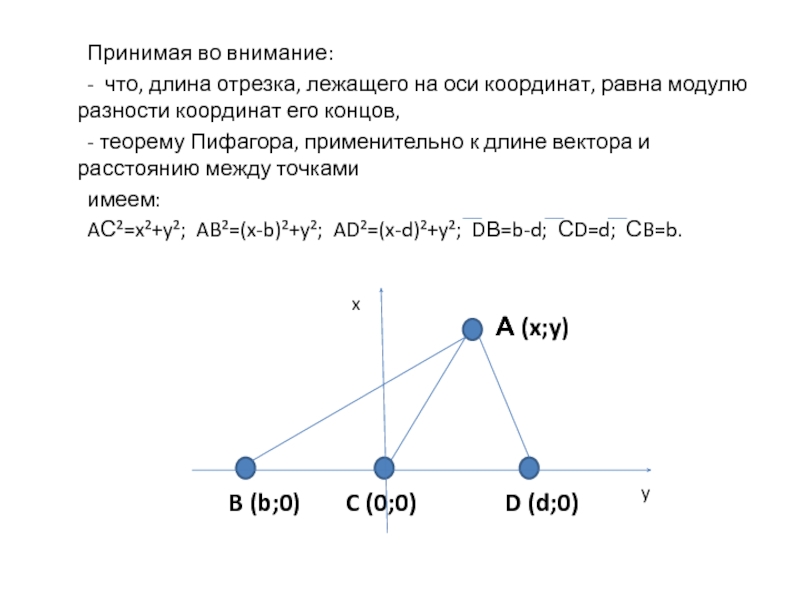
Слайд 4 Принимая во внимание:
- что, длина отрезка, лежащего на оси координат,
равна модулю разности координат его концов,
- теорему Пифагора, применительно к
длине вектора и расстоянию между точкамиимеем:
AС²=x²+y²; AB²=(x-b)²+y²; AD²=(x-d)²+y²; DВ=b-d; СD=d; СB=b.
А (x;y)
D (d;0)
C (0;0)
B (b;0)
x
y
Слайд 5 Следовательно:
AС²*DВ+AВ²*СD-AD²*СB=(x²+y²)*(b-d) + [(x-b)²+y²]*d – [(x-d)²+y²]*b
Раскрывая скобки и работая с подобными
слагаемыми получаем:
AС²*DВ+AВ²*СD-AD²*СB = b*d*(b-d)
Но произведение СB*СD*DВ тоже равно b*d*(b-d),
Что и
Требовалось Доказать.![Следовательно: AС²*DВ+AВ²*СD-AD²*СB=(x²+y²)*(b-d) + [(x-b)²+y²]*d – [(x-d)²+y²]*b Раскрывая скобки и работая с подобными слагаемыми получаем: AС²*DВ+AВ²*СD-AD²*СB = b*d*(b-d) Но произведение СB*СD*DВ тоже](/img/thumbs/776e00ada1fc9c0cb785a6a9b62668f8-800x.jpg "Геометрия. Билет №28 Следовательно: AС²*DВ+AВ²*СD-AD²*СB=(x²+y²)*(b-d) + [(x-b)²+y²]*d – [(x-d)²+y²]*b Раскрывая скобки и работая с подобными слагаемыми")
Слайд 62. Формула Брахмагупты
Формула Брахмагупты выражает площадь вписанного в окружность четырёхугольника
как функцию длин его сторон.
Если вписанный четырёхугольник имеет длины сторон
a, b, c, d и полупериметр p = (a + b + c + d) / 2 , то его площадь равнаявляется общим случаем формулы Герона для треугольников.
a
b
c
d
Слайд 7ДОКАЗАТЕЛЬСТВО
Если угол D четырёхугольника ABCD обозначить буквой φ, то, поскольку
сумма противоположных углов вписанного четырёхугольника равна π, угол B будет
равен π – φ. По этой причине:Следовательно:
Слайд 8Применяя теорему косинусов к треугольнику ACD, получаем:
AС² = a² +
b² - 2ab cos φ.
Применяя теорему косинусов к треугольнику
ABC, получаем:AС² = c² + d² - 2cd cos (π – φ) = c² + d² + 2cd cos φ .
Следовательно,
