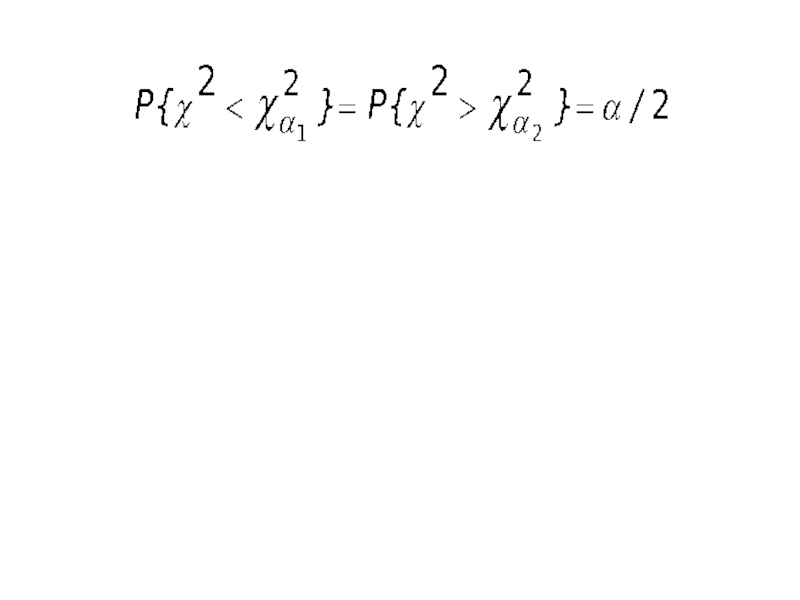Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Глава 8. Интервальное оценивание параметров распределения случайных величин
Содержание
- 1. Глава 8. Интервальное оценивание параметров распределения случайных величин
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. 8.2. Доверительный интервал для математического ожидания нормального распределения
- 7. Рассмотрим оценку математического ожидания mx нормально
- 8. Введем случайную величинукоторая имеет нормированное нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.
- 9. Тогда вероятность Р=1 – того, что
- 10. Принимая во внимание, что функция распределения Ф*(t)
- 11. Для заданной вероятности Р = 1 –
- 12. Таким образом, доверительным интервалом называется такой интервал,
- 13. С увеличением надежности (уменьшением ) доверительный интервал
- 14. Поскольку концы интервала представляют собой случайные величины,
- 15. Теперь рассмотрим оценку математического
- 16. Величинапри этих условиях имеет t-распределение (распределение Стьюдента) с k=n–1.
- 17. Для нахождения доверительного интервала значения mx:задаемся надежностью
- 18. 8.3. Доверительный интервал для дисперсии нормального распределения Рассмотрим
- 19. Для этого используем соотношение:Из указанного отношения можно
- 20. Таким образом, если математическое ожидание неизвестно, то
- 21. Слайд 21
- 22. откуда получаемСледовательно, интервал
- 23. есть доверительный интервал для дисперсии 2 с
- 24. Слайд 24
- 25. Глава 9. Проверка статистических гипотез
- 26. 9.1. Постановка задачи. Основные понятия и определенияВсякое
- 27. СГ являются, например, предположения:1. Закон распределения наблюдаемой
- 28. Простой называют гипотезу, содержащую только одно предположение,
- 29. Замечание. Какая из ошибок является на практике
- 30. С расширением области ошибка
- 31. Статистическим критерием называется случайная величина К с
- 32. Процесс проверки гипотезы состоит из следующих этапов:1)
- 33. kкр располагается критическая область, а слева –
- 34. – левостороннюю критическую область, определяемую неравенством K
- 35. Параметр 1 – равный условной вероятности
- 36. Скачать презентанцию
8.2. Доверительный интервал для математического ожидания нормального распределения
Слайды и текст этой презентации
Слайд 1Глава 8. Интервальное оценивание параметров распределения случайных величин
8.1. Доверительный интервал
Слайд 7
Рассмотрим оценку
математического ожидания mx нормально распределенной случайной величины
Х с известной дисперсией 2.
по нормальному закону, то выборочное среднее будет также распределено по нормальному закону с математическим ожиданием mx и дисперсией 2/n:
Слайд 8
Введем случайную величину
которая имеет нормированное нормальное распределение с нулевым математическим
ожиданием и единичной дисперсией.
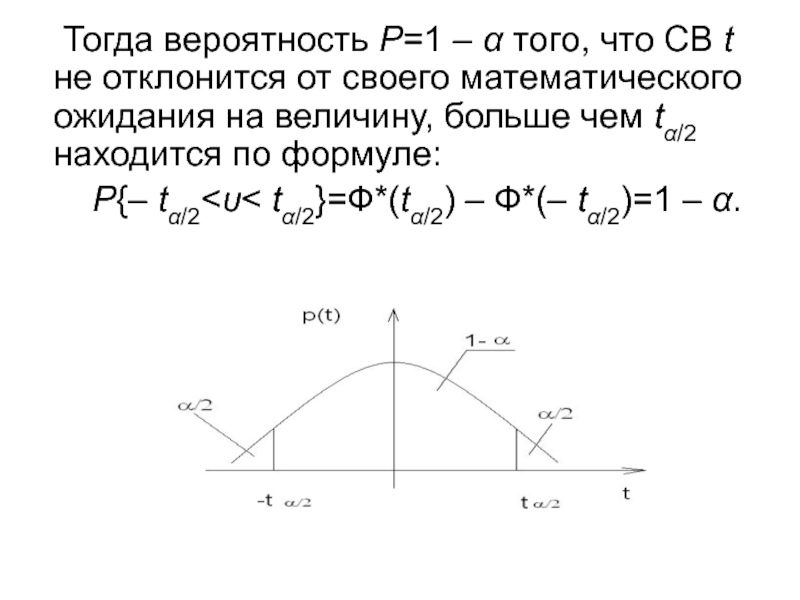
Слайд 9 Тогда вероятность Р=1 – того, что СВ t не
отклонится от своего математического ожидания на величину, больше чем t/2
находится по формуле:Р{– t/2 t/2}=Ф*(t/2) – Ф*(– t/2)=1 – .
Слайд 10Принимая во внимание, что функция распределения Ф*(t) связана с функцией
Лапласа Ф(t) соотношениями:
Ф(t)=0,5+ Ф*(t), Ф(t)=0,5 – Ф*(t), поэтому
Р{– t/2 t/2}=2Ф(t/2)=1
– . Поскольку функция Ф(t) непрерывна и возрастает на интервале [0,) от 0 до 0,5, то для любого числа , удовлетворяющего неравенству 0<1 – <1, существует единственное число t/2 такое, что Ф(t/2)=0,5(1 – ).
Слайд 11Для заданной вероятности Р = 1 – по таблице
значений функции Лапласа Ф(t) можно найти соответствующее значение t/2 .
С надежностью Р=1 – можно утверждать, что доверительный интервал
покрывает неизвестный параметр mx с точностью
Слайд 12Таким образом, доверительным интервалом называется такой интервал, относительно которого можно
с заранее определенной, близкой к 1, вероятностью утверждать, что он
содержит не известное нам истинное значение параметра mx:Из этого соотношения видно что, чем точнее при данном значении мы хотим оценить среднее значение, тем больше n экспериментов необходимо провести.
Слайд 13С увеличением надежности (уменьшением ) доверительный интервал расширяется, т.е. точность
уменьшается. Если задать точность и вероятность , то можно
найти минимальный объем выборки n который обеспечит заданную точность :
Слайд 14Поскольку концы интервала представляют собой случайные величины, то их называют
также доверительными границами. Если величина Х распреде-лена не по нормальному
закону распреде-ления, то поскольку величина представ-ляет собой сумму независимых, одинаково распределенных случайных величин, согласно предельной теореме при достаточно больших n (n 30) ее закон распределения близок к нормальному.
Слайд 15
Теперь рассмотрим оценку
математического ожидания mx нормально
распределенной случайной величины Х с неизвестной дисперсией 2. Для оценивания
дисперсии 2 используем оценку.
Слайд 17Для нахождения доверительного интервала значения mx:
задаемся надежностью Р=1– по таблице
t-распределения для уровня значимости /2 (соответствующего односторонней критической области);
из условия
P{t
Слайд 188.3. Доверительный интервал для дисперсии нормального распределения
Рассмотрим построение доверительного интервала
дисперсии нормально распределенной случайной величины Х при неизвестном математическом ожидании.
Слайд 19Для этого используем соотношение:
Из указанного отношения можно определить величину имеющую
k = n – 1 степеней свободы.
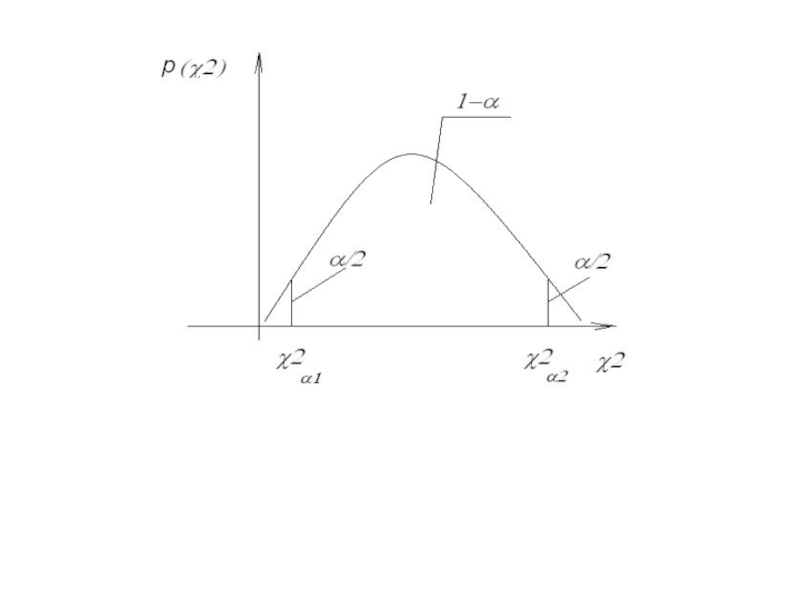
Слайд 20Таким образом, если математическое ожидание неизвестно, то случайная величина 2
распределена по закону 2 с
k = n – 1
степенями свободы. Так как случайная величина 2 неотрицательна, а плотность распределения p(2) несим-метричная (см.рис.), то доверительный интервал будем определять из условияили
Слайд 23есть доверительный интервал для дисперсии 2 с надежностью Р=1 –
, а интервал
представляет собой доверительный интервал для стандартного отклонения
с надежностью Р=1 – . Значения определяем из
таблиц 2 распределения из условия .
Слайд 269.1. Постановка задачи. Основные понятия и определения
Всякое предположение о законе
распределения или параметрах закона распределения СВ Х будем называть статистической
гипотезой (СГ).Задачу установления истинности гипотез по выборке наблюдений будем называть проверкой статистических гипотез.
Слайд 27СГ являются, например, предположения:
1. Закон распределения наблюдаемой СВ является нормальным;
2.
МО наблюдаемой нормально распределенной СВ равно заданному числу;
3. Дисперсия и
МО наблюдаемой нормально распределенной СВ принимают заданные значения.Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.
Слайд 28 Простой называют гипотезу, содержащую только одно предположение, сложной – гипотезу,
состоящую из конечного или бесконечного числа простых гипотез.
Основная задача теории
проверки гипотез состоит в разработке методов построения наиболее подходящих критических и допустимых областей, обеспечивающих наилучшее различение гипотез.При проверке гипотез возникают ошибки двух родов:
– ошибка 1 рода – отклонение истинной гипотезы;
– ошибка 2 рода – принятие ложной гипотезы.
Слайд 29 Замечание. Какая из ошибок является на практике более опасной, зависит
от конкретной задачи.
Например, если проверяется правильность выбора метода лечения
больного, то ошибка первого рода означает отказ от правильной методики, что может замедлить лечение, а ошибка второго рода (применение неправильной методики) чревата ухудшением состояния больного и является более опасной.
Слайд 30 С расширением области ошибка 1 рода растет,
а ошибка 2 рода падает.
Условные вероятности и вероятности
ошибок первого и второго рода соответственно.Основной прием проверки статистических гипотез заключается в том, что по имеющейся выборке вычисляется значение некоторой случайной величины, имеющей известный закон распределения.
Слайд 31 Статистическим критерием называется случайная величина К с известным законом распределения,
служащая для проверки нулевой гипотезы.
Критической областью называют область значений критерия,
при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.
Слайд 32 Процесс проверки гипотезы состоит из следующих этапов:
1) выбирается статистический критерий
К;
2) вычисляется его наблюдаемое значение Кнабл по имеющейся выборке;
3) поскольку
закон распределения К известен, определяется (по известному уровню значимости α) критическое значение kкр, разделяющее критическую область и область принятия гипотезы (например, если р(К > kкр) = α, то справа от
Слайд 33kкр располагается критическая область, а слева – область принятия гипотезы);
4)
если вычисленное значение Кнабл попадает в область принятия гипотезы, то
нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.Различают разные виды критических областей:
– правостороннюю критическую область, определяемую неравенством K > kкр ( kкр > 0);
Слайд 34– левостороннюю критическую область, определяемую неравенством K < kкр (kкр
< 0);
– двустороннюю критическую область, определяемую неравенствами K < k1,
K > k2 (k2 > k1).Параметр называют уровнем значимости или размером критерия проверки гипотезы Hi (размером критической области ).
Слайд 35 Параметр 1 – равный условной вероятности отклонения гипотезы Hi
, когда она ошибочна, называют мощностью критерия ее проверки.
Вероятности
и связаны между собой через область критическую область . С возрастанием параметр уменьшается, и наоборот, уменьшению соответствует возрастание .
