Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГРАФИКИ И ОПИСАТЕЛЬНАЯ СТАТИСТИКА
Содержание
- 1. ГРАФИКИ И ОПИСАТЕЛЬНАЯ СТАТИСТИКА
- 2. Методы исследования
- 3. Методы исследования
- 4. Описательная статистика Методы и способы, используемые
- 5. Описательная статистикаЧастотные распределения и графикиМеры центральной тенденцииМеры изменчивостиМеры формы…
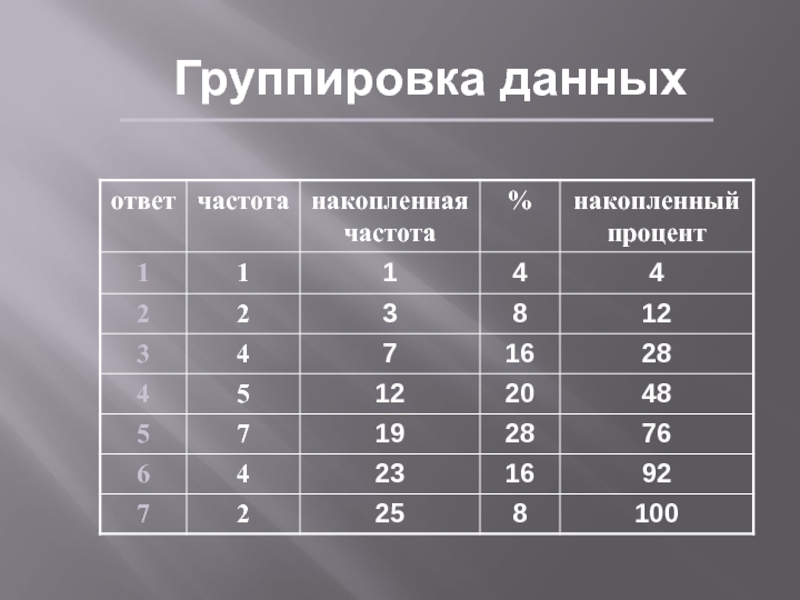
- 6. Группировка данныхПредположим, мы спрашивали студентов, насколько их
- 7. Группировка данныхГипотетические данные опроса 25 студентов: 3,5,6,5,2,3,6,4,6,7,6,4,5,5,1,2,5,4,4,5,5,7,3,3,41,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
- 8. Группировка данных 1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
- 9. Группировка данных
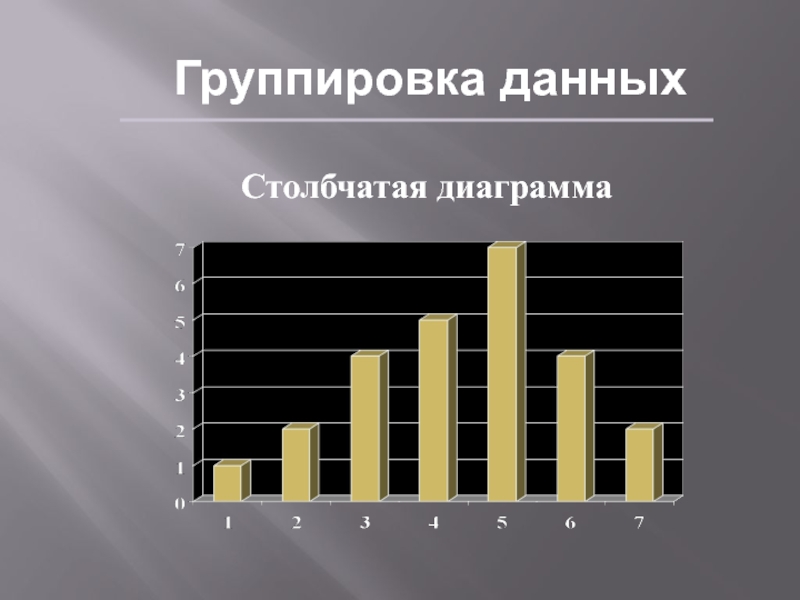
- 10. Группировка данныхСтолбчатая диаграмма
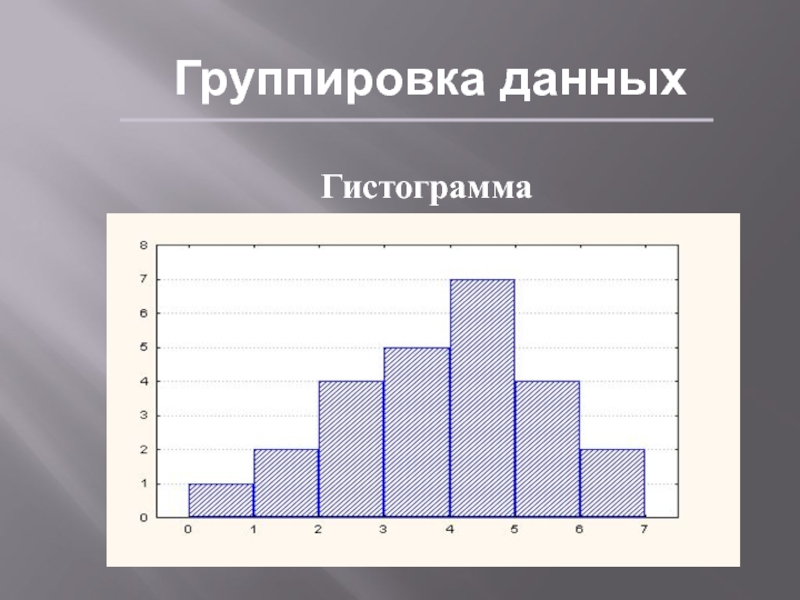
- 11. Группировка данныхГистограмма
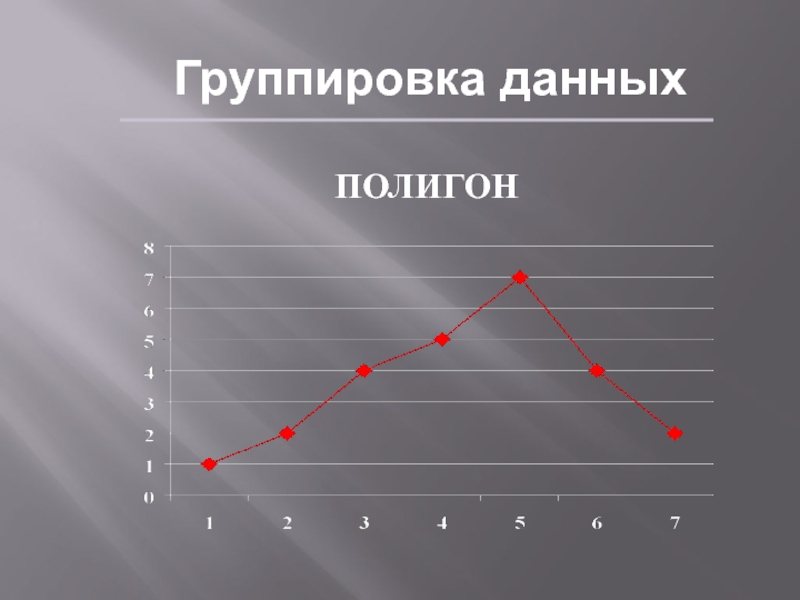
- 12. Группировка данныхПОЛИГОН
- 13. Группировка данных
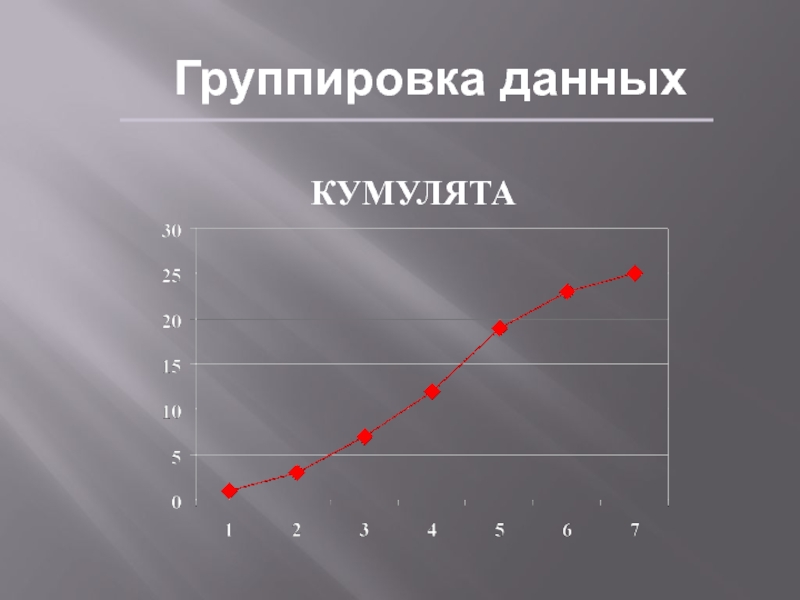
- 14. Группировка данныхКУМУЛЯТА
- 15. Группировка данныхА если значений много?40, 48, 11,
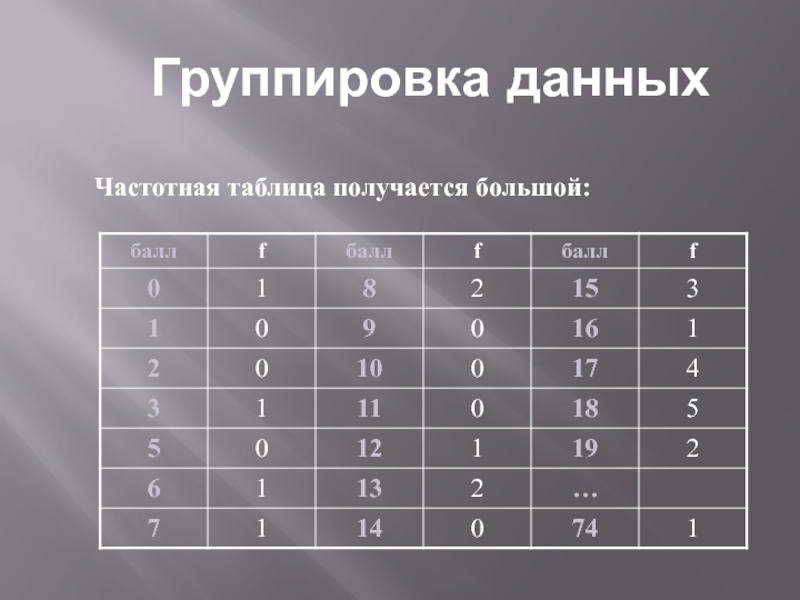
- 16. Группировка данныхЧастотная таблица получается большой:
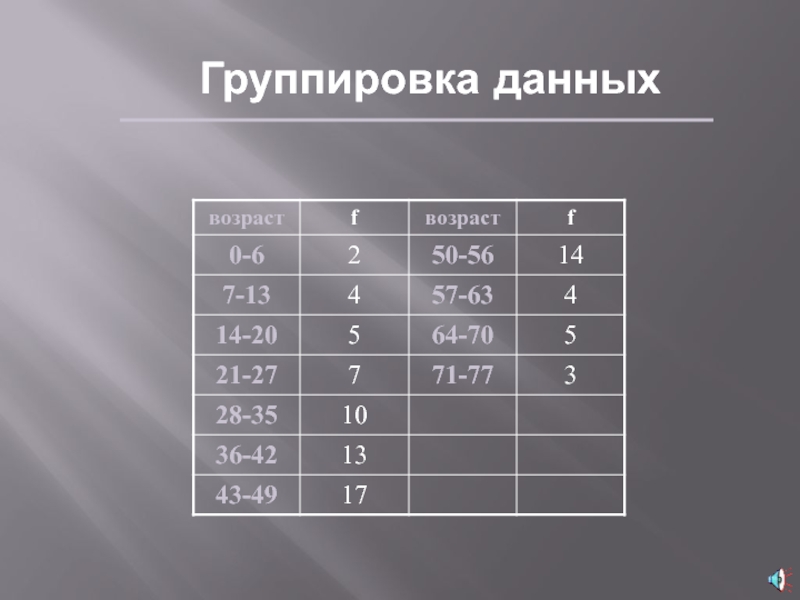
- 17. Группировка данныхТогда стоит сгруппировать значения переменной в
- 18. Группировка данных
- 19. Использование графиков
- 20. Использование графиков
- 21. Использование графиков
- 22. Использование графиков Lie factor – отношение
- 23. Использование графиков Следует избегать соединения изменений в оформлении графика с изменениями в данных
- 24. Использование графиков Еще одна проблема –
- 25. Использование графиков
- 26. Основные понятияВыборочной совокупностью или просто выборкой называют
- 27. Основные понятияПараметры – это меры описания, полученные
- 28. Генеральная и выборочная совокупностиГенеральная совокупность
- 29. ВыборкиВыборки бывают разные!Классификация Л.Мюллера и К. ШусслераПо
- 30. ВыборкиКлассификация Л.Мюллера и К. Шусслера1) Не случайные
- 31. ВыборкиКлассификация Л.Мюллера и К. Шусслера1) Не случайные1.1) Бессистемная выборка1.2) Доступная выборка1.3) Целенаправленная выборка
- 32. ВыборкиКлассификация Л.Мюллера и К. Шусслера1.1) Бессистемная выборка
- 33. ВыборкиКлассификация Л.Мюллера и К. Шусслера1.2) Доступная выборка
- 34. ВыборкиКлассификация Л.Мюллера и К. Шусслера1.3) Целенаправленная выборка
- 35. ВыборкиКлассификация Л.Мюллера и К. Шусслера2) Случайные2.1) Простая случайная2.2) Серийная2.3) Систематическая (интервальная)2.4) Стратифицированная2.5) Комбинированная
- 36. ВыборкиКлассификация Л.Мюллера и К. Шусслера2.1) Простая случайная
- 37. ВыборкиКлассификация Л.Мюллера и К. Шусслера2.2) Серийная –
- 38. ВыборкиКлассификация Л.Мюллера и К. Шусслера2.3) Систематическая (интервальная)
- 39. ВыборкиКлассификация Л.Мюллера и К. Шусслера2.4) Стратифицированная выборка
- 40. ВыборкиКлассификация Л.Мюллера и К. Шусслера2.5) Комбинированная –
- 41. Меры центральной тенденции Среднее арифметическое (М или
- 42. Меры центральной тенденции Среднее арифметическоеM=(x1+…+xN)/N 1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7М=(1+2+2+3+3+….+6+7+7)/25=4,4
- 43. Меры центральной тенденции Медиана Me1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7прибавляем 1 к
- 44. Меры центральной тенденции1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7А что же делать, когда
- 45. Меры центральной тенденцииМодаМd=51,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
- 46. Доверительный интервалДоверительный интервал(95% confidence limits of mean)
- 47. Доверительный интервалЕсли среднее выборки равно 23, а
- 48. Меры изменчивостиРазмах ДисперсияСтандартное (среднеквадратичное) отклонениеСтандартная ошибка
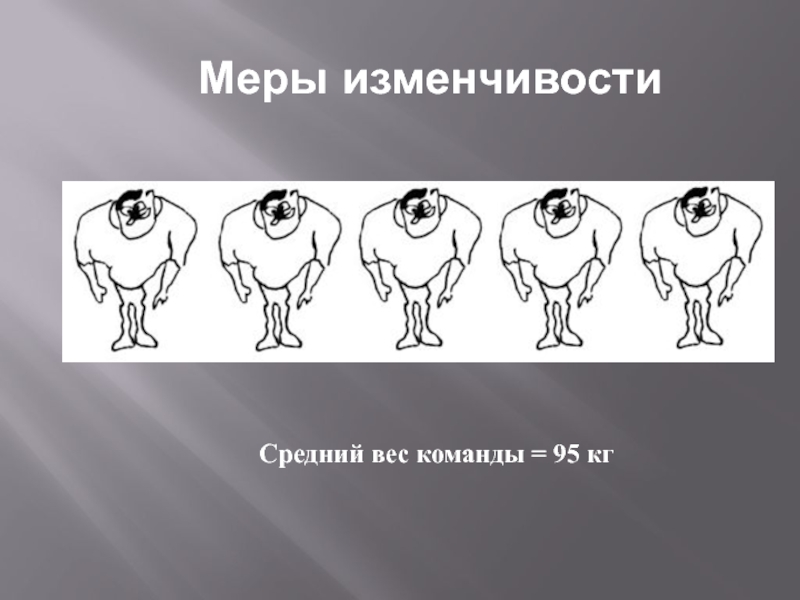
- 49. Меры изменчивостиСредний вес команды = 95 кг
- 50. Меры изменчивостиСредний вес команды тоже = 95 кг
- 51. Меры изменчивостиРазмах R = Xmax- Xmin 1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7R = Xmax– Xmin=7-1=6
- 52. Меры изменчивостиДисперсия
- 53. Меры изменчивостиПример. Вычислить дисперсию для следующей выборки:5,
- 54. Меры изменчивостиПодставляем в формулу:
- 55. Меры изменчивостиДругая формула для дисперсии:
- 56. Меры изменчивостиСтандартное отклонение
- 57. Меры изменчивостиСтандартная ошибка среднего значения - это
- 58. Меры изменчивостиВ диапазоне удвоенной стандартной ошибки по
- 59. Меры формыАсимметрия является мерой несимметричности распределения. Если
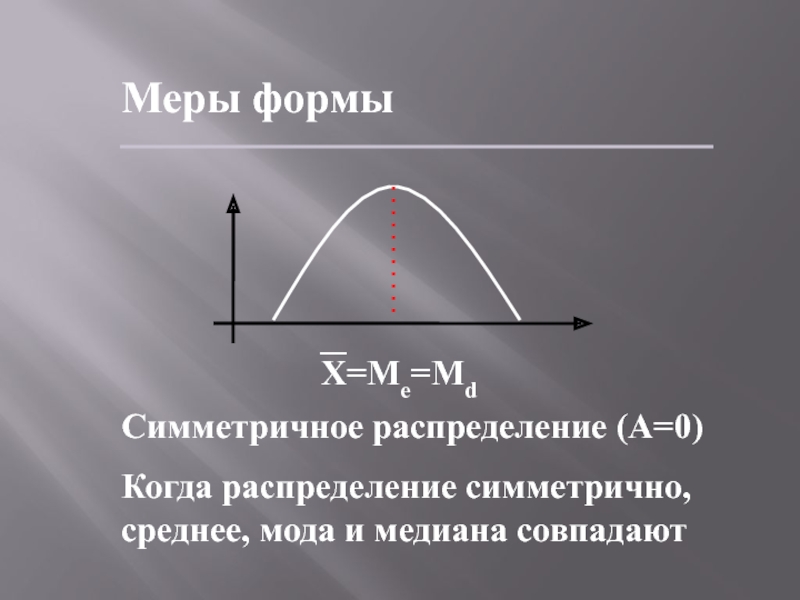
- 60. Меры формыСимметричное распределение (А=0)Когда распределение симметрично, среднее, мода и медиана совпадают Х=Ме=Md
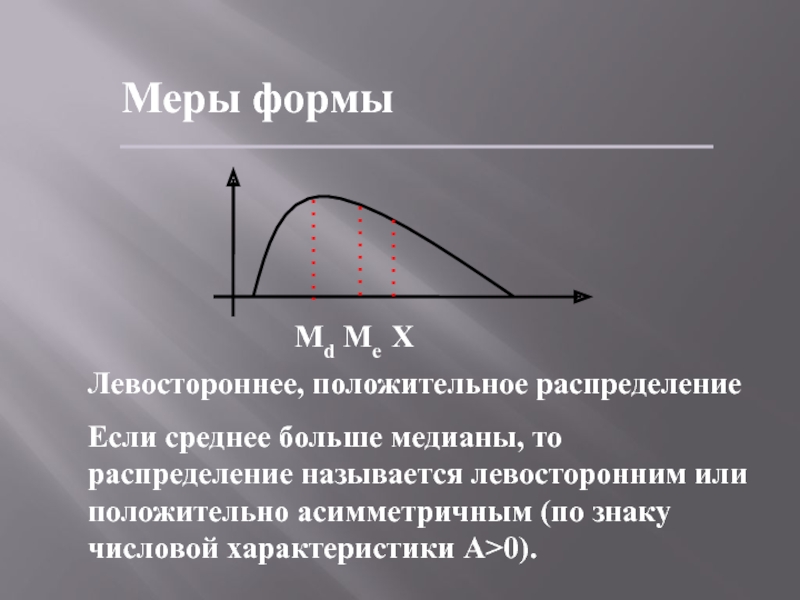
- 61. Меры формыЛевостороннее, положительное распределение Если среднее больше
- 62. Меры формыОтрицательное, правостороннее распределение Если среднее меньше медианы, то распределение называется правосторонним или отрицательно асимметричным (A
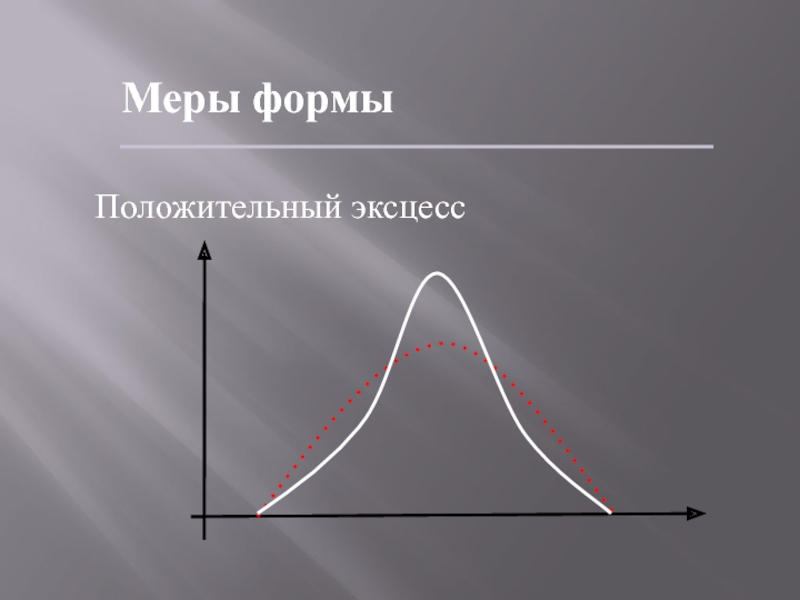
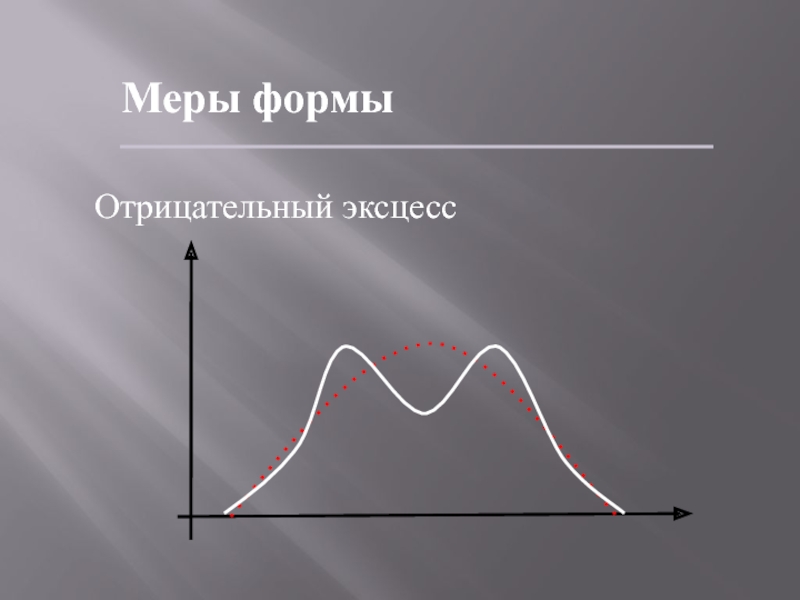
- 63. Меры формыЭксцесс измеряет остроту пика распределения Е=
- 64. Меры формыПоложительный эксцесс
- 65. Меры формыОтрицательный эксцесс
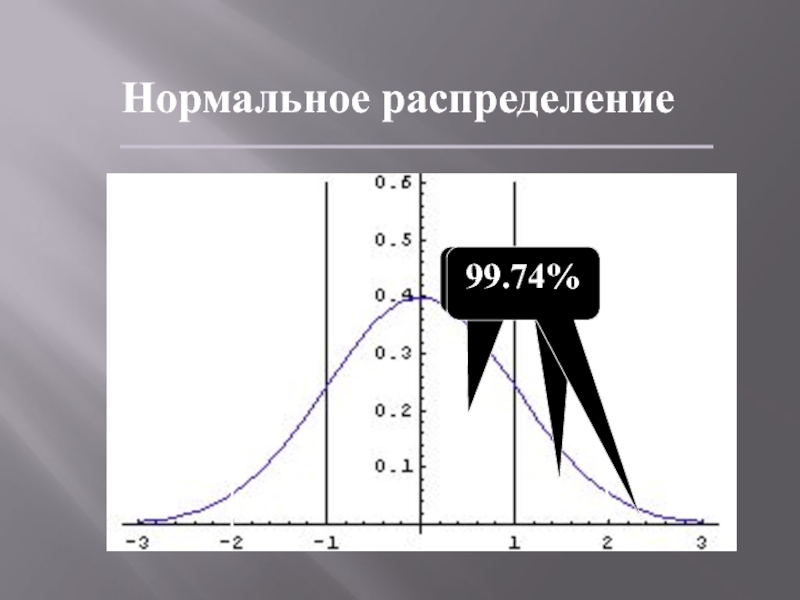
- 66. Нормальное распределениеНормальное распределение: f(x)=(1/2)exp{(x-m)2/22}cреднее значение mдисперсия 2асимметрия
- 67. Нормальное распределение
- 68. Нормальное распределение68.26%95.44%99.74%
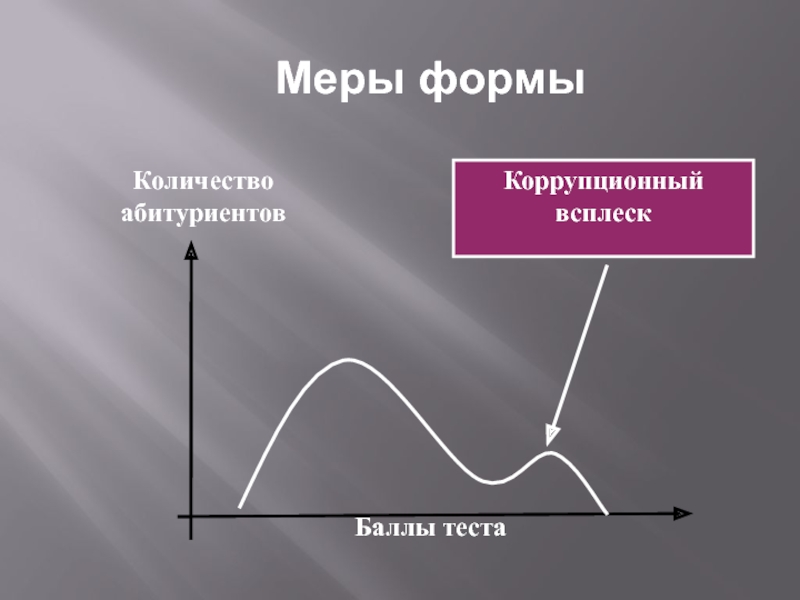
- 69. Меры формыКоррупционный всплескБаллы тестаКоличество абитуриентов
- 70. Нормальное распределениеНормальная кривая человеческих достижений:2 года –
- 71. Какую меру выбрать?
- 72. Какую меру выбрать?Медиана используется когда 1) распределение
- 73. Что мы должны знать?Как строить частотные таблицы
- 74. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Описательная статистика
Методы и способы, используемые для «суммирования», организации
и «уменьшения» большого количества наблюдений (статистических опытов).
Слайд 5Описательная статистика
Частотные распределения и графики
Меры центральной тенденции
Меры изменчивости
Меры формы
…
Слайд 6Группировка данных
Предположим, мы спрашивали студентов, насколько их провал на экзамене
зависел от причин, которые они никак не могли контролировать.
Ответы
даются по шкале от 1 до 7 (1 - совсем не зависел, 7 - полностью зависел)
Гипотетические данные опроса 25 студентов:
3,5,6,5,2,3,6,4,6,7,6,4,5,5,1,2,5,4,4,5,5,7,3,3,4
Слайд 7Группировка данных
Гипотетические данные опроса 25 студентов:
3,5,6,5,2,3,6,4,6,7,6,4,5,5,1,2,5,4,4,5,5,7,3,3,4
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
Слайд 15Группировка данных
А если значений много?
40, 48, 11, 16, 52, 64,
21, 33, 39, 69, 45, 8,35, 22, 57, 74, 13,
25, 47, 27, 38, 43, 15, 33, 66, 52, 47, 37, 0, 24, 43, 61, 35, 29, 52, 40, ….Слайд 17Группировка данных
Тогда стоит сгруппировать значения переменной в интервалы
1. Найти разницу
между наибольшим и наименьшим значением
и прибавить к ней 1
(74-0)+1=75
2.
Разделить ответ на число выбранных интервалов и округлить до ближайшего нечетного числаi=75/10=7.5 7
3. К самому маленькому значению переменной прибавить i-1
0+i-1=0+7-1=6
Первый интервал будет от 0 до 6
4. Следующий интервал начинается с числа, которое следует за наибольшим значением предыдущего интервала
7+i-1=7+7-1=13
Второй интервал будет от 7 до 13
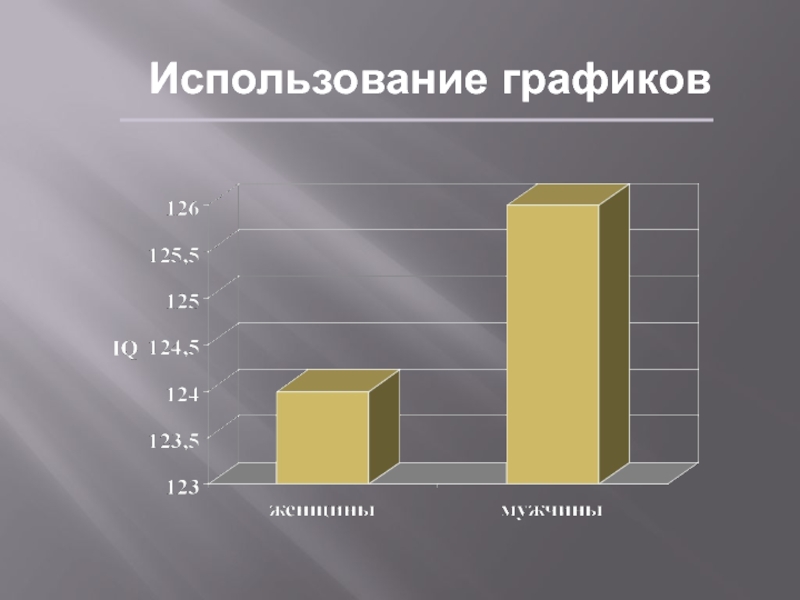
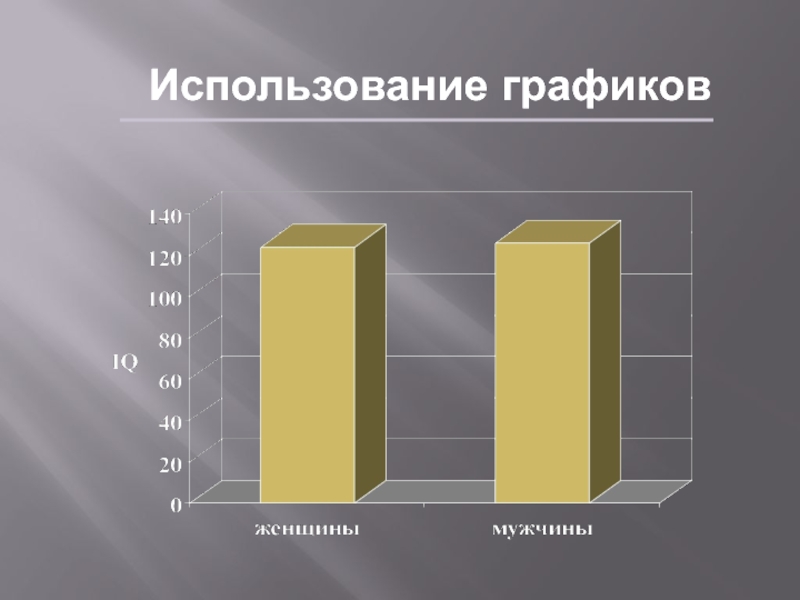
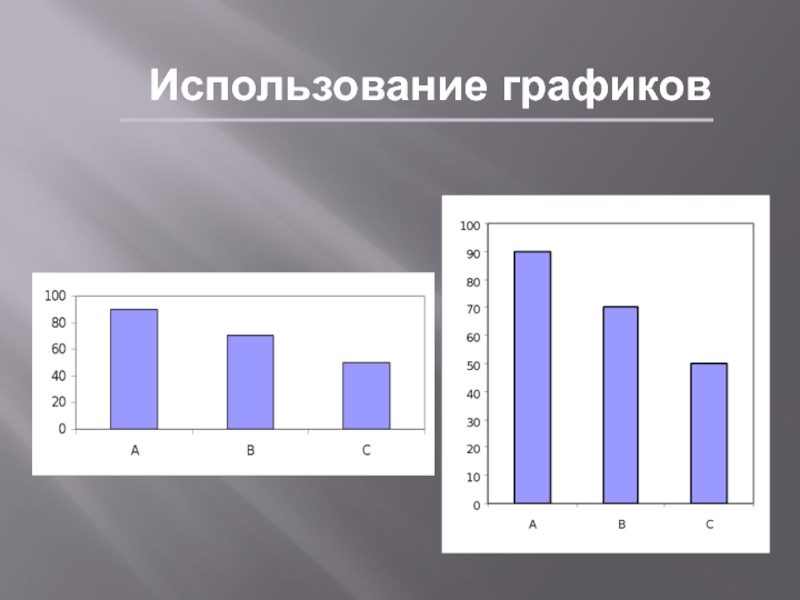
Слайд 22Использование графиков
Lie factor – отношение разницы в размере элементов графика
к разнице величин, которые они представляют
Наиболее информативные («честные») графики имеют
Lie factor =1Слайд 23Использование графиков
Следует избегать соединения изменений в оформлении графика с изменениями
в данных
Слайд 24Использование графиков
Еще одна проблема – многомерные изменения, т.е. изменения сразу
по нескольким размерностям, например, по высоте и ширине.
Если масштабирование ведется
сразу по двум измерениям, площадь изменяется пропорционально квадрату изменений!Слайд 26Основные понятия
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных
объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Слайд 27Основные понятия
Параметры – это меры описания, полученные при сплошном описании
(описании генеральной совокупности).
Статистики (или оценки параметров) – это те же
меры, но полученные при выборочном наблюдении (т.е. параметры описывают генеральную совокупность, а статистики – ее выборку). Слайд 29Выборки
Выборки бывают разные!
Классификация Л.Мюллера и К. Шусслера
По критерию методов отбора
выборки бывают
1) Не случайные
2) Случайные (вероятностные, пробабилистские)
Слайд 30Выборки
Классификация Л.Мюллера и К. Шусслера
1) Не случайные – не имеют
теоретико-вероятностного обоснования и, следовательно, не соответствуют критерию репрезентативности, т.е. статистики
не могут выступать оценками генеральной совокупностиСлайд 31Выборки
Классификация Л.Мюллера и К. Шусслера
1) Не случайные
1.1) Бессистемная выборка
1.2) Доступная
выборка
1.3) Целенаправленная выборка
Слайд 32Выборки
Классификация Л.Мюллера и К. Шусслера
1.1) Бессистемная выборка
Отбор любых
случайно встретившихся прохожих, согласившихся принять участие в исследовании.
Может
использоваться только для самого первого ознакомления с проблемной ситуациейСлайд 33Выборки
Классификация Л.Мюллера и К. Шусслера
1.2) Доступная выборка
Формируется из
числа лиц, которые по субъективным и объективным факторам могут быть
включены в число респондентов, т.е. доступны физически.Используется для накопления данных о латентных или аномальных явлениях
Слайд 34Выборки
Классификация Л.Мюллера и К. Шусслера
1.3) Целенаправленная выборка
Преднамеренный отбор
определенной категории респондентов, которые по оценке исследователя в наибольшей степени
информированы по проблеме или заинтересованы в ее изученииИспользуется в экспертных опросах, лабораторных исследованиях и социальных экспериментах
Слайд 35Выборки
Классификация Л.Мюллера и К. Шусслера
2) Случайные
2.1) Простая случайная
2.2) Серийная
2.3) Систематическая
(интервальная)
2.4) Стратифицированная
2.5) Комбинированная
Слайд 36Выборки
Классификация Л.Мюллера и К. Шусслера
2.1) Простая случайная – формируется путем
случайного отбора единиц наблюдения из однородной генеральной совокупности (жребий, таблицы
случайных чисел, компьютерное моделирование).
Слайд 37Выборки
Классификация Л.Мюллера и К. Шусслера
2.2) Серийная – единицами отбора являются
статистические серии (таксоны, гнезда) – территориальные общности, коллективы, семьи и
т.д. Серии выбираются по методике простой случайной выборкиСлайд 38Выборки
Классификация Л.Мюллера и К. Шусслера
2.3) Систематическая (интервальная) – отбор единиц
производится через один и тот же интервал, при этом начало
отсчета определяется случайным образомСлайд 39Выборки
Классификация Л.Мюллера и К. Шусслера
2.4) Стратифицированная выборка на основе предварительного
выделения в генеральной совокупности однородных частей, типических групп (страт). В
каждой страте производится случайный отбор единиц наблюдения, как правило, пропорционально их доле в генеральной совокупности.Слайд 40Выборки
Классификация Л.Мюллера и К. Шусслера
2.5) Комбинированная – выборка, в которой
используются различные способы отбора.
Например: Гнездовая выборка – по два
предприятия из типичных групп (сильных, средних и слабых). Далее отбор респондентов осуществляется интервальным методом.Слайд 41Меры центральной тенденции
Среднее арифметическое (М или х)
Медиана Me
или срединное значение
Мода Md (наиболее вероятное значение)
Слайд 42Меры центральной тенденции
Среднее арифметическое
M=(x1+…+xN)/N
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
М=(1+2+2+3+3+….+6+7+7)/25=4,4
Слайд 43Меры центральной тенденции
Медиана Me
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7,7
прибавляем 1 к числу значений (размеру
выборки) и делим на 2. Затем определяет значение, которое соответствует
вычисленной позиции в последовательности значений.(25+1)/2=13
Me=5
Слайд 44Меры центральной тенденции
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7
А что же делать, когда у нас четное
число значений? В этом случае медиана - это значение, которое
приходится как раз посередине двух срединных значений. (24+1)/2=12,5значит, значение медианы будет между 12-й и 13-й позицией
Me=(4+5)/2=4,5
Слайд 46Доверительный интервал
Доверительный интервал
(95% confidence limits of mean)
для среднего представляет
интервал значений вокруг оценки, где с данным уровнем доверия находится
«истинное» (неизвестное) среднее генеральной совокупности.Слайд 47Доверительный интервал
Если среднее выборки равно 23, а нижняя и верхняя
границы доверительного интервала с уровнем p=.95 равны 19 и 27
соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее генеральной совокупности.Слайд 48Меры изменчивости
Размах
Дисперсия
Стандартное (среднеквадратичное) отклонение
Стандартная ошибка
Слайд 51Меры изменчивости
Размах R = Xmax- Xmin
1,2,2,3,3,3,3,4,4,4,4,4,5,5,5,5,5,5,5,6,6,6,6,7
R = Xmax–
Xmin=7-1=6
Слайд 53Меры изменчивости
Пример. Вычислить дисперсию для следующей выборки:
5, 6, 3, 8,
5, 9
Вычисляем среднее арифметическое: = (5+6+3+8+5+9)/6=6
Слайд 57Меры изменчивости
Стандартная ошибка среднего значения - это стандартное отклонение, деленное
на квадратный корень из объема выборки.
Слайд 58Меры изменчивости
В диапазоне удвоенной стандартной ошибки по обе стороны от
среднего значения с вероятностью примерно 95% находится среднее значение генеральной
совокупности.Слайд 59Меры формы
Асимметрия является мерой несимметричности распределения. Если этот коэффициент значительно
отличается от 0, распределение является асимметричным
А=
Слайд 60Меры формы
Симметричное распределение (А=0)
Когда распределение симметрично, среднее, мода и медиана
совпадают
Х=Ме=Md
Слайд 61Меры формы
Левостороннее, положительное распределение
Если среднее больше медианы, то распределение
называется левосторонним или положительно асимметричным (по знаку числовой характеристики А>0).
Md Ме Х
Слайд 62Меры формы
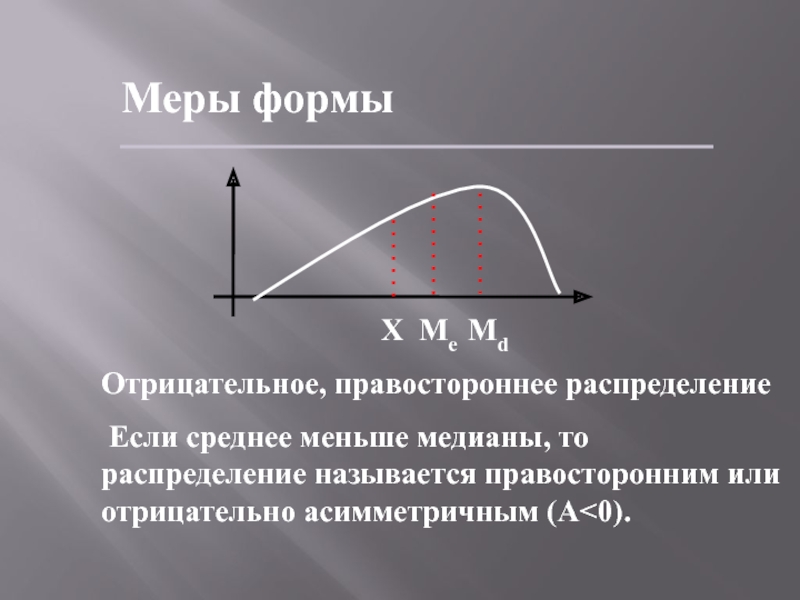
Отрицательное, правостороннее распределение
Если среднее меньше медианы, то
распределение называется правосторонним или отрицательно асимметричным (A
Слайд 66Нормальное распределение
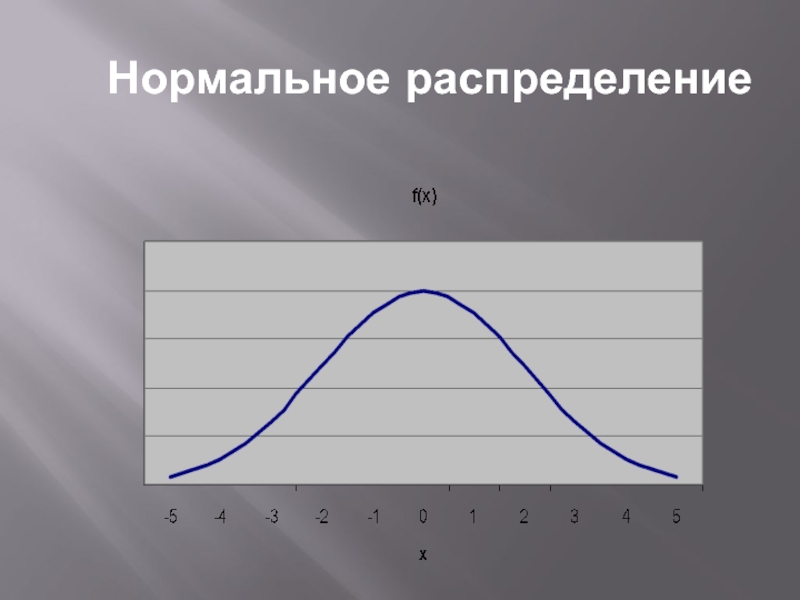
Нормальное распределение:
f(x)=(1/2)exp{(x-m)2/22}
cреднее значение m
дисперсия 2
асимметрия А = 0
эксцесс Е
= 3
Стандартное нормальное распределение имеет нулевое среднее и единичную дисперсию
Слайд 70Нормальное распределение
Нормальная кривая человеческих достижений:
2 года – не писать в
штаны
10 лет – иметь много друзей и много тусоваться
20 лет
– иметь сексуальные отношения30 лет – много зарабатывать и иметь крутую тачку
50 лет – много зарабатывать и иметь крутую тачку
60 лет – иметь сексуальные отношения
70 лет – иметь много друзей и много тусоваться
78 лет – не писать в штаны
Слайд 72Какую меру выбрать?
Медиана используется когда
1) распределение асимметрично
2) есть опасность
перекоса из-за экстремальных значений. Медиана не чувствительна к экстремальным значениям,
в то время как среднее очень чувствительно.3)медиану можно вычислять для данных шкалы порядка и выше.