Графики тригонометрических функций и их свойства

ее свойства
Функция у = cos x
Преобразование графиков тригонометрических

функций путем параллельного переноса
Преобразование графиков тригонометрических функций путем сжатия и расширения
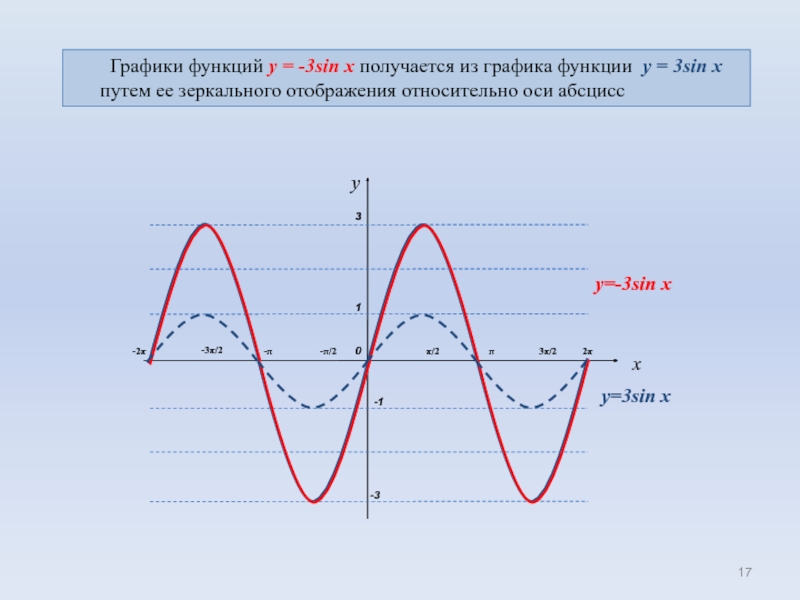
Преобразование графиков тригонометрических функций путем зеркального отражения относительно оси абсцисс
Построение графика функции гармонических колебаний
y=A sin(ωx+φ0)
Построение графика y=sin x с помощью числового круга

x)
Нули функции:
у=0, sin x=0 при х

= pn, nÎZ

Графиком функции y=sin x является синусоида

y=sin x

p+2pn), nÎZ
У

nÎZ

6. Промежутки монотонности:
функция возрастает на промежутках
вида: [-p/2+2pn; p/2+2pn], nÎZ
функция убывает на промежутках
вида: [p/2+2pn; 3p/2+2pn], nÎZ

0

1

π/2

π

-π

x

-π/2

-1

3π/2

2π

-3π/2

-2π

y

0

1

π/2

π

-π

x

-π/2

-1

3π/2

2π

-3π/2

-2π

y

y=sin x

y=sin x

x
Функция y=cos x

при х = 1/2pn, nÎZ
5. Промежутки знакопостоянства:
У>0 при х Î

(-p/2+2pn; p/2+2pn), nÎZ
У<0 при x Î (p/2+2pn; 3p/2+2pn), nÎZ
6. Промежутки монотонности:
функция возрастает на промежутках вида:
[p+2pn; 2p+2pn], nÎZ
функция убывает на промежутках вида:
[0+2pn; p+2pn], nÎZ
7. Точки экстремума:
Хмах= 0 +2pn, nÎZ
Хмin = p +2pn, nÎZ

Свойства функции y=cos x

f (x+в) получается из графика функции
у = f(x)

параллельным переносом на (-в) единиц вдоль оси абсцисс
График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат

по оси абсцисс на расстояние π/4
y=sin (x+ π/4)

y=sin(x) на расстояние π единиц вдоль оси ординат

=k f (x) получается из графика функции у =

f(x) путем его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0

у = sin x путем его растяжения в

3 раза вдоль оси ординат

y=3sin x

функции у = sin x путем его сжатия в

2 раза вдоль оси ординат

-0.5

0.5

y=0.5 sin x

= f (kx) получается из графика функции
у

= f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции
у = f(x) путем его растяжения в k раз (при 0

из графика функции у = cos x путем его растяжения

в 2 раза (0

Видно, что период (T) функции увеличился в 2 раза, т.к. T = 2 π/ω,
где ω – коэффициент при переменной x (частота колебаний)

T = 2 π

T = 4 π

из графика функции у = cos x путем его

сжатия в 2 раза (k>1) вдоль оси абсцисс

T = 2 π

T = 2 π

Видно, что период (T) функции уменьшился в 2 раза, т.к. T = 2 π/ω,
где ω – коэффициент при переменной x (частота колебаний)

функций у = -f (kx) и у=-k f(x) получаются из

графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)

графика функции y = 3sin x путем ее зеркального отображения

относительно оси абсцисс

графика функции
y = 2cos x путем ее зеркального отображения

относительно оси абсцисс

график функции y=3 sin (2x+π/3).
Здесь амплитуда колебаний А равняется 3

единицам,
круговая частота колебаний ω равна 2,
а начальная фаза колебаний φ0 равна π/3, т.е.:
A=3, ω=2 и φ0= π/3. Период колебаний T=2π/ω.

графика функции y=3 sin (2x+π/3)
Строим исходный график функции y= sin

x

Используя параллельный перенос сдвигаем график функции y= sin x
влево по оси абсцисс на расстояние π/3

Сжимаем график функции y= sin (x+π/3) в 2 раза по оси абсцисс

Растягиваем график функции y= sin (2x+π/3) в 3 раза по оси ординат