Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Хеширование
Содержание
- 1. Хеширование
- 2. Недостатки прямого создания ЦПНизкая скорость (особекнно
- 3. Для преобразования сообщения в короткую последовательность используется
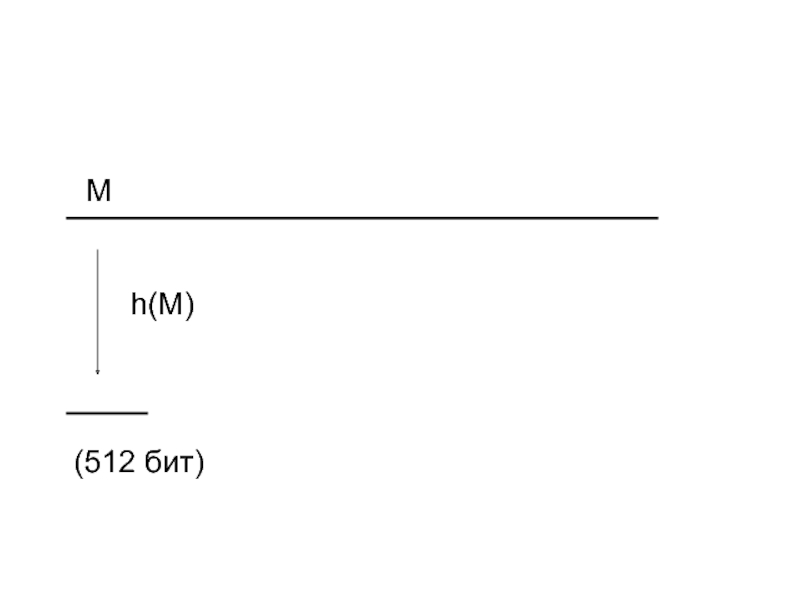
- 4. h(M)M(512 бит)
- 5. Подписывается не сообщение, а хеш от сообщения Создание Es=f(h(M),kA) Передача (M;Es) Проверка h(M)=g(Es,KA)
- 6. Чтобы исключить возможность подделки цифровой подписи, должно
- 7. Необходимость в выполнении четвертого условия связана с
- 8. Возьмем группу из m человек и событие,
- 9. Предположим, что длина хеша составляет L бит,
- 10. Слайд 10
- 11. ЦП создается для цепочки 512 бит (быстро)Размер ЦП совпадает с h(M) , т.е. 512 бит
- 12. ГОСТ Р 34.10 2001 цп(ГОСТ Р 34.11 94) хешСША DSS (DSA + SHA-256)
- 13. Скачать презентанцию
Недостатки прямого создания ЦПНизкая скорость (особекнно для больших сообщений)Подписанное сообщение имеет удвоенный объемРешение – сообщение перед подписыванием преобразуется в короткую цепочку данных
Слайды и текст этой презентации
Слайд 2Недостатки прямого создания ЦП
Низкая скорость
(особекнно для больших сообщений)
Подписанное сообщение
имеет удвоенный объем
цепочку данныхСлайд 3
Для преобразования сообщения в короткую последовательность используется так называемое хеширование
(to hash – рубить, перемалывать).
Результат хеширования h, т.е. хеш,
является хеш-функцией h = h (M) сообщения M. Он имеет фиксированную длину, не зависящую от размера аргумента, к которому применена хеш-функция.Поскольку длинных различных последовательностей больше, чем коротких, рассматриваемое преобразование не обладает свойством взаимной однозначности: одному хешу может соответствовать не один, а множество аргументов.
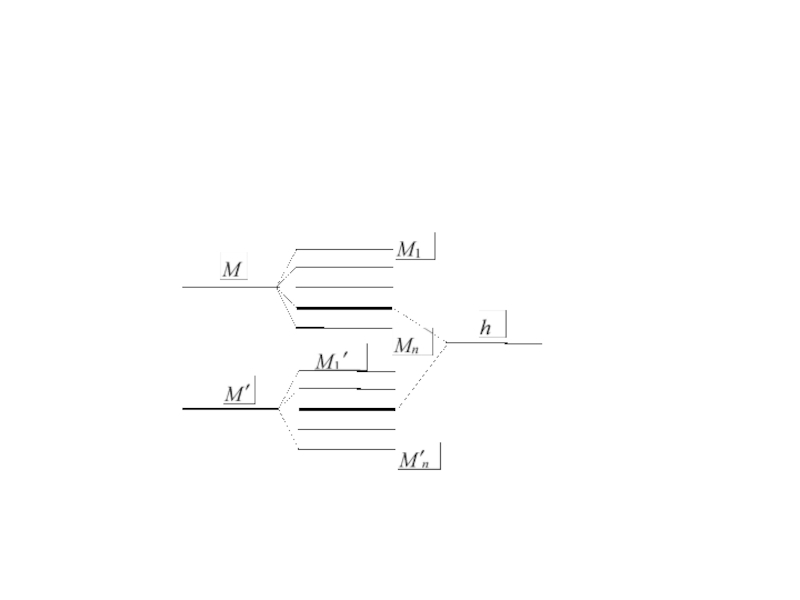
Применение простого хеширования обладает очевидным недостатком: любая пара сообщений M и M, имеющая общий хеш, дает и одинаковую цифровую подпись.
Слайд 5Подписывается не сообщение, а хеш от сообщения
Создание Es=f(h(M),kA)
Передача (M;Es)
Проверка h(M)=g(Es,KA)
Слайд 6Чтобы исключить возможность подделки цифровой подписи, должно использоваться однонаправленное хеширование,
обладающее следующими свойствами:
При известном сообщении M вычисление h = h (M) должно быть
простым, причем без использования какого-либо ключа. Это означает, что процедура хеширования может быть выполнена любым пользователем. Применяемые при этом хеш-функции называются бесключевыми (бесключевое хеширование).По известному хешу h должно быть трудно найти сообщение M такое, чтобы h = h (M), т.е. вычисление обратной функции должно быть сложным.
По заданному сообщению M должно быть трудно найти другое такое сообщение M (M M ), чтобы h (M) = h (M ).
Должно быть трудно найти любую пару таких сообщений M и M, для которых h (M ) = h (M ).
Слайд 7Необходимость в выполнении четвертого условия связана с важной атакой на
цифровую подпись, использующую хеш-функцию. Эта атака, основана на так называемом
парадоксе дней рождения.Слайд 8Возьмем группу из m человек и событие, состоящее в том,
что, по крайней мере, два человека в группе имеют один
и тот же день рождения. Оказывается, что если m 23, то вероятность такого события не меньше, чем 1/2.Более формально:
Пусть имеется n мест и m предметов, которые случайно размещаются на этих местах. Вероятность события, состоящего в том, что на любом из n мест окажется более одного предмета при равна