Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного
Содержание
- 1. Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного
- 2. Что такое интеграл?Интеграл – одно из важнейших
- 3. Определенный интегралОпределенный интеграл от функции f (x)
- 4. 1. Значение определенного интеграла не зависит от
- 5. 4. Если функция y=f(x) интегрируема на [a,b] и a
- 6. Если функция y=f(x) непрерывна на отрезке
- 7. Пример 1. вычислить интеграл Решение. Для подынтегральной
- 8. Вычисление длин дуг с помощью определенного интеграла.
- 9. Пример. Вычислить Область интегрирования – часть смещенного круга, ограниченная кривыми
- 10. Вычисление площади с помощью интеграла Криволинейная трапеция
- 11. Вычисление объема с помощью определенного интегралаЕсли тело
- 12. Спасибо за внимание!
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1«Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения
длин, площадей и объемов»
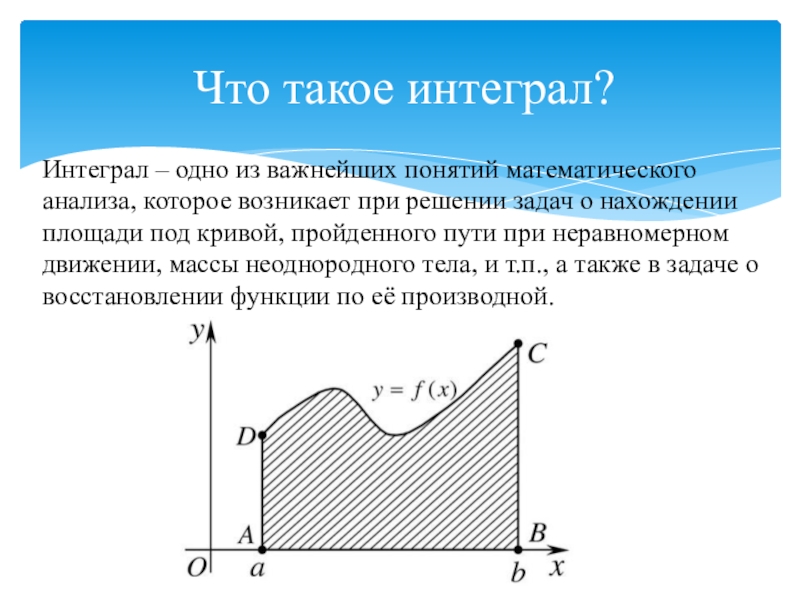
Слайд 2Что такое интеграл?
Интеграл – одно из важнейших понятий математического анализа,
которое возникает при решении задач о нахождении площади под кривой,
пройденного пути при неравномерном движении, массы неоднородного тела, и т.п., а также в задаче о восстановлении функции по её производной.Слайд 3Определенный интеграл
Определенный интеграл от функции f (x) , непрерывной на
отрезке [a,b], вычисляется по формуле:
где, F(x) – первообразная для
функции f(x), т.е. F’ (x)=f (x). Формула называется формулой Ньютона Лейбница.
Слайд 41. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
2. Постоянный множитель можно выносить за знак определенного интеграла:
Свойства
определенного интегралаСлайд 54. Если функция y=f(x) интегрируема на [a,b] и a
5. (теорема о среднем). Если функция y=f(x) непрерывна на отрезке
[a,b], то 3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
Слайд 6
Если функция y=f(x) непрерывна на отрезке [a,b] и F(x)
– какая-либо ее первообразная на этом отрезке, то справедлива следующая
формула:которая называется формулой Ньютона-Лейбница. Разность F(b) – F(a) принято записывать следующим образом:
где символ называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
(2)
Формула Ньютона - Лейбница
Слайд 7Пример 1. вычислить интеграл
Решение. Для подынтегральной функции f(x)=x2 произвольная
первообразная имеет вид
Так как в формуле Ньютона – Лейбница
можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид:Слайд 8Вычисление длин дуг с помощью определенного интеграла.
Если x=x(t), y=y(t),
t[t1,t2] – параметрические уравнения гладкой кривой, то длина ее дуги
равнагде x(t) и y(t) - производные функции x(t) и y(t) соответственно, по параметру t.
Существует аналогичная формула для длины дуги пространственной гладкой кривой.
x=x(t), y=y(t)z=z(t), t [t1,t2] :
Слайд 10Вычисление площади с помощью интеграла
Криволинейная трапеция – фигура, ограниченная
отрезком [a,b] оси Ох, отрезками прямых x=a, x=b и графиком
непрерывной на отрезке [a,b] функции y=f(x), где f(x)≥0 при x €[a,b].Слайд 11Вычисление объема с помощью определенного интеграла
Если тело заключено между двумя
перпендикулярными к оси Ox плоскостями, проходящими через точки x= a
и x=b, тоГде S(x) – площадь сечения тела плоскостью, которая проходит через точку и перпендикулярна к оси Ox.
Пример. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды y=sinx
Решение: Воспользуемся формулой для вычисления объема тела вращения получаем
далее вычисляется определенный интеграл:

![Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного Определенный интегралОпределенный интеграл от функции f (x) , непрерывной на отрезке Определенный интегралОпределенный интеграл от функции f (x) , непрерывной на отрезке [a,b], вычисляется по формуле: где, F(x)](/img/tmb/6/575311/506017340fdf1e6b6f55a3775cac45a2-800x.jpg)

![Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного 4. Если функция y=f(x) интегрируема на [a,b] и a 4. Если функция y=f(x) интегрируема на [a,b] и a](/img/tmb/6/575311/b5fdaeb7b9e9436e9145370f9d6de833-800x.jpg)
![Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке,](/img/tmb/6/575311/03dd8c827934a38fe3eac75916bd4ffe-800x.jpg)

![Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного Вычисление длин дуг с помощью определенного интеграла. Если x=x(t), y=y(t), t[t1,t2] Вычисление длин дуг с помощью определенного интеграла. Если x=x(t), y=y(t), t[t1,t2] – параметрические уравнения гладкой кривой, то](/img/tmb/6/575311/c7cf87e6c498095452338819073c73da-800x.jpg)

![Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного Вычисление площади с помощью интеграла Криволинейная трапеция – фигура, ограниченная отрезком Вычисление площади с помощью интеграла Криволинейная трапеция – фигура, ограниченная отрезком [a,b] оси Ох, отрезками прямых x=a,](/img/tmb/6/575311/097cac4462d58ee2831b5a019b5ba777-800x.jpg)





















