Слайд 1ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
НЕИЗВЕСТНЫХ ПАРАМЕТРОВ
Слайд 2ВОПРОС 45:
Интервальные оценки
Слайд 3Определение. ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ (надежностью) оценки Θ* параметра Θ называется вероятность
γ того, что выполняется неравенство
|Θ* - Θ|<δ.
Или: P ( Θ* - δ < Θ < Θ* + δ ) = γ.
Определение. ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ называется интервал, в который попадает неизвестный параметр с заданной надежностью γ.
Слайд 4ВОПРОС 46:
Доверительный интервал для оценки математического ожидания нормального распределения при
известной дисперсии
Слайд 7ВОПРОС 47:
Доверительный интервал для оценки математического ожидания нормального распределения при
неизвестной дисперсии
Слайд 11ВОПРОС 48:
Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
Слайд 12Найти (s–δ, s+δ) : P(|σ – s| < δ)
= γ
Выразим (1) через
Слайд 16ВОПРОС 49:
Общие принципы проверки гипотез. Основные определения.
Слайд 17Определение. СТАТИСТИЧЕСКОЙ ГИПОТЕЗОЙ называют гипотезу о виде неизвестного распределения генеральной
совокупности или о параметрах известных распределений.
Определение. НУЛЕВОЙ (основной) называют выдвинутую
гипотезу Н0.
АЛЬТЕРНАТИВНОЙ называют гипотезу Н1, которая противоречит нулевой.
Слайд 18Определение. Простой называют гипотезу, содержащую только одно предположение, сложной –
гипотезу, состоящую из конечного или бесконечного числа простых гипотез.
Слайд 19Возможны ошибки двух видов:
- ошибка первого рода, состоящая в
том, что будет отвергнута правильная нулевая гипотеза («пропуск цели»),
-
ошибка второго рода, заключающаяся в том, что будет принята неверная гипотеза («ложная тревога»).
Слайд 20Определение. Вероятность ошибки первого рода называется уровнем значимости α.
Определение.
Статистическим критерием называется правило со случайным показателем К и с
известным законом распределения, служащая для проверки нулевой гипотезы H0.
Слайд 21Определение. Критической областью называют область значений показателя критерия К,
при которых нулевую гипотезу H0 отвергают;
областью принятия гипотезы – область
значений критерия, при которых гипотезу H0 принимают.
Слайд 22АЛГОРИТМ ПРОВЕРКИ ГИПОТЕЗЫ:
1. выбирается статистический критерий c показателем К;
2. вычисляется
наблюдаемое значение показателя Кнабл по имеющейся выборке;
Слайд 23 если вычисленное значение Кнабл попадает в область принятия гипотезы,
то нулевая гипотеза принимается, если в критическую область – нулевая
гипотеза отвергается.
поскольку з.р. показателя К известен, определяется (по известному уровню значимости α) критическое значение kкр, разделяющее критическую область и область принятия гипотезы
Слайд 24ВИДЫ КРИТИЧЕСКИХ ОБЛАСТЕЙ:
- правостороннюю критическую область, определяемую неравенством
K > kкр ( kкр > 0);
- левостороннюю критическую область,
определяемую неравенством K < kкр ( kкр < 0);
- двустороннюю критическую область, определяемую неравенствами K < k1, K > k2 (k2 > k1).
Слайд 25Определение. Мощностью критерия называют вероятность попадания критерия в критическую область
при условии, что верна конкурирующая гипотеза.
Если обозначить вероятность ошибки второго
рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1–β.
Слайд 26ВОПРОС 50:
Критерий для проверки гипотезы о вероятности события
Слайд 27Нулевая гипотеза Н0 : р= р0.
Показатель статистического критерия
q0 =
1 – p0
Если Н1: р ≠ р0
критическая область
имеет вид
Слайд 28
Если |Uнабл| < uкр,
то гипотеза Н0
принимается;
Если |Uнабл| > uкр,
то гипотеза Н0
отвергается.
АЛГОРИТМ:
Слайд 29
Функция
Лапласа
Интеграл
вероятностей
ЗАМЕЧАНИЕ: различать:
Слайд 302) Конкурирующая гипотеза Н1: р > p0,
Если Uнабл
uкр,
то гипотеза H0 принимается;
если
Uнабл > uкр,
то гипотеза H0 отвергается.
Слайд 313) Конкурирующая гипотеза Н1: р< p0,
Если Uнабл >- uкр,
то H0 принимается.
Если |Uнабл| <- uкр,
то H0 отвергается.
Слайд 32Пример. Пусть проведено 50 независимых испытаний, и относительная частота появления
события А оказалась равной p=0,12. Проверим при уровне значимости α=0,01
нулевую гипотезу Н0: р=0,1 при конкурирующей гипотезе Н1: р>0,1.
Слайд 33ВОПРОС 51:
Критерий для проверки гипотезы о математическом ожидании
Слайд 34
Н0: E(Х) = а0.
Если |Uнабл| < uкр, то H0 принимается;
если |Uнабл|>uкр, то нулевая гипотеза отвергается
Слайд 35Н1:
Н0 принимается, если
Uнабл < uкр
Н1:
Н0 принимается, если
Uнабл < -uкр
Слайд 36Дисперсия генеральной совокупности неизвестна
Если | Tнабл | < t0,
то Н0 принимается.
Если | Tнабл | > t0, то Н0
отвергается.
Слайд 37ВОПРОС 52:
Критерий для проверки гипотезы о сравнении двух дисперсий
Слайд 38
Распределение Фишера-Снедекора со степенями свободы k1=n1–1 и k2=n2 – 1
Fкрит(α; k1; k2)
При FнаблFкр
Н0 отвергается.
NB! При Н1: D(X)≠D(Y) Fкрит(α/2; k1; k2)
Слайд 39Проверка статистических гипотез о предполагаемом законе распределения
Слайд 40ВОПРОС 53:
Критерий Пирсона для проверки гипотезы о виде закона распределения
Слайд 41Проверка гипотезы
о нормальном распределении
Наблюдения……….. х1 х2
… хs
Частоты………..…… n1 n2 … ns
,
k=s–1–r =s-3
Слайд 43Проверка гипотезы о равномерном распределении
Слайд 45Проверка гипотезы
о показательном распределении
k = s – 2
Слайд 47
- показатель критерия Колмогорова
Слайд 48Приближенное значение λn(α) вычисляется
по формуле
где z – корень
уравнения
На практике для вычисления значения
статистики Dn используется то,
что
Слайд 49Fn(x) ±λn(α)
Н0 верна, если график функции F(x) не выходит
за пределы области, лежащей между графиками функций Fn(x) -λn(α) и
Fn(x) +λn(α).
Слайд 50ВОПРОС 55:
Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов
асимметрии и эксцесса
Слайд 51Определение. Асимметрия эмпирического распределения определяется равенством
Эксцесс эмпирического распределения
определяется равенством




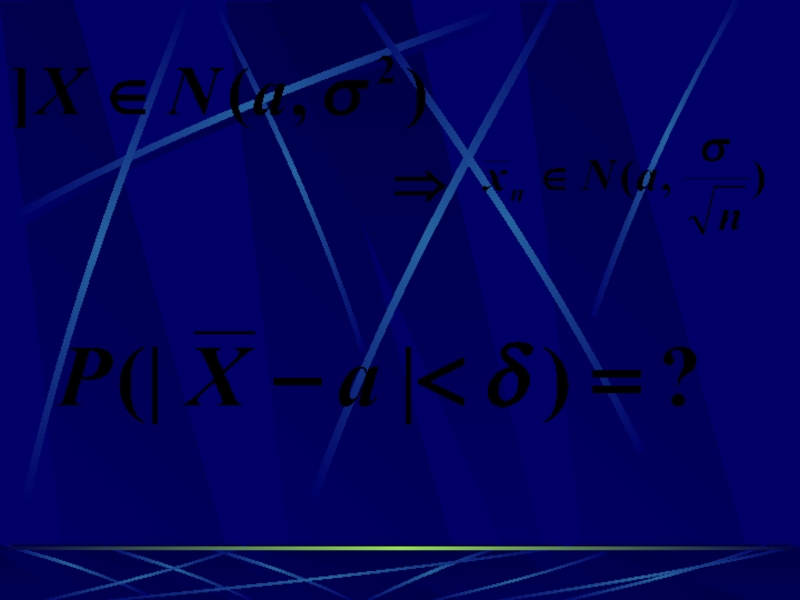




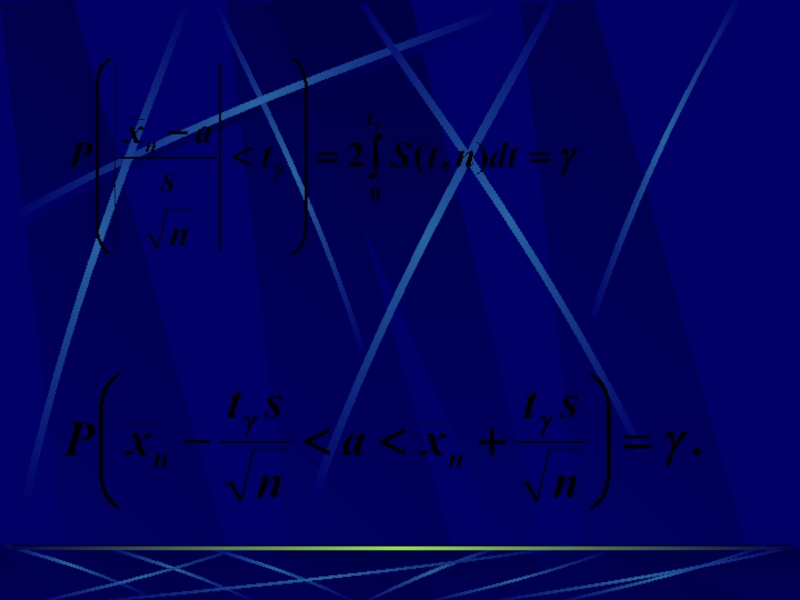


![Интервальное оценивание неизвестных параметров ] q ] q](/img/thumbs/e4696ae15e27aae9b4201f73da309a87-800x.jpg)
![Интервальное оценивание неизвестных параметров ] q>1 Замечание: ] q>1 Замечание:](/img/thumbs/85258ba3ebcb38d951de08fcf8927362-800x.jpg)