Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИСТОРИЯ систем счисления Информатика 9 класс Красноперова Е.Н
Содержание
- 1. ИСТОРИЯ систем счисления Информатика 9 класс Красноперова Е.Н
- 2. Так говорили пифагорейцы,
- 3. Числа... они с
- 4. Цифры - это символы,
- 5. Система счисления— это знаковая система, в которой
- 6. Итак, рассмотрим различные непозиционные системы счисления.Непозиционные системы счисления возникли раньше позиционных.
- 7. Непозиционной системой счисления- называется такая система счисления,
- 8. Сначала люди просто различали
- 9. Первыми понятиями математики были "меньше", "больше", "столько же". >
- 10. Достаточно было положить рядом с каждой рыбой
- 11. Счет появился тогда, когда
- 12. Имена числительные во многих
- 13. С их помощью можно было считать до
- 14. Однако известны народы, у
- 15. Например, на крупнейшей мировой бирже в Чикаго
- 16. Появилась потребность в записи
- 17. Единичная («палочная») периоду палеолита 10-11 тысяч
- 18. Чем больше зерна собирали
- 19. 2,5 тысяч лет до н.э. Древнеегипетская десятичная = 2342
- 20. Слайд 20
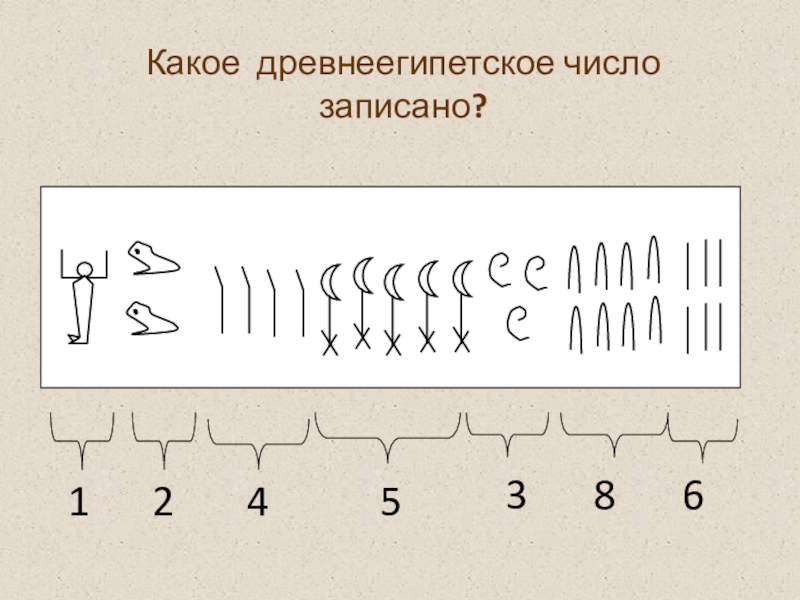
- 21. Какое древнеегипетское число записано?
- 22. Римская десятичная I , V, Х, L,
- 23. В римской системе для обозначения чисел используются
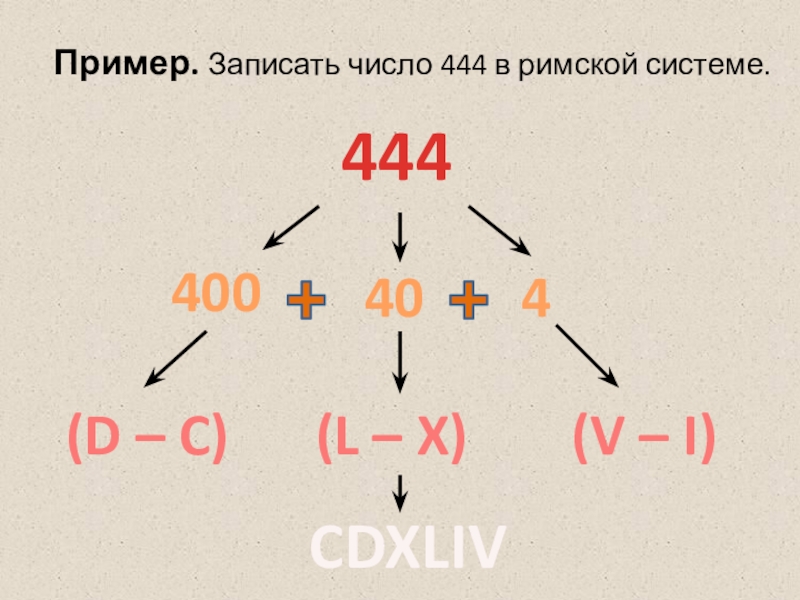
- 24. 444Пример. Записать число 444 в римской системе.(D – C)(L – X)(V – I)
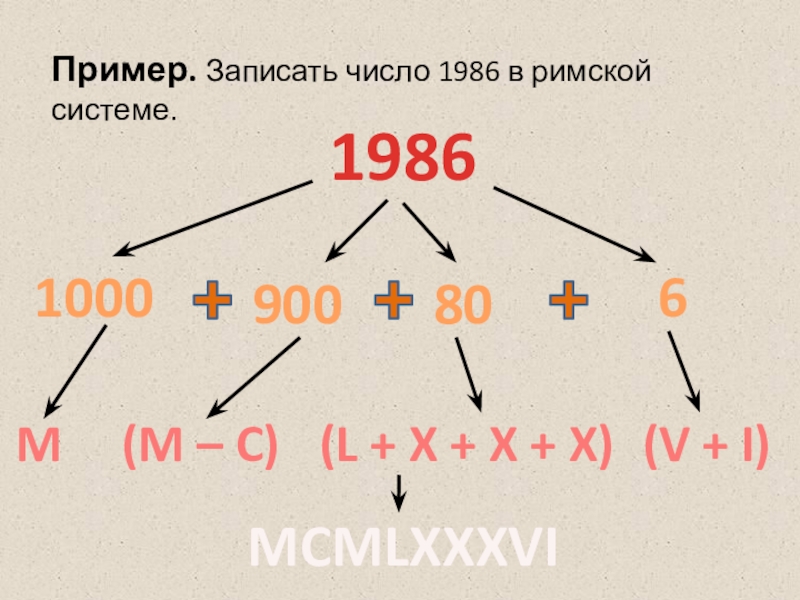
- 25. 1986Пример. Записать число 1986 в римской системе.M
- 26. Греки применяли несколько способов
- 27. В старину на Руси широко
- 28. В IX веке монахами братьями Кириллом и
- 29. Слайд 29
- 30. Мы видим, что
- 31. Эта форма записи чисел была официальной на
- 32. Непозиционной системой счисления- называется такая система счисления,
- 33. Недостатки непозиционной системы счисления1.Существует постоянная потребность введения
- 34. Далее рассмотрим позиционные системы
- 35. Позиционной системой счисления- называется такая система счисления,
- 36. Любая позиционная система счисления характеризуется своим
- 37. 2 тысячи лет до н.э. Вавилонская шестидесятеричная- единицы- десяткицифры:и
- 38. И до наших дней
- 39. 10 у привычной десятичной системы счисления
- 40. Скачать презентанцию
Так говорили пифагорейцы, подчеркивая необычайно важную роль чисел в практической деятельности. «Все есть число» Современный человек каждый день запоминает номера машин и телефонов, в
Слайды и текст этой презентации
Слайд 2 Так говорили пифагорейцы, подчеркивая необычайно важную
роль чисел в практической деятельности.
Современный человек каждый день запоминает номера машин и телефонов, в магазине подсчитывает стоимость покупок, ведет семейный бюджет ...
Слайд 3 Числа... они с нами везде и
всегда.
Но в любом случае число изображалось с помощью
одного или нескольких символов -цифр. Люди всегда считали и записывали числа, даже пять тысяч лет назад. Но записывали они их совершенно по-другому, по другим правилам.
Слайд 4 Цифры - это символы, составляющие некоторый алфавит.
Что же такое тогда число?
Число - это некоторая
величина, состоящая из цифр, сложенных по определенным правилам. На разных этапах развития человечества, у разных народов эти правила были различны и сегодня мы их называем системами счисления.
Слайд 5Система счисления
— это знаковая система, в которой все числа записываются
по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Непозиционные
Позиционные
Слайд 6Итак, рассмотрим различные непозиционные системы счисления.
Непозиционные системы
счисления возникли
раньше позиционных.
Слайд 7Непозиционной системой счисления
- называется такая система счисления, у которой количественный
эквивалент («вес») цифры не зависит от ее местоположения в записи
числа.
Слайд 8 Сначала люди просто различали ОДИН предмет перед
ними или нет.
Если предмет был не один,
то говорили«МНОГО»
" alt="Первыми понятиями математики были "меньше", "больше", "столько же". >">Слайд 10Достаточно было положить рядом с каждой рыбой по ножу, чтобы
обмен между племенами состоялся.
Если одно племя
меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. 
Слайд 11 Счет появился тогда, когда человеку потребовалось сообщать
своим соплеменникам о количестве найденных им предметов.
И, так как
многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.
Слайд 12 Имена числительные во многих языках указывают, что
у первобытного человека орудием счета были преимущественно пальцы.
Пальцы оказались прекрасной вычислительной машиной. 
Слайд 13С их помощью можно было считать до 5, а если
взять две руки, то и до 10.
30
100
Десятичная система счета
впоследствии стала общеупотребительной.
Слайд 14
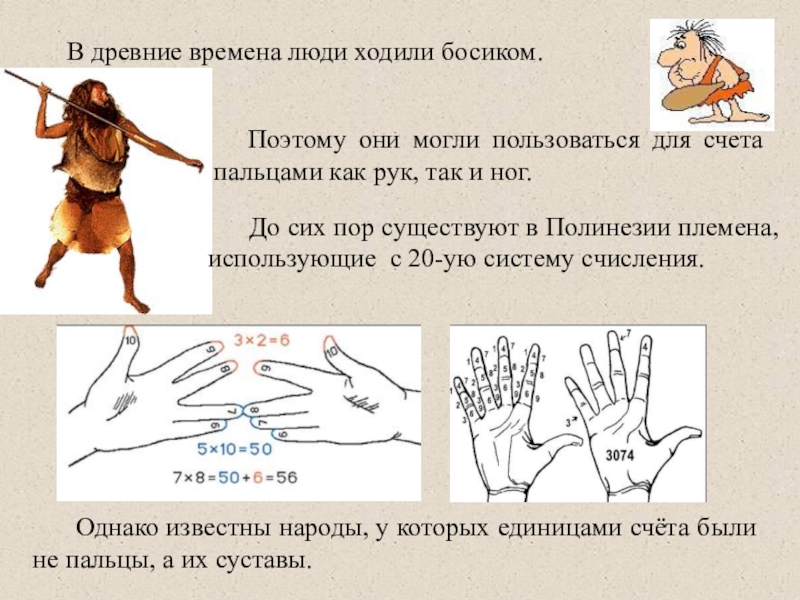
Однако известны народы, у которых единицами счёта
были не пальцы, а их суставы.
Поэтому они могли
пользоваться для счета пальцами как рук, так и ног. В древние времена люди ходили босиком.
До сих пор существуют в Полинезии племена, использующие с 20-ую систему счисления.
Слайд 15Например, на крупнейшей мировой бирже в Чикаго предложения и запросы,
как и цены объявляются маклерами на пальцах без единого слова.
Пальцевой
счет сохранился кое-где и поныне 
Слайд 16 Появилась потребность в записи чисел.
Запомнить большие числа было трудно, поэтому к «счетной машине» рук
и ног стали добавлять различные приспособления. Количество предметов изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине…
Слайд 17Единичная («палочная»)
периоду палеолита
10-11 тысяч лет до н.э.
Археологами найдены такие "записи" при раскопках культурных слоев,
относящихся к Любое число в ней образуется повторением одного знака - единицы.
Слайд 18 Чем больше зерна собирали люди со своих
полей, чем многочисленнее становились их стада, тем большие числа становились
им нужны. Единичная запись для таких чисел была громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа.
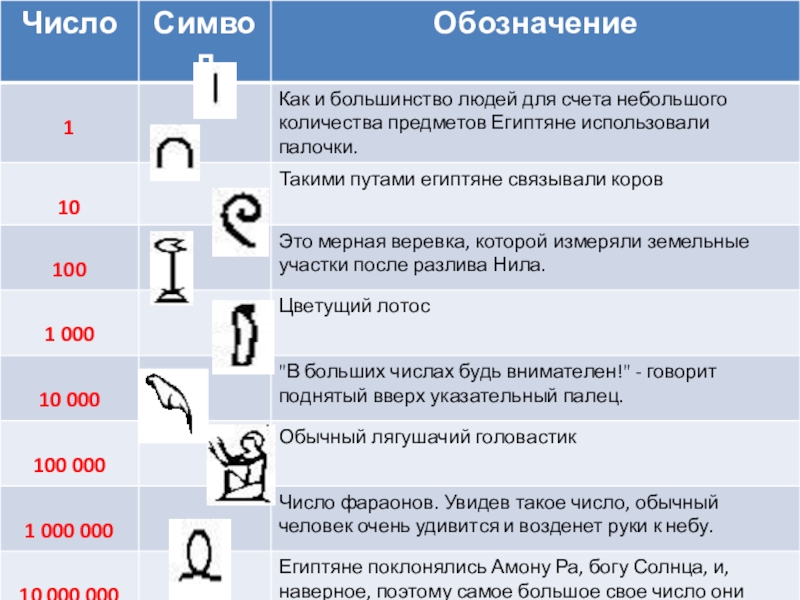
Слайд 22Римская десятичная
I , V, Х, L, C, D, M
Число в римской системе счисления обозначается набором стоящих
подряд «цифр».тысячи лет до н.э.
и до наших дней
Слайд 23В римской системе для обозначения чисел используются знаки:
I (один
палец) для числа 1,
V (раскрытая ладонь) для числа 5,
X (две сложенные ладони) для 10,
а для других чисел используются заглавные латинские буквы соответствующих латинских слов
50 - L, 100 – Сentum, 500 – Demimille, 1000 – Mille,
являющиеся «цифрами».
Слайд 26 Греки применяли несколько способов записи чисел. Афиняне
для обозначения чисел пользовались первыми буквами слов-числительных:
Греческая (ионийская)
Например,
I, II,
III, IIII - 1, 2, 3, 4IIII – 10+10+10+4 = 34
Слайд 27 В старину на Руси широко применялись системы счисления,
напоминающие систему Древнего Египта.
С их помощью сборщики податей
заполняли квитанции об уплате подати (ясака) и делали записи в податной тетради. Звезда – тысяча рублей
Колесо – сто рублей
Квадрат – десять рублей
Х - рубль
| - копейку.
Древняя Русь
1232 руб. 24 коп.
Слайд 28В IX веке монахами братьями Кириллом и Мефодием
Эта форма записи
чисел получила большое распространение в связи с тем, что имела
полное сходство с греческой записью чисел.была создана новая нумерация вместе со славянской алфавитной системой для перевода священных библейских книг.
Слайд 30 Мы видим, что запись получилась не
длиннее нашей десятичной. Это объясняется тем, что в алфавитных системах
использовалось, по крайней мере, 27 «цифр».Пример. Запишем число 444 в славянской системе.
Слайд 31Эта форма записи чисел была официальной на территории современной России,
Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии
до реформы Петра
I (до конца XVII века).Но до сих пор православные церковные книги используют эту нумерацию.
Слайд 32Непозиционной системой счисления
- называется такая система счисления, у которой количественный
эквивалент («вес») цифры не зависит от ее местоположения в записи
числа.
Слайд 33Недостатки непозиционной системы счисления
1.Существует постоянная потребность введения новых знаков для
записи больших чисел.
2.Невозможно представлять дробные и отрицательные числа.
3.Сложно выполнять арифметические
операции, так как не существует алгоритмов их выполнения. 
Слайд 34
Далее рассмотрим позиционные системы счисления.
Но мы до сих пор пользуемся элементами непозиционной системы счисления
в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Слайд 35Позиционной системой счисления
- называется такая система счисления, у которой количественный
эквивалент («вес») цифры зависит от ее местоположения в записи числа.
Рассмотрим
два числа 52 и 25. Цифры одни и те же – 5 и 2,
а чем эти числа отличаются?
Позицией цифры в числе.
Слайд 36 Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы
счисления — количество различных цифр, используемых для изображения чисел в
данной системе счисления.За основание можно принять любое натуральное число — два, три, четыре, ..., образовав новую позиционную систему: двоичную, троичную, четверичную и ...
Слайд 38 И до наших дней сохранились следы счета
шестью десятками.
Окружность делят на 3600, то есть
6*60 градусов,градус - на 60 минут,
а минуту - на 60 секунд.
До сих пор мы делим час на 60 минут, а минуту на 60 секунд.
Слайд 39 10 у привычной десятичной системы счисления (десять пальцев на
руках). Алфавит: 1, 2, 3, 4, 5, 6, 7, 8,
9, 0.60 придумано в Древнем Вавилоне: деление часа на 60 минут, минуты — на 60 секунд, угла — на 360 градусов.
12 распространили англосаксы: в году 12 месяцев, в сутках два периода по 12 часов, в футе 12 дюймов.
7 используется для счета дней недели
Основания, используемые в наши дни
