Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Изучение динамики явлений (анализ динамических, временных рядов)
Содержание
- 1. Изучение динамики явлений (анализ динамических, временных рядов)
- 2. Динамический ряд - ряд однородных величин, характеризующих изменение явления во времени.
- 3. Анализ динамических рядов :· выявление закономерности изменения изучаемого явления во времени;· прогнозирование (экстраполирование) полученных данных на последующие годы.
- 4. Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).
- 5. Типы динамических рядов: 1. В зависимости от
- 6. Типы динамических рядов: 3. В зависимости от
- 7. Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости их уровней.
- 8. Для оценки сопоставимости проводят предварительный анализ полученных
- 9. Методика анализа динамических рядов Представить полученные данные
- 10. Методика анализа динамических рядов 3. Если
- 11. Для выявления и описания тренда динамический ряд подвергают обработке - выравниванию.
- 12. Методика анализа динамических рядов Для выявления и описания тренда динамический ряд подвергают обработке - выравниванию.
- 13. Способы выравнивания динамических рядов: 1.Укрупнение временных
- 14. Аналитический способ (метод наименьших квадратов) При
- 15. Т.е. уровни ряда рассматриваются как функция времени,
- 16. Наиболее часто в качестве моделииспользуются следующие функции:
- 17. Для выравнивания ряда чаще всего выбирают линейную
- 18. Способ наименьших квадратов позволяет найти теоретическую кривую,
- 19. где у - уровни фактического ряда; n - количество уровней;t - порядковый номер временного периода.
- 20. Эта система уравнений легко упрощается, если «t»
- 21. При нечетном ряде середина обозначается через 0,
- 22. При четном ряде две средние временные точки
- 23. При отсчете времени от середины ряда Σt = 0 и система нормальных уравнений принимает вид:
- 24. Отсюда находим параметры уравнения:
- 25. Подставляя в уравнение у = а0 +
- 26. Заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.
- 27. Оценка точности аппроксимации возможна с помощью нахождения: а)
- 28. б) коэффициент расхождения Тейла:где у - фактический
- 29. После аналитического выравнивания динамического ряда и описания
- 30. Экстраполяция осуществляется путем подставления в найденное уравнение
- 31. Вычисление основных показателей динамического ряда:
- 32. Условные обозначения:yi - текущий уровень ( сравниваемый);уi-1-
- 33. 1. Абсолютный прирост ( убыль) :
- 34. 2. Темп роста (убыли):
- 35. 3. Темп прироста (убыли) (относительная скорость ) :
- 36. 4.Средний темп прироста (убыли ): где а0; а1
- 37. 5.1% прироста ( убыли ): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.
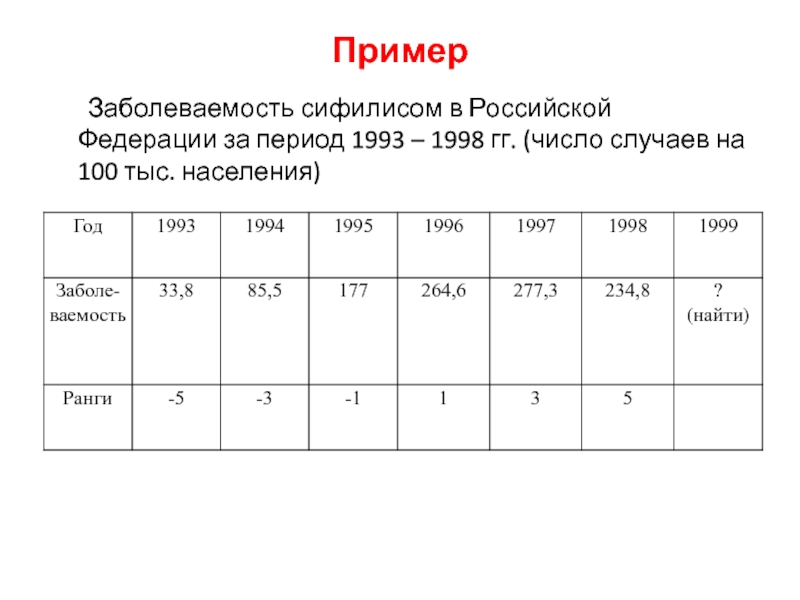
- 38. Пример Заболеваемость сифилисом в Российской Федерации за период
- 39. ПримерНа основании условия задачи необходимо;1. Выровнять динамический
- 40. В качестве модели (аппроксимирующей функции) выбираем линейную зависимость:
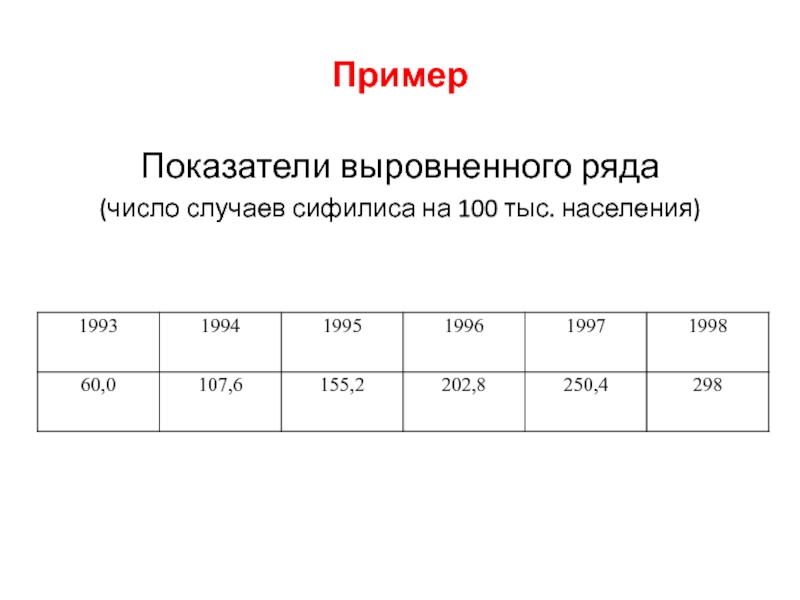
- 41. ПримерПоказатели выровненного ряда(число случаев сифилиса на 100 тыс. населения)
- 42. ПримерПоказатели динамического ряда:Абсолютный прирост Темп прироста Темп
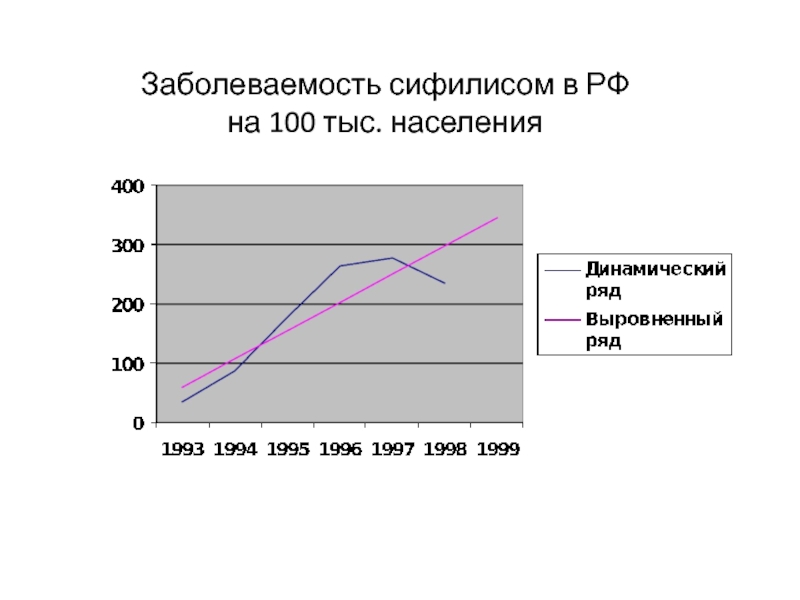
- 43. Заболеваемость сифилисом в РФ на 100 тыс. населения
- 44. Вывод: Заболеваемость сифилисом в РФ за период
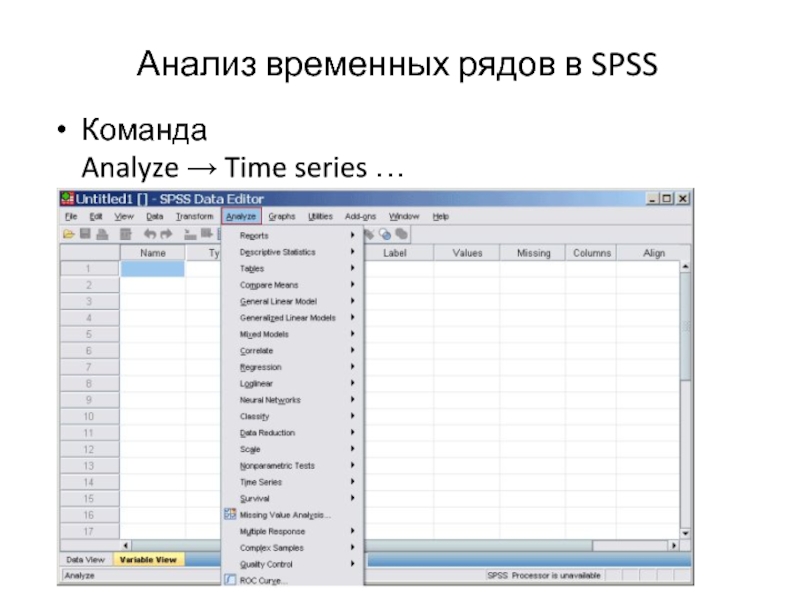
- 45. Анализ временных рядов в SPSSКоманда Analyze → Time series …
- 46. Спасибо за внимание!
- 47. Скачать презентанцию
Динамический ряд - ряд однородных величин, характеризующих изменение явления во времени.
Слайды и текст этой презентации
Слайд 3Анализ динамических рядов :
· выявление закономерности изменения изучаемого
явления во времени;
· прогнозирование (экстраполирование)
полученных данных на последующие годы.
Слайд 5Типы динамических рядов:
1. В зависимости от вида уровня ряда:
а) простые
(уровень ряда выражен абсолютными числами);
б) сложные (уровень ряда выражен обобщающими
коэффициентами).2. В зависимости от способа формирования временного интервала:
а) моментные (данные собираются на определенный момент времени);
б) интервальные (данные собираются за определенный период времени).
Слайд 6Типы динамических рядов:
3. В зависимости от выраженности изменений явления во
времени (определяется по коэффициенту корреляции между временем и изучаемым явлением).
а)
с выраженной тенденцией (r =0,7 - 1,0);б) с неустойчивой тенденцией (r =0,3 - 0,69);
в) с отсутствием тенденции ( r = 0 - 0,29).
Слайд 7Основное требование, предъявляемое к анализируемым динамическим рядам, заключается в сопоставимости
их уровней.
Слайд 8 Для оценки сопоставимости проводят предварительный анализ полученных данных по следующим
критериям:
единство территории, на которой проводился сбор данных;
единая методология учета данных;
единые
временные интервалы, в течение которых проводилась регистрация данных.Слайд 9Методика анализа динамических рядов
Представить полученные данные графически и выявить
форму зависимости изучаемого явления от времени.
2. Оценить наличие и силу
корреляции изучаемого явления от времени Слайд 10Методика анализа динамических рядов
3. Если установлено, что ряд
обладает выраженной тенденцией, проводят анализ компонентов динамики ряда:
основной тенденции
(эволюции, тренда),кратковременных систематических движений
случайных колебаний
4. Основная задача анализа - разделить эти компоненты и выявить основную закономерность изменения явления во времени
Слайд 12Методика анализа динамических рядов
Для выявления и описания тренда динамический
ряд подвергают обработке - выравниванию.
Слайд 13
Способы выравнивания динамических рядов:
1.Укрупнение временных интервалов (периодов), в течение которых
изучается явление.
2.Сглаживание ряда методом скользящей средней.
3.Аналитический способ (метод наименьших квадратов).
Слайд 14
Аналитический способ (метод наименьших квадратов)
При этом способе на основании фактических
данных подбирается наиболее подходящее для отражения тенденции развития явления математическое
уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени.Слайд 15 Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания
сводится к
определению вида функции;
отысканию ее параметров по эмпирическим
данным; расчету по найденной формуле теоретических выровненных уровней.
Слайд 16Наиболее часто в качестве модели
используются следующие функции:
а) линейная зависимость:
б)
экспоненциальная зависимость:
в) показательная зависимость:
г) параболическая зависимость:
и др.
где a0,
a1, а2 - параметры уравнения; у – теоретический уровень;
t – временной интервал.
Слайд 17Для выравнивания ряда чаще всего выбирают линейную зависимость, используя для
нахождения параметров уравнения а0 ,а1 способ наименьших квадратов.
Слайд 18Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к
эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от
фактических позволяет свести математическое решение задачи к системе нормальных уравнений:Слайд 19где
у - уровни фактического ряда;
n - количество уровней;
t -
порядковый номер временного периода.
Слайд 20Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые
номера), ведя отсчет времени от середины ряда.
Слайд 21При нечетном ряде середина обозначается через 0, а отсчет рангов
ведется через единицу с соответствующим знаком в ту или иную
сторону от середины(например: -5,-4,-3,-2,-1, 0,+1.+2,+3,+4,+5).
Слайд 22При четном ряде две средние временные точки обозначаются через +1
и -1, а остальные ранги присваиваются через две единицы (например:
-5,-3,-1,+1,+3,+5).Слайд 25Подставляя в уравнение у = а0 + а1t вместо «t»
его ранги, находим выровненные (теоретические) значения уровней ряда и строим
теоретическую кривую выровненного динамического ряда.Слайд 26Заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности
аппроксимации с определенным уровнем значимости.
Слайд 27Оценка точности аппроксимации возможна с помощью нахождения:
а) коэффициента вариации:
где у- фактический
уровень ряда;
yt - теоретический уровень ряда;
k- число параметров
уравнения; n- число уровней ряда.
Аппроксимация считается точной при Cv не более 15%.
Слайд 28б) коэффициент расхождения Тейла:
где у - фактический уровень ряда;
yt
- теоретический уровень ряда.
Аппроксимация считается точной при U не
более 5%
Слайд 29После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать
полученные данные.
Экстраполяция предполагает сохранение тренда, базирующееся на допущении неизменности
влияющих факторов и предшествующей тенденции. Слайд 30Экстраполяция осуществляется путем подставления в найденное уравнение аппроксимации не фактического
значения временного интервала, а того периода, на который прогнозируется результат.
Слайд 32 Условные обозначения:
yi - текущий уровень ( сравниваемый);
уi-1- базисный уровень (с
которым сравнивают);
t- период времени, в течение которого уровень предполагается неизменным.
Слайд 36 4.Средний темп прироста (убыли ):
где а0; а1 - параметры уравнения;
k
= 1 при нечетном ряде;
k = 2 при четном ряде.
Слайд 375.1% прироста ( убыли ): используются при сравнении динамических рядов
с уровнями, выраженными различными обобщающими коэффициентами.
Слайд 38Пример
Заболеваемость сифилисом в Российской Федерации за период 1993 – 1998
гг. (число случаев на 100 тыс. населения)
Слайд 39Пример
На основании условия задачи необходимо;
1. Выровнять динамический ряд методом наименьших
квадратов.
2. Рассчитать показатели динамического ряда (абсолютный прирост, темп роста, темп
прироста, средний темп прироста, значение 1% прироста).3. Изобразить ряд графически.
4. Дать прогноз изучаемого показателя на 1999 год.
5. Провести анализ и сделать выводы.
Слайд 42Пример
Показатели динамического ряда:
Абсолютный прирост
Темп прироста
Темп роста
Средний темп
прироста
1% роста
Прогноз на 1999 год: y = 345,6 (на 100
тыс.населения)
Слайд 44
Вывод: Заболеваемость сифилисом в РФ за период 1993-1999 г.г. имеет
выраженную тенденцию к росту (абсолютный прирост- 47,6; темп прироста- 26,5%
; темп роста – 179,3%; средний темп прироста – 26,5% ; 1% роста - 1,79).Прогноз на 1999 год: y = 345,6 (на 100 тыс.населения)