Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кафедра Вычислительных машин систем и сетей
Содержание
- 1. Кафедра Вычислительных машин систем и сетей
- 2. «Высокоточные компьютерные арифметики» (д.т.н., Оцоков Ш.А)Машинное обучение
- 3. Компьютерная арифметика
- 4. «возможность представления чисел в заданном диапазонеоднозначность представленияпростоту
- 5. Экономичная система счисления
- 6. Слайд 6
- 7. Сетунь – первый в мире троичный компьютер
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Особенности формата с плавающей точкойРезкая потеря точности
- 17. Нарушение законов алгебры
- 18. Недостатки формата с плавающей точкойЧисла с плавающей
- 19. Пример нарушения алгебраического свойства ассоциативностисложение чисел с плавающей точкой
- 20. Неравномерное распределение чисел с плавающей точкой(Длина мантиссы
- 21. ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯОбращение
- 22. Слайд 22
- 23. 8080, 8 разр, 2 МГц8086, 16 разр,
- 24. Интервальная арифметикаPascal XSC
- 25. Традиционный подход повышения точности вычисленийПрименение библиотек высокоточных
- 26. Подход к решению проблемы высокоточных вычислений на
- 27. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 28. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 29. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 30. Модулярная арифметика с дробями
- 31. Вычисления с дробями Фарея в модулярной арифметике.
- 32. Пример 1 задачи, чувствительной к изменению шага
- 33. Пример 2 задачи, чувствительной к изменению шага интегрированияПростейшее дифференциальное уравнение Число обусловленности:
- 34. ПРИМЕНЕНИЕ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ В
- 35. Оценка эффективности высокоточных вычислений на примере нахождения
- 36. МОДЕЛЬ ВЫЧИСЛЕНИЙ В МОДУЛЯРНОЙ АРИФМЕТИКИ
- 37. МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА
- 38. ИСХОДНЫЕ ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДЕЛИ Поле p-адических чисел
- 39. МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА
- 40. МОДЕЛЬ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ
- 41. ПРИМЕР ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ В
- 42. ОЦЕНКА ЭФФЕКТИВНОСТИ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ, РЕАЛИЗОВАННЫХ В MAPLE MapleКоды ГензеляСредний коэфф.абс. ускорения:Kабс 1,5
- 43. СХЕМА ОРГАНИЗАЦИИ ВЫЧИСЛЕНИЙ С ЗАДАННОЙ ТОЧНОСТЬЮ
- 44. Пусть имеются два приближения
- 45. Пусть даны x,y,z и
- 46. После выполнения операции умножения
- 47. ВОЗМОЖНЫЕ ПРИЛОЖЕНИЯ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ1.
- 48. Задачи корректныеЗадачи некорректныеЗадачи промежуточныемежду корректными и некорректнымиПлохо обусловленные задачиКлассы задачВычислительно неустойчивые алгоритмыВычисленияс исключениемошибок округления
- 49. Ф.С. ЗайцевМатематическое моделирование эволюции тороидальной плазмы. Семашко Н.Н Кафедра физики и ядерного синтеза (МЭИ)Динамическая устойчивость энергосистем...
- 50. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Кафедра Вычислительных машин систем и сетей
Московский энергетический институт
КУРС ПРОБЛЕМЫ ОРГАНИЗАЦИИ
ВЫЧИСЛЕНИЙ
Лекция на тему :
«Высокоточные вычисления»
Слайд 2«Высокоточные компьютерные арифметики» (д.т.н., Оцоков Ш.А)
Машинное обучение (д.т.н., проф. Дзегеленок
И.И., д.т.н., Оцоков Ш.А)
Геометрическое моделирования (к.т.н., Орлов Д.А.)
Технология виртуальной реальности
(к.т.н., Харитонов В.Ю)Паблик в соц сети: http://vk.com/club50059448
Направления по курсу ПОВ
Слайд 4«возможность представления чисел в заданном диапазоне
однозначность представления
простоту записи
удобство работы человека
с машиной
трудоёмкость выполнения арифметических операций
экономичность системы (количество элементов, необходимых для
представления многоразрядных чисел)удобство аппаратной реализации
Требования к системам счисления
Слайд 16Особенности формата с плавающей точкой
Резкая потеря точности при вычислениях с
разномасштабными величинами
Неравномерное распределение чисел
с плавающей точкой
Формат с плавающей
точкой
Нарушение законов алгебры (коммутативности, дистрибутивности и др.)
x ≠ (х+х)-х
…
Значения математических эквивалентных выражений могут быть не равными друг другу (вычислительные аномалии)
…
последствия
…
3
Слайд 18Недостатки формата с плавающей точкой
Числа с плавающей точки дают различные
результаты на различных аппаратных платформах.
Сложность использования численных методов (требуются экспертные
знания в области Error Analyze)Резкий рост времени вычислений при увеличении точности
В формате с плавающей точкой скрыты ошибки переполнения, исчезновения порядка ( на флаги процессора никто не смотрит)
Пример ошибки при сложении чисел в формате с плавающей точкой:
Слайд 20Неравномерное распределение чисел с плавающей точкой
(Длина мантиссы k= 3,
порядок от 0 до 4.)
Истинный результат
= 8779Вычисленный в формате с плав. точкой один. точн. равен 4.6E+0020.
Пример.
Слайд 21ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯ
Обращение матрицы Гильберта порядка
3
С точностью 2 знака после запятой
С точностью 3 знака
после запятой Макс. относ. погрешн. более 100%.
Макс. относ. погрешность более 100%.
Матрица Гильберта
Точный результат:
Слайд 238080, 8 разр, 2 МГц
8086, 16 разр, 4-10 МГц
Pentium, 32
разр, 60-233 МГц
Рост разрядности и тактовой частоты процессоров по годам
Гипотеза:
Технологические трудности создания процессоров высокой разрядностиСлайд 25Традиционный подход повышения точности вычислений
Применение библиотек высокоточных вычислений,
таких как:
ZREAL(Россия), MPARITH(Германия), GMP(США)
и др.
Основная проблема
Резкое увеличение времени
выполнения арифметических операций от точности. Это приводит к резкому
росту времени решения задач большой размерности.
Слайд 26Подход к решению проблемы высокоточных вычислений на основе модулярной арифметики
К настоящему времени модулярная арифметика
использовалась как средство повышения быстродействия в криптографии, нейронных сетях, цифровой обработке сигналов и др.Проведенные исследования показали качественно новые возможности применения модулярной арифметики в повышении точности вычислений и ослаблении зависимости времени вычислений от точности, для некоторых частных задач:
решение дифференциальных уравнений методами Рунге-Кутта,
нахождение скалярного произведения векторов,
решения систем линейных уравнений методами Гаусса-Зейделя,
релаксации,
дискретном преобразовании Фурье .
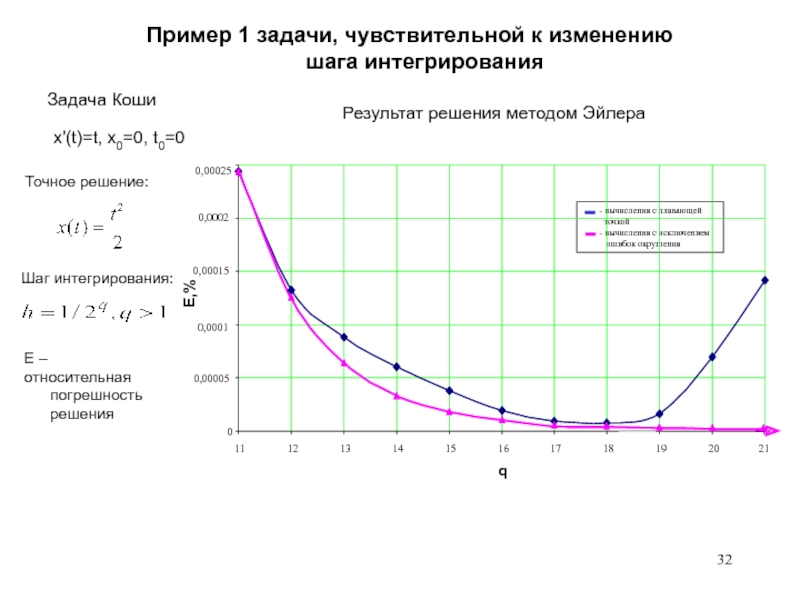
Слайд 32Пример 1 задачи, чувствительной к изменению шага интегрирования
Задача Коши
x'(t)=t, x0=0,
t0=0
Шаг интегрирования:
E – относительная
погрешность
решенияРезультат решения методом Эйлера
0
0,00005
0,0001
0,00015
0,0002
0,00025
11
12
13
14
15
16
17
18
19
20
21
q
E,%
Точное решение:
Слайд 33Пример 2 задачи, чувствительной к изменению шага интегрирования
Простейшее дифференциальное уравнение
Число обусловленности:
Слайд 34ПРИМЕНЕНИЕ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ В ВЫЧИСЛИТЕЛЬНО НЕУСТОЙЧИВЫХ АЛГОРИТМАХ
Рассмотрим
задачу вычисления функции ex . Известно, что эта задача хорошо
обусловлена.при x<0
Пример.
Найти значение функции ex при x= -15.
Верное значение e-15 =1 / e15 0.000000305902
1. Традиционные вычисления
После выполнения 82 итераций было получено: e-15 0.000000256502
Относительная погрешность
составила 19,2%.
2. Вычисления с исключ. ошибок окр.
После выполнения 60 итераций было
получено:
e-15
1822987410130384149007132206840681602541990778449289
59593604795584246682595675324534356863378751133750157901824
или e-15 0.000000305903159. Отн. погр. равна 0,0001%
Слайд 35Оценка эффективности высокоточных вычислений на примере нахождения скалярного произведения
-
время вычислений с использованием библиотеки MPArith,
- время вычислений в
модулярной арифметике при той же точности.
Слайд 37МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА ОСНОВЕ МНОГОМОДУЛЬНОЙ МОДУЛЯРНОЙ
АРИФМЕТИКИ
ось целых чисел Z
Преобраз. в многомодульную модулярную систему
Дробь
Фарея
Многомод.
модулярная
арифметика mod m1 mod mn
ось рациональных чисел Q
...
...
Обрат.
преобр
Порядок дробей Фарея
Слайд 38ИСХОДНЫЕ ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДЕЛИ
Поле p-адических чисел определяется как пополнение
множества рациональных чисел по р-адической метрике, которая является неархимедовой и
для нее выполняется неравенство «равнобедренного треугольника»Любое рациональное число имеет единственное р-адическое разложение:
Код Гензеля H(p,r,) - отрезок длины r бесконечного р-адического разложения числа .
Теорема
где m=p r
Слайд 39МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ НА ОСНОВЕ ОДНОМОДУЛЬНЫХ КОДОВ
ГЕНЗЕЛЯ
множество
p-адических чисел
Преобразование
в коды Гензеля (Hensel code)
Дробь
Фарея
Арифметика Обратн.
кодов преобр
Гензеля
Условие псевдопере-
полнения
ось рациональных чисел
Код Гензеля - конечно-разрядное р-адическое число для которого
выполняется неравенство:
, где порядок дроби
Фарея, простое число,
количество цифр в коде, дробь.
Операции сложения, вычитания,
умножения и деление выполняются
“слева направо”.
Цифры кода Гензеля в обратном
порядке образуют ичное
представление дроби по модулю
Слайд 40МОДЕЛЬ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК
ОКРУГЛЕНИЯ НА ОСНОВЕ МНОГОМОДУЛЬНЫХ
КОДОВ ГЕНЗЕЛЯ
множество
p-адических чисел
Преобразование
в многомодул. коды Гензеля с
модулями и порядкамисоответственно.
Дробь
Фарея
Параллельная
арифметика
кодов Гензеля
Условие псевдопере-
полнения
ось рациональных чисел
...
...
Обратн.
преобр.
...
...
Слайд 41ПРИМЕР ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ В
МНОГОМОДУЛЬНОЙ СИСТЕМЕ ГЕНЗЕЛЯ
Сложность арифметических операций в кодах Гензеля в двоичной системе счисления:
Коды
Гензеля могут применяться:Для реализации вычислений с полиномами (полиномиальная арифметика)
Для реализации вычислений с плавающей точкой без ошибок округления.
Слайд 42ОЦЕНКА ЭФФЕКТИВНОСТИ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ
ОШИБОК ОКРУГЛЕНИЯ, РЕАЛИЗОВАННЫХ В MAPLE
Maple
Коды Гензеля
Средний коэфф.
абс. ускорения:
Kабс 1,5
Слайд 44 Пусть имеются два приближения
к двум величинам и
- соответствующие абсолютные ошибки.Пусть количество значащих цифр в любом действительном числе, тогда при использовании правила отбрасывания максимальная относительная ошибка округления выразится так:
При симметричном округлении максимальная относительная погрешности выразится так:
Формулы относительных ошибок при 4-х арифметических операциях имеют вид:
где ошибка округления.
ФОРМУЛЫ ОТНОСИТЕЛЬНЫХ ОШИБОК ОКРУГЛЕНИЯ
Слайд 45 Пусть даны x,y,z и необходимо вычислить u=(x+y)*z
Граф вычислительного процесса имеет следующий вид:
ВЫДЕЛЕНИЕ ГРАФ-СХЕМЫ ВЫЧИСЛИТЕЛЬНОГО
ПРОЦЕССА Его следует читать
снизу вверх, следуя стрелкам.
Предположим, что три исходные величины имеют относительные ошибки округления, равные соответственно
Рассмотрим сложение. Относит. ошибка величины x составляет эта ошибка войдет в результат следующей операции (сложения) умноженной на коэффициент у стрелки, соединяющей x в кружке со знаком + в кружке:
+1
+1
Слайд 46
После выполнения операции умножения появляется ошибка
. Полная ошибка результата операции умножения выразится следующим образом:
Если
все результаты соответствующим образом округлены, то ни одна из ошибок округления не превзойдет Поэтому
АНАЛИЗ РАСПРОСТРАНЕНИЯ ОШИБОК ОКРУГЛЕНИЯ
оба неотрицательные, то
Не может быть больше 1, и окончательно имеем:
Слайд 47ВОЗМОЖНЫЕ ПРИЛОЖЕНИЯ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯ
1. Точное вычисление обобщенных
обратных матриц. Например, таких как, g-обратная матрица Мура-Пенроуза. Многие
алгоритмы требуют умения распознавать значение численного ранга, а это является трудной задачей при наличии ошибок округления.2. Целочисленное решение систем линейных уравнений. Примером могут служить построение оптимальных решений в задачах целочисленного программирования.
3. Точное вычисление характеристического многочлена матрицы. Вследствие ошибок округления будут получены приближенные значения коэффициентов. Если многочлен плохо обусловлен, то корни "приближенного» характеристического уравнения могут быть плохими приближениями к корням истинного уравнения.
4. Обращение матриц Гильберта, Адамара и др. особо чувствительных к ошибкам округления.
5. Для решения промежуточных между классами корректных и некорректных задач.
Класс задач, изменяющих корректность при решении. Это расчет устойчивости систем управления, выч. собств. знач. систем лин. одн. урав. и др.