КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ Капиллярными называются явления, связанные с искривлением

так как плоская граница (в отсутствие внешних сил) не может

существовать. Их можно наблюдать в сосудах, где сказывается кривизна поверхности, то есть когда расстояние между стенками соизмеримо с радиусом кривизны образующегося мениска жидкости.

Капиллярное давление

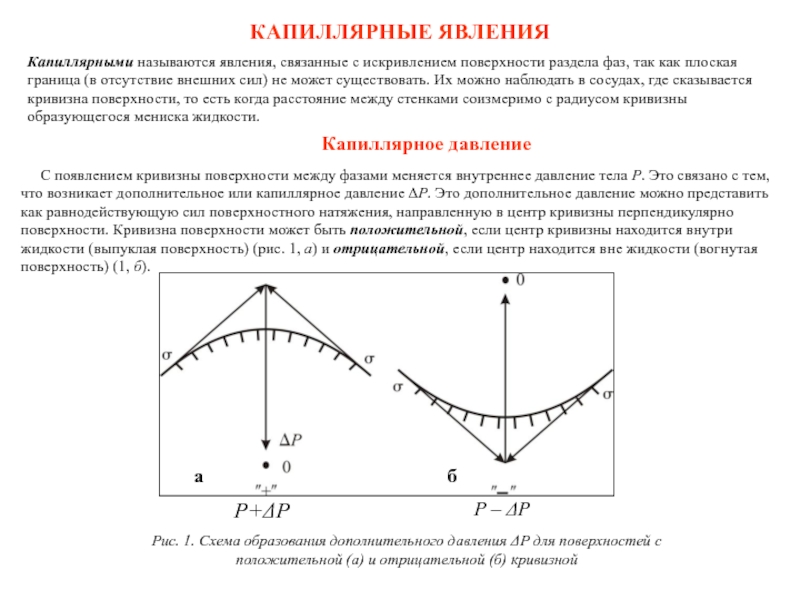
С появлением кривизны поверхности между фазами меняется внутреннее давление тела Р. Это связано с тем, что возникает дополнительное или капиллярное давление ∆Р. Это дополнительное давление можно представить как равнодействующую сил поверхностного натяжения, направленную в центр кривизны перпендикулярно поверхности. Кривизна поверхности может быть положительной, если центр кривизны находится внутри жидкости (выпуклая поверхность) (рис. 1, а) и отрицательной, если центр находится вне жидкости (вогнутая поверхность) (1, б).

Рис. 1. Схема образования дополнительного давления Р для поверхностей с положительной (а) и отрицательной (б) кривизной

а

б

P+ΔP

P – ΔP

давление жидкости, а при отрицательной – уменьшает. В первом случае

∆Р стремится сжать поверхность, а во втором – ее растянуть.
Изменение объема жидкости в обоих случаях происходит в результате самопроизвольного уменьшения поверхностной энергии и превращения ее в механическую энергию изменения объема тела δAV = ∆РdV. Процесс превращения поверхностной энергии в механическую можно описать с помощью объединенного уравнения I и II начал термодинамики. Запишем это уравнение относительно изменения энергии Гельмгольца F:

При постоянных T, n, q имеем

В состоянии равновесия:

dF = 0

где Р = ∆Р – дополнительное давление, равное разности между давлением тела с плоской и изогнутой поверхностями; dS/dV – кривизна поверхности

Для сферической поверхности

(1)

(2)

(3)

(4)

Для цилиндрической поверхности

(5)

В случае сферической поверхности получаем:
Уравнение (6) называется уравнением Лапласа, являющимся

основой теории капиллярных явлений, в котором r – радиус кривизны; 1 / r – кривизна. Для поверхности неправильной формы используют представление о средней кривизне и уравнение Лапласа имеет вид:

(6)

(7)

На законе Лапласа основан один из самых распространенных методов определения поверхностного натяжения – метод наибольшего давления пузырьков, предложенный П. А. Ребиндером. В методе измеряется давление, при котором происходит проскок газового пузырька из капилляра, опущенного в исследуемую жидкость и стандартную.

Метод наибольшего давления пузырьков (метод П.А. Ребиндера):

и для исследуемой жидкости:

разделим (9) на (8):

(8)

(9)

(10)

Запишем уравнение Лапласа
для воды по уравнению (6)

– расчетная формула
метода Ребиндера

причем чем уже капилляр, тем высота этого поднятия больше. Так,

в капиллярах почвы с r = 10-4 см; h = 15 м; r = 10-5 см, h = 150 м; r = 10-7 см,
h = 15 км.

Рис. 2. Капиллярное поднятие жидкости в капилляре при смачивании (а) – положительное капиллярное поднятие;
и несмачивании (б) – отрицательное капиллярное поднятие.

а)

б)

Рис. 3. Связь высоты капиллярного
поднятия h с параметрами капилляра и жидкости

(11)

Уравнение (11) – формула Жюрена, где ρ', ρ''  плотности жидкости и воздуха; σ  поверхностное натяжение жидкости; θ  краевой угол смачивания; R – радиус основания капилляра; r – радиус кривизны.

положительное капиллярное поднятие (h > 0)

смачивания cos θ = 1, и пренебрегая ρ''  плотностью

воздуха по сравнению с ρ'  плотностью жидкости, получаем упрощенную формулу Жюрена:

(12)

Для поднятия воды в стекле применимо уравнение (12), так как θ = 0–5°, а cos θ = 1.
Капиллярное давление будет наблюдаться и между погруженными параллельными пластинками (рис. 4). Здесь мениск имеет цилиндрическую форму, для него давление Лапласа будет в два раза меньше:

(13)

(14)

Метод определения поверхностного натяжения (по высоте капиллярного поднятия)

Уравнение 12 для исследуемой жидкости

Поделив (16) на (15), имеем расчетное уравнение метода капиллярного поднятия:

(15)

(16)

(17)

Уравнение 12 для стандартной жидкости

раздробленность вещества D, является самостоятельным термодинамическим параметром состояния системы.
С =

K – Ф + 3

где С – число степеней свободы; K – число компонентов; Ф – число фаз; 3 – число, включающее в себя, кроме переменных внешних параметров (давления и температуры) еще и дисперсность.

Дисперсность является одним из основных технологических параметров веществ и материалов во многих производственных процессах.

При выборе аппаратов в химической технологии обязательно учитываются дисперсионные характеристики системы, так как меняя дисперсность в системе, можно повлиять на растворимость вещества, на возможность переходить из одной фазы в другую, на температуру фазовых переходов, на способность вступать в химическую реакцию. Иными словами, дисперсность может повлиять на реакционную способность веществ.

В термодинамике, как известно, реакционная способность определяется энергией Гиббса ΔG. Связь между энергией Гиббса и дисперсностью в изотермических условиях можно получить с учетом уравнения Лапласа в следующем виде:

где V – объем системы; ΔP – изменение давления.

(1)

(2)

– давление насыщенного пара над искривленной поверхностью;
PS

– давление насыщенного пара над плоской поверхностью.

Сопоставляя уравнения (2) и (3), получаем:

(3)

(4)

Рис.1. Иллюстрация различия в давлениях насыщенного пара над ровной PS и вогнутыми Р1 и Р2 поверхностями

Рис. 2. Иллюстрация различия в давлениях насыщенного пара над ровной PS и выпуклыми Р1 и Р2 поверхностями

- Уравнение Томсона-Кельвина

S

x – растворимость в крупном состоянии.
Аналогично процессу испарения, имеем:
(6)
(5)
3.

Температуры фазовых переходов

(7)

где Т = Т – ТD; Hф.п – теплота фазового перехода; Т  температура плавления недиспергированного вещества; ТD  температура плавления диспергированного вещества.

Полученные из диспергированных веществ материалы обладают повышенными структурно-механическими и прочностными свойствами.

равновесия реакции, когда компоненты находятся в дисперсном состоянии;

K – константа равновесия для реагирующих веществ с невысокой дисперсностью.