Кинематика вращательного движения

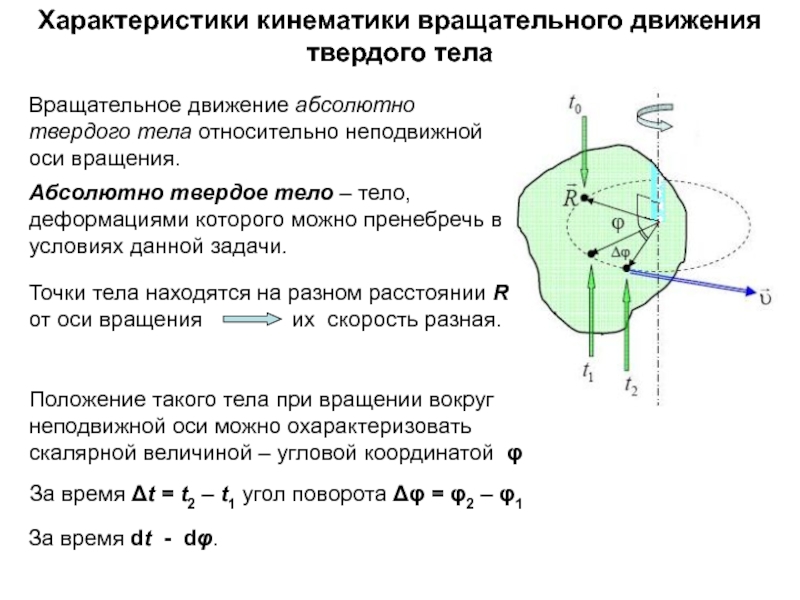
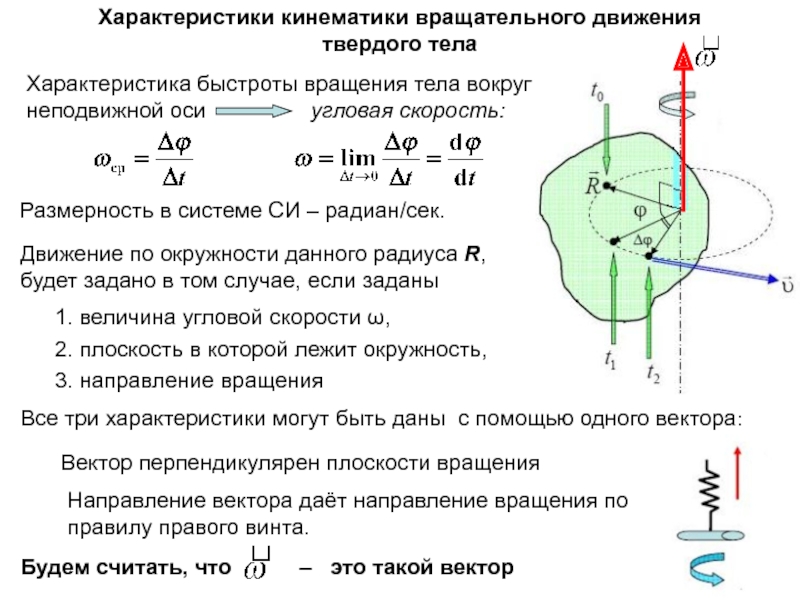
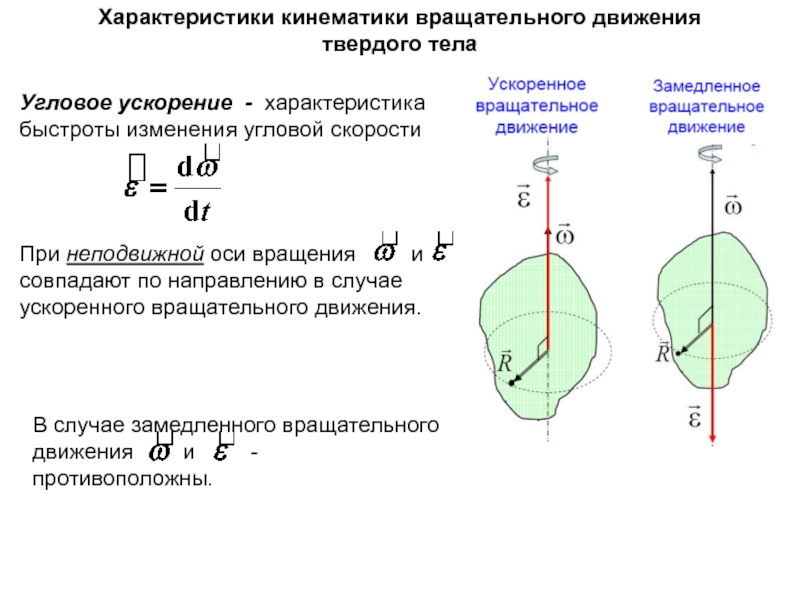
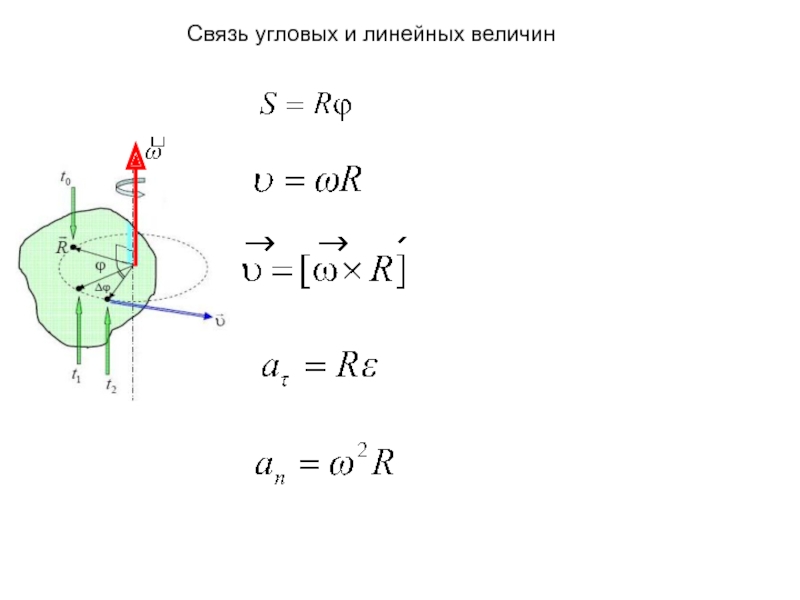
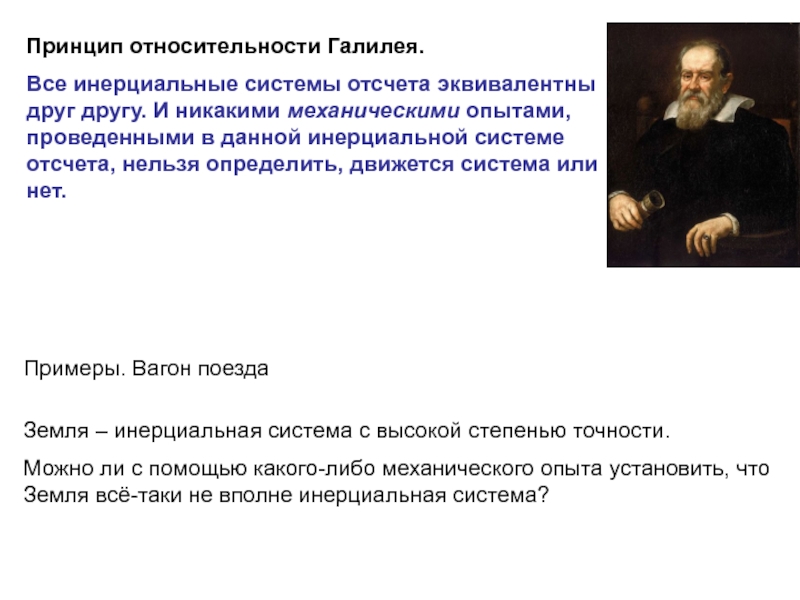
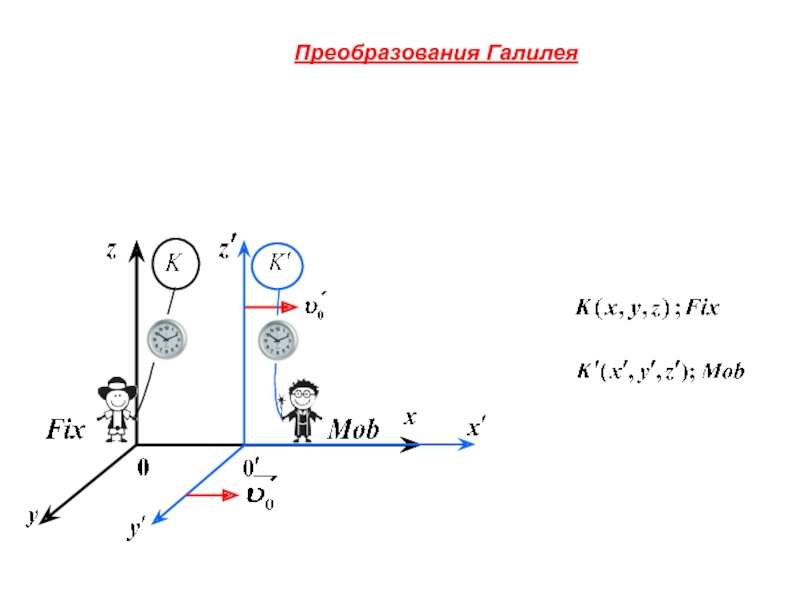
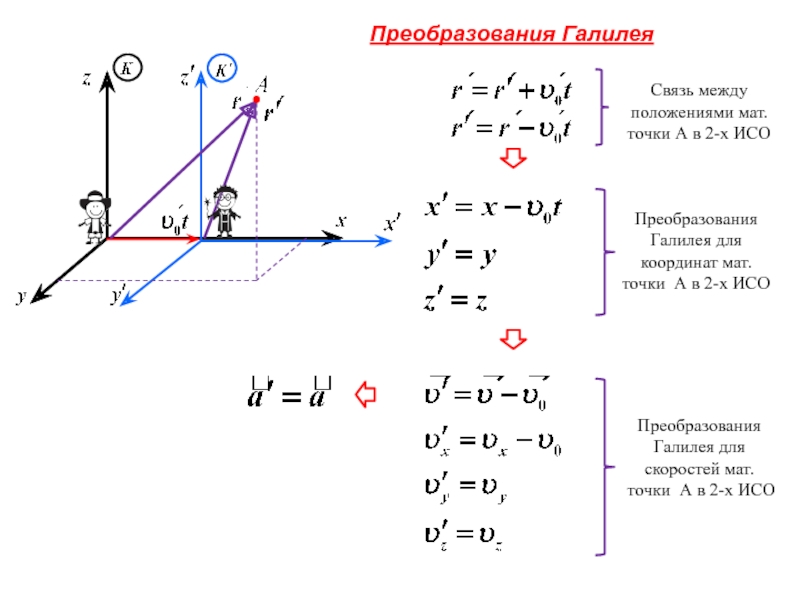
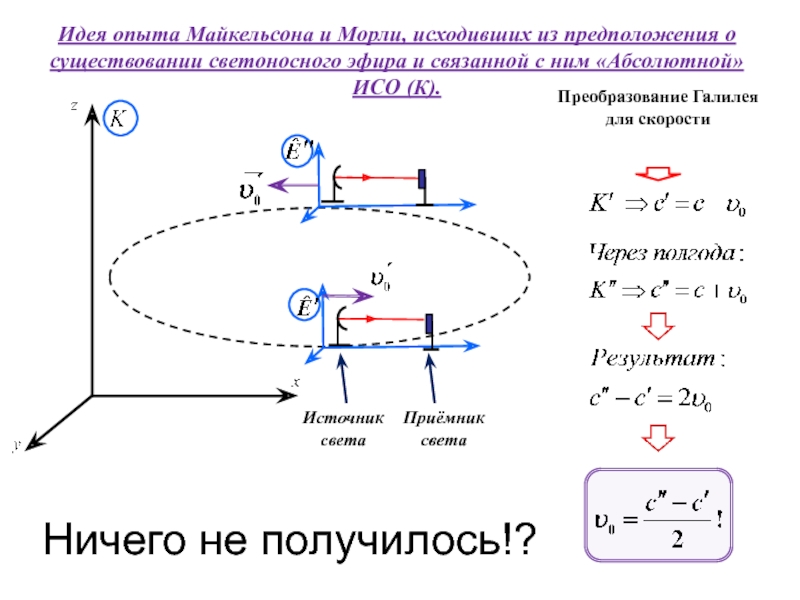
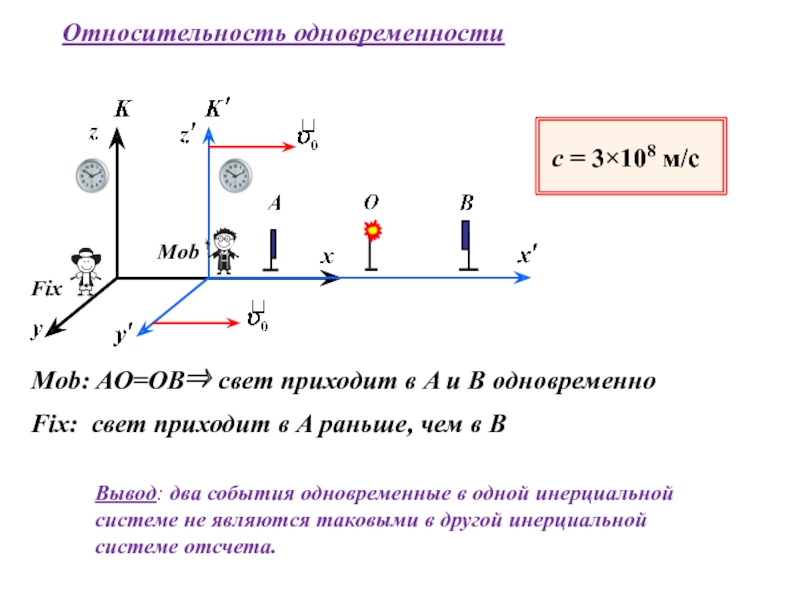
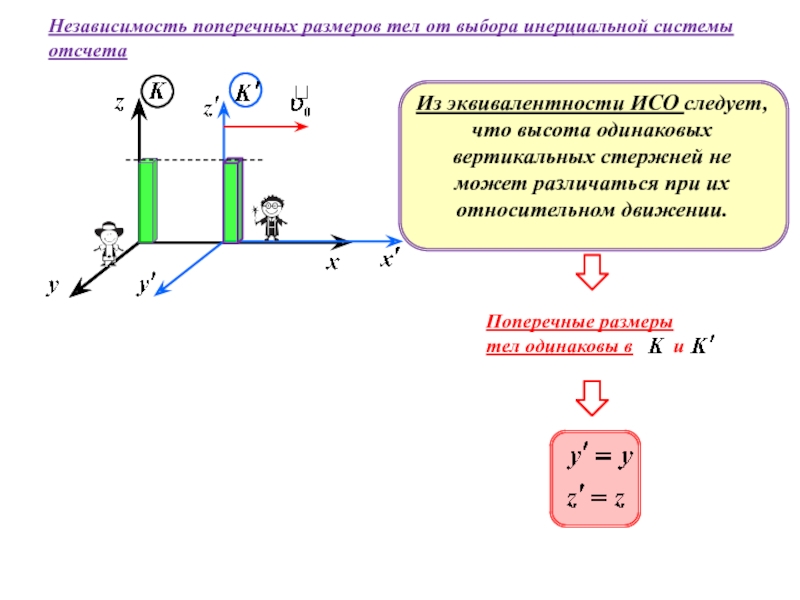
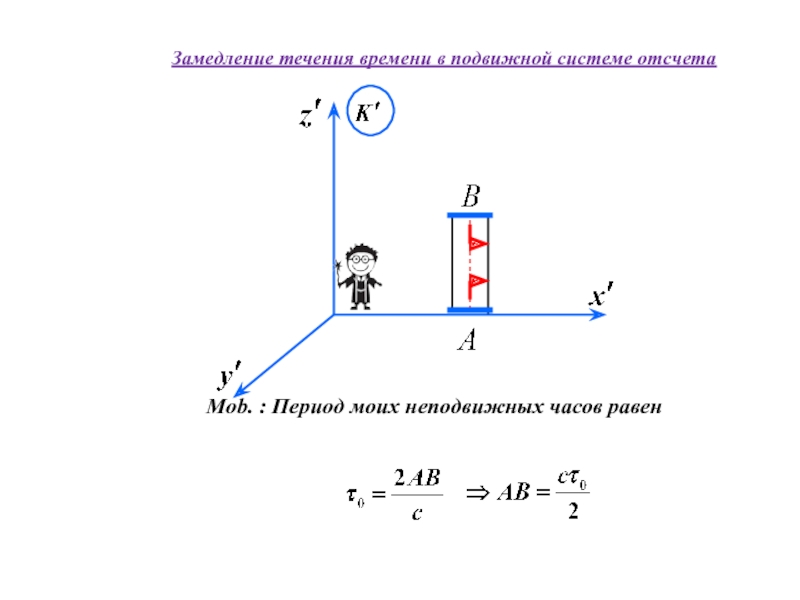
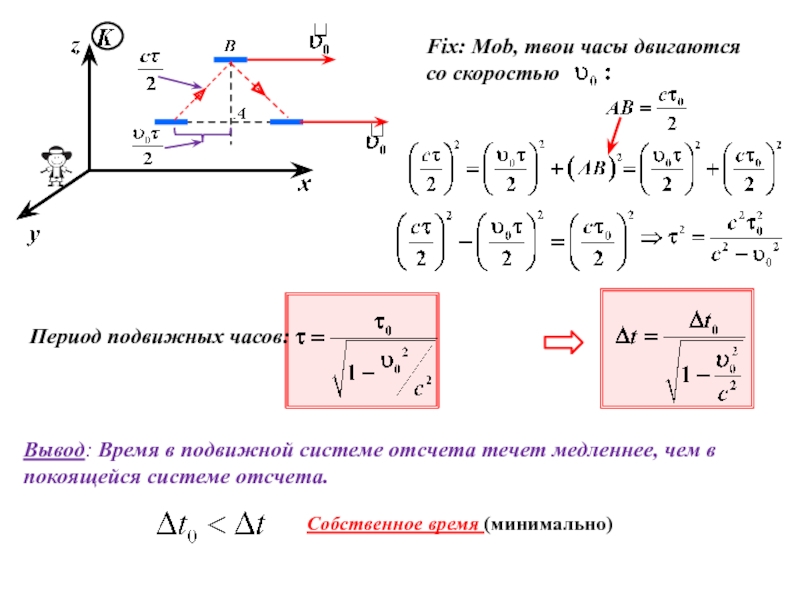
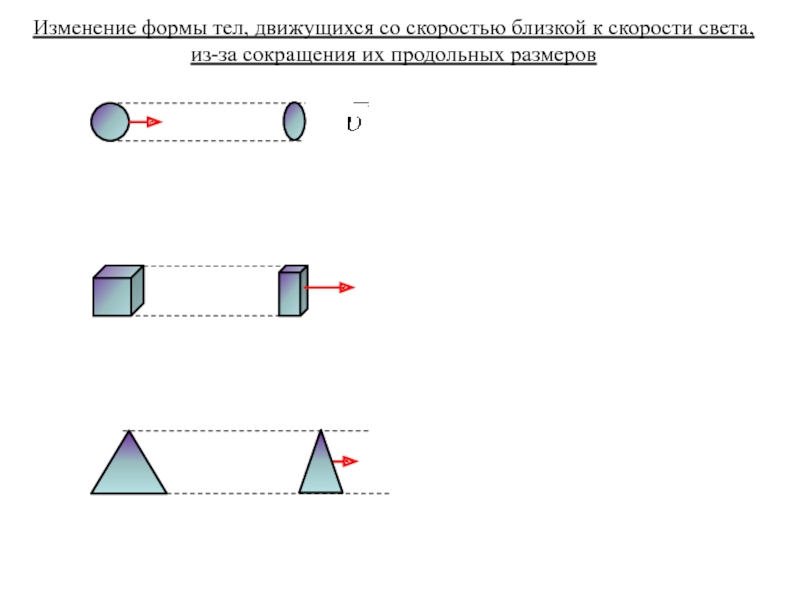
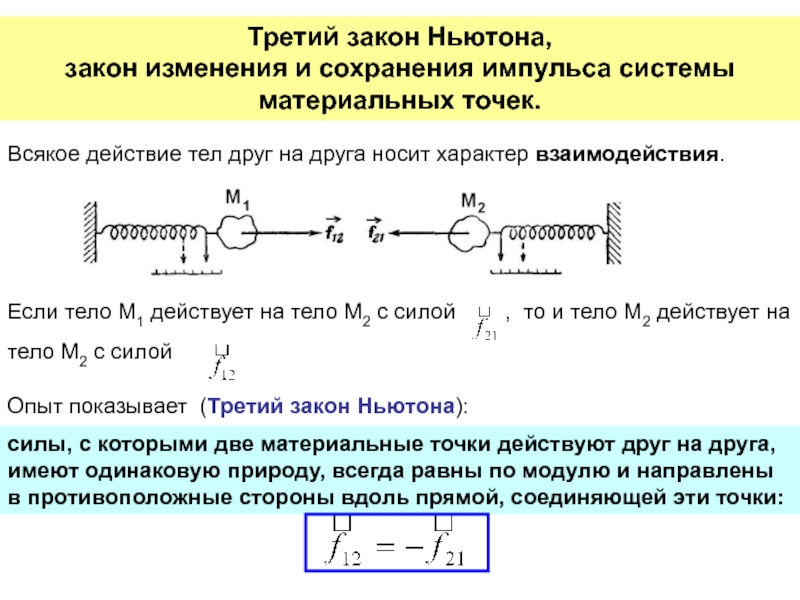
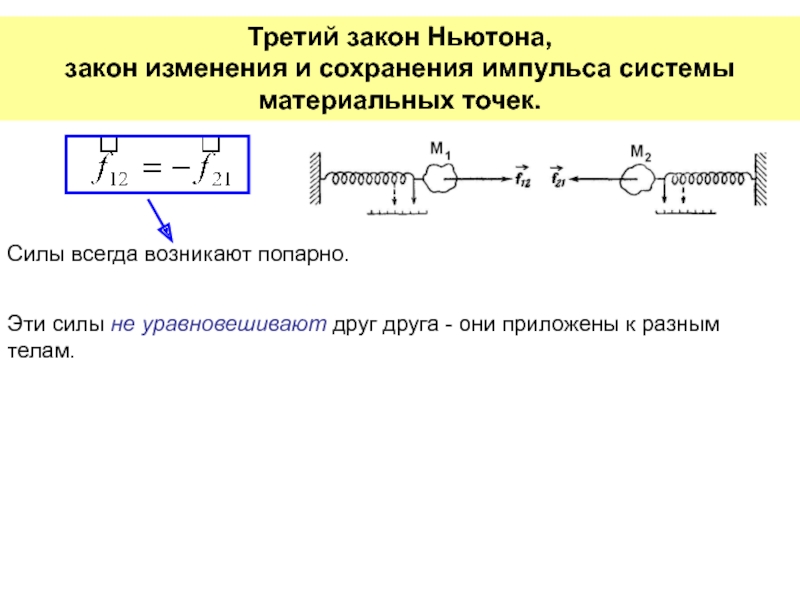
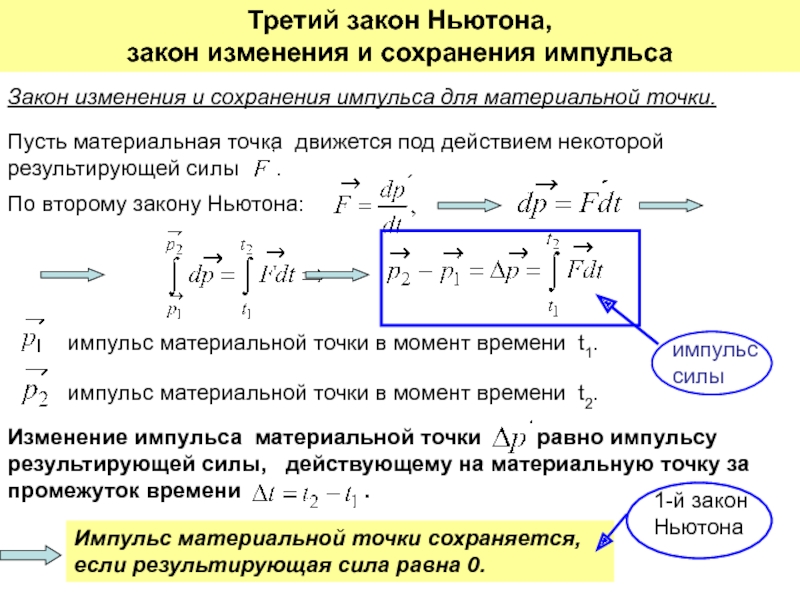
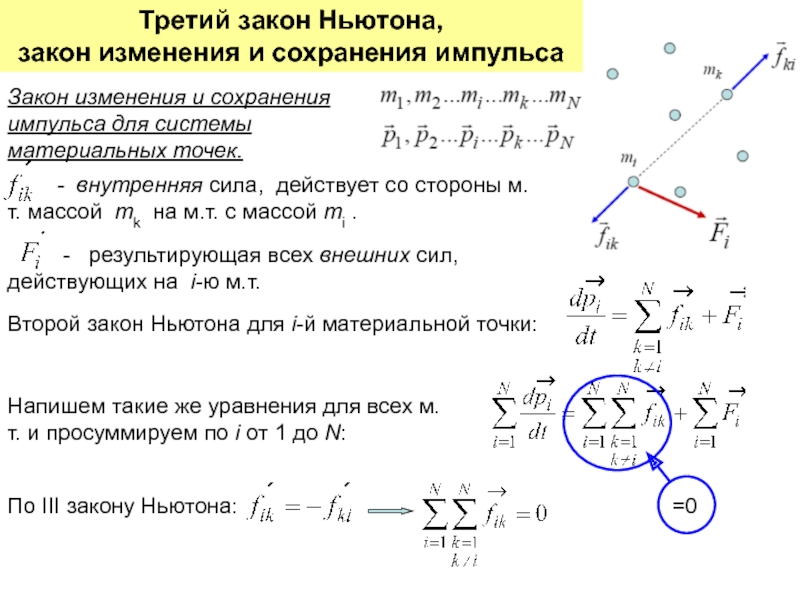
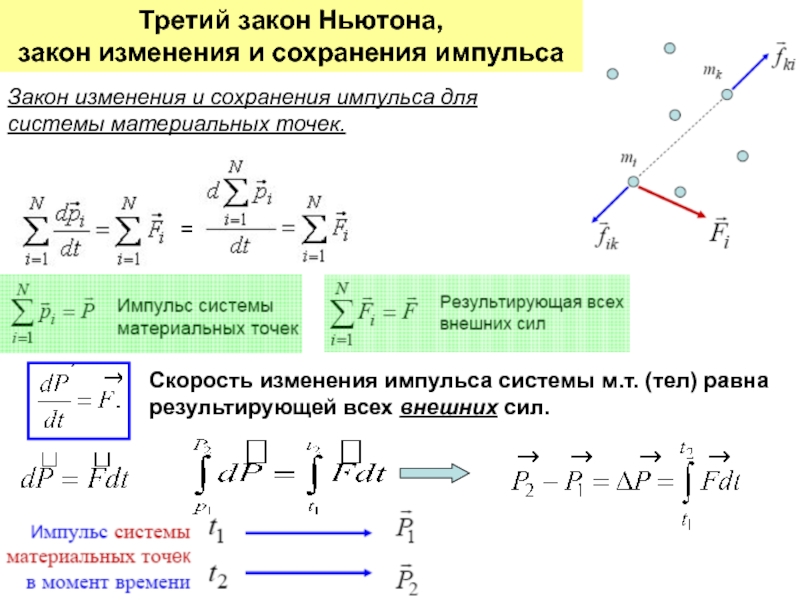
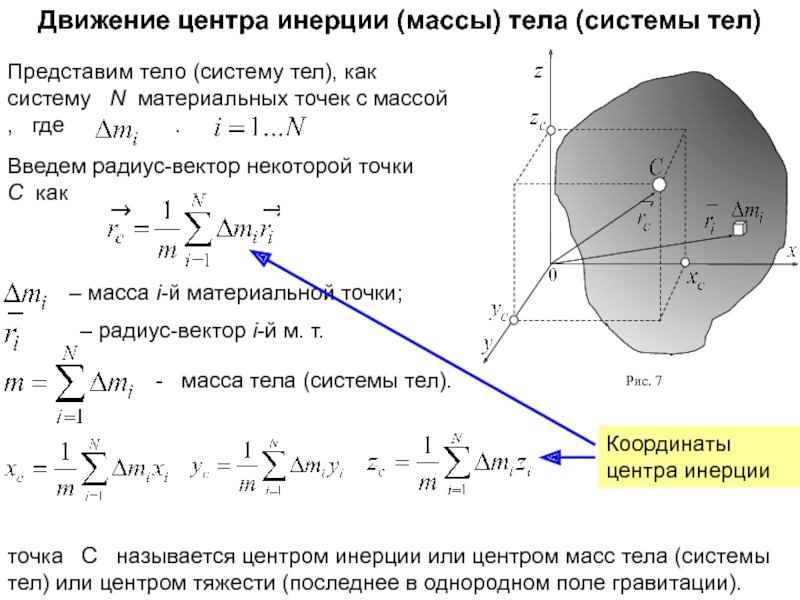
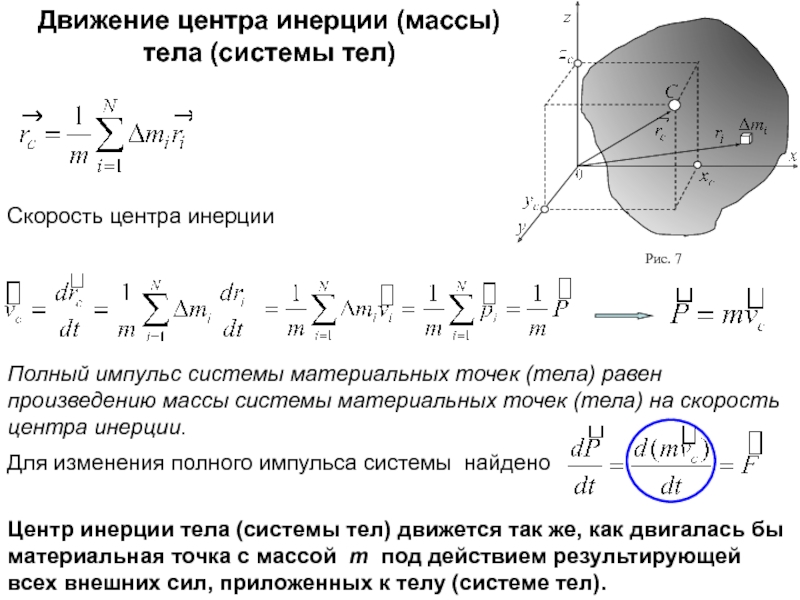
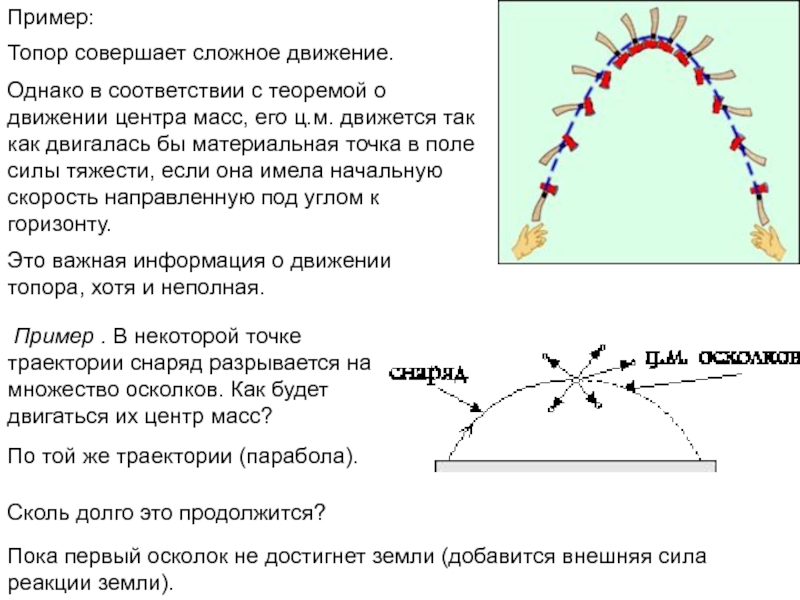
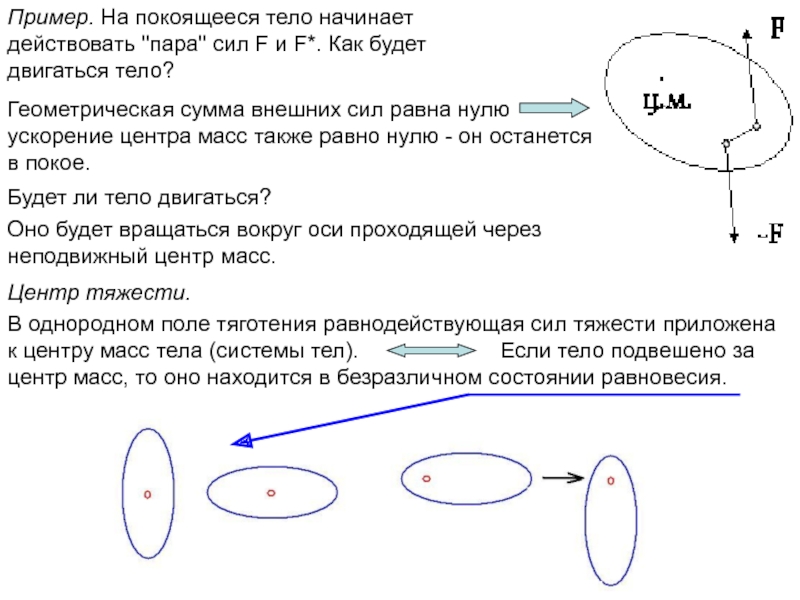
неподвижной оси вращения.
Абсолютно твердое тело – тело, деформациями которого можно

Положение такого тела при вращении вокруг неподвижной оси можно охарактеризовать скалярной величиной – угловой координатой φ

За время Δt = t2 – t1 угол поворота Δφ = φ2 – φ1

За время dt - dφ.

Движение по окружности данного радиуса R, будет задано в том

1. величина угловой скорости ω,

2. плоскость в которой лежит окружность,

3. направление вращения

Вектор перпендикулярен плоскости вращения

величина обратная периоду – число оборотов в единицу времени:
Т –

движения
твердого тела

линейной скорости точки тела и угловой скоростью:

Связь между модулями тангенциального ускорения точки тела и углового ускорения:

.

Связь между модулем нормального ускорения точки тела и модулем угловой скорости:

Связь угловых и линейных величин

.
Связь между линейной

количества опытных фактов.
Практически силы бывают скомпенсированы.
Пример: на катящийся вагон

“Движущееся тело останавливается, если сила, его толкающая, прекращает свое действие” - Аристотель

Тело движется равномерно и прямолинейно или сохраняет состояние покоя, пока воздействие других тел не изменит это состояние (закон инерции)

или сохраняет состояние покоя, пока воздействие других тел не изменит

ли с помощью какого-либо механического опыта установить, что Земля всё-таки

света в данной ИСО позволит определить её скорость относительно абсолютной

светоносного эфира и связанной с ним «Абсолютной» ИСО (К).
Ничего

с"=с'=с = 3108 м/с

от движения источника или наблюдателя и одинакова во всех направлениях,

с = 3108 м/с

– предельная скорость.

таковыми в другой инерциальной системе отсчета.
Mob
Fix
Mob: AO=OB свет приходит в

Fix: свет приходит в A раньше, чем в B

с = 3108 м/с

неподвижных часов равен

(собственное время), образующиеся в верхних слоях атмосферы (20-30 км) достигают

С т. з. наблюдателя на земле: их время течет медленнее.

С т. з. мюонов: расстояние до земли сокращается.

законы физики.

из-за сокращения их продольных размеров

и ускорение.
Сила даёт меру и направление воздействия, оказываемого на

Масса отвечает за то как тело «отзывается» на данное воздействие , т.е. за его инертность.

Сила вызывает
изменение скорости тела и его деформацию.

Прибор для измерения силы – динамометр.

Силу можно измерить и благодаря этому сравнивать силы разной природы, например, гравитационные, электромагнитные и др.

как при непосредственном контакте, так и через посредство создаваемых телами

С учётом современных представлений об атомном строении тел, силы возникающие «при непосредственном контакте» также имеют полевую природу.

свойства материи.
m ~ (число протонов + число

Тела состоят из атомов, которые в свою очередь состоят из протонов, нейтронов и электронов.

Чем больше в теле материи (протонов и нейтронов), тем оно сильнее притягивает другие тела в соответствии с законом всемирного тяготения

Чем больше в теле материи (протонов и нейтронов), тем труднее изменить его скорость в соответствии со вторым законом Ньютона:

проявлениях массы:

масс, можно второй закон применить к любому телу или системе

Второй закон относится к движению материальной точки.

Однако реально он может применяться гораздо шире благодаря теореме о движении центра масс механической системы:
центр масс движется как точка, масса которой равна массе всей системы, к которой приложены все внешние силы.

изменения импульса материальной точки во времени равна результирующей силе, действующей

Второй закон Ньютона в таком виде справедлив в частности тогда, когда классическая физика уже не корректна – при скоростях сравнимых со скоростью света, когда масса зависит от скорости.

измерения
Размерности в левой и правой части уравнения -

длина L, м,

масса M, кг,

время Т, сек.

Все другие механические величины производятся из М, L и T с помощью соответствующих уравнений.

а= Δv/Δt → [a]=LT-2 ,

точек.
Всякое действие тел друг на друга носит характер взаимодействия.

Опыт показывает (Третий закон Ньютона):

точек.

Эти силы не уравновешивают друг друга - они приложены

и сохранения импульса для материальной точки.

и сохранения импульса для системы материальных точек.

всех внешних сил, действующих на систему, равна нулю.
Пример: реактивное

закон Ньютона,
закон изменения и сохранения импульса
Закон сохранения импульса в

Закон сохранения импульса в замкнутой системе можно вывести из однородности пространства, не прибегая к 3 закону Ньютона.

Тогда 3 закон Ньютона получится как следствие закона сохранения импульса или следствие однородности пространства.

C как
точка С называется центром инерции или центром

системы материальных точек (тела) равен произведению массы системы материальных точек

Для изменения полного импульса системы найдено

Центр инерции тела (системы тел) движется так же, как двигалась бы материальная точка с массой m под действием результирующей всех внешних сил, приложенных к телу (системе тел).

множество осколков. Как будет двигаться их центр масс?
По той же

Сколь долго это продолжится?

Пока первый осколок не достигнет земли (добавится внешняя сила реакции земли).

Однако в соответствии с теоремой о движении центра масс, его ц.м. движется так как двигалась бы материальная точка в поле силы тяжести, если она имела начальную скорость направленную под углом к горизонту.

Это важная информация о движении топора, хотя и неполная.

неподвижный центр масс.
Центр тяжести.