Слайд 1Классическая электродинамика.
Введение в классическую электродинамику.
Дополнительные главы физики.
Николай Николаевич Рόзанов
февраль-июнь 2016
Слайд 2ВВЕДЕНИЕ
Теория электромагнитного поля как раздел курса «Физические основы квантовой электроники».
Основное внимание - электромагнитным волнам и их оптическому диапазону. Связь
теории электромагнитного поля с другими разделами физики. Оптические среды.
Роль электромагнитных волн. Сравнение с акустическими и другими волнами (теория волн). Фотоны – элементарные частицы (а не квазичастицы, как фононы). Эфир и вакуум.
Линейные и нелинейные волны.
Слайд 3Уравнения Максвелла в сплошной среде
Слайд 4Уравнения Максвелла, интегральная форма
S – двумерная поверхность, замкнутая для теоремы
Гаусса и открытая для законов Фарадея и Ампера (ее границей
является замкнутый контур). – электрический заряд внутри объема V, ограниченного поверхностью S.
– электрический ток, протекающий через поверхность S.
Слайд 5Справочные формулы
В декартовых координатах
В цилиндрических координатах
Слайд 6Справочные формулы
В сферических координатах
Слайд 7Материальные уравнения
Соотношения между D, B, E и H
В вакууме D
= E, B = H
В среде материальные уравнения могут иметь
вид нелокальных по времени и пространству и нелинейных соотношений (будут приведены позже).
Слайд 8Упражнения (векторный анализ)
Слайд 9Упражнения
Вывести из уравнений Максвелла закон Кулона для точечного заряда в
вакууме. Проверить выполнение всех уравнений Максвелла.
Найти напряженность эл. поля шара
с равномерной плотностью заряда.
Найти напряженность эл. поля кольцевого слоя с равномерной плотностью заряда. - дом. задание
Найти распределение плотности заряда, если известно распределение напряженности эл. поля
где А и n – постоянные,
Пояснить физический смысл результата при n = -3.
Слайд 10Уравнение непрерывности
Закон сохранения электрического заряда
Слайд 11«Площади» э.-м. поля
Рассматриваем ограниченные в пространстве и времени пакеты поля
(с конечной энергией)
Интегрируем по времени в бесконечных пределах
– «площадь» электрич.
поля – безвихревой вектор
Интегрируем по пространству (объему) в бесконечных пределах
– «площадь» магнитного поля – сохраняется
Эти общие (для любого вида материальных уравнений) соотношения полезны для контроля точности моделирования динамики поля.
Слайд 12Уравнения Максвелла в вакууме (СГС)
D = E, B = H,
ρ = 0, j = 0
Условия применимости:
Инерциальная система отсчета
Гравитационные
эффекты
Квантовые ограничения для слабых и сильных полей
Учебное пособие: Н.Н. Розанов. Специальные разделы мат. физики. Ч.I. Электромагнитные волны в вакууме. 2005.
Слайд 13Квантовые ограничения в слабых полях
Уравнения Максвелла отвечают континуальному (а не
дискретному)
описанию. Поэтому для их справедливости число фотонов в основных модах
N должно быть велико: N >> 1. Этот фактор важен при анализе шумов излучения и сжатых состояний электромагнитного поля (квантовая оптика).
Слайд 14Квантовые ограничения в сильных полях
В уравнениях Максвелла не учитываются вероятность
рождения электрон-позитронных пар и эффекты
поляризации вакуума. Необходимое условие пренебрежения этими
эффектами:
(изменение энергии заряда |e| в поле напряженности E на расстоянии равном комптоновской длине волны электрона RC = h /(mc) = 2.4 10^(-10) см должно быть много меньше mc^2 , m – масса электрона, h – постоянная Планка, ħ = h / 2π ). В мощных лазерных установках достигаются напряженности полей, близкие к критическим. Последовательная теория дается квантовой электродинамикой.
Приближенно электромагнитное поле в электрон-позитронном вакууме описывается уравнениями электродинамики сплошных сред. Комптоновская длина волны электрона описывает его «размазанность», при меньших расстояниях классическая теория неприменима.
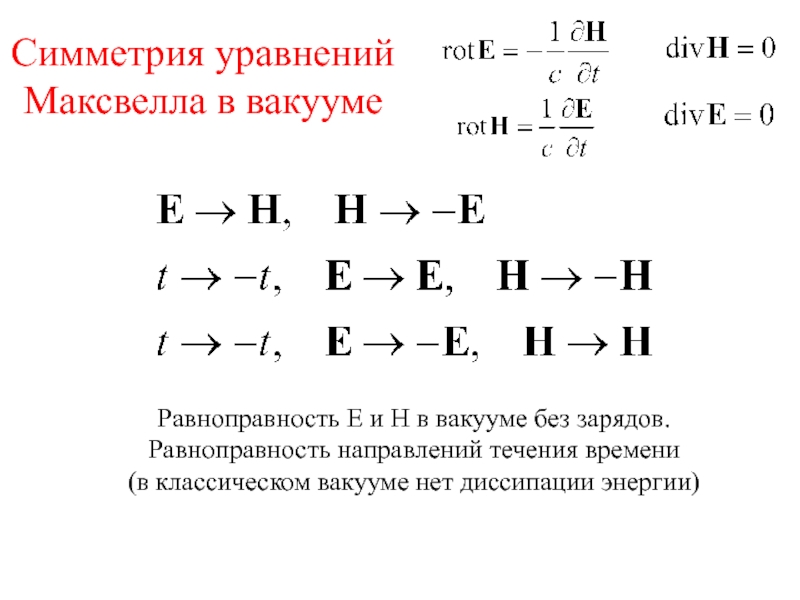
Слайд 15Симметрия уравнений Максвелла в вакууме
Равноправность Е и Н в вакууме
без зарядов.
Равноправность направлений течения времени
(в классическом вакууме нет диссипации
энергии)
Слайд 16Векторная структура уравнений Максвелла
ρ – скаляр (плотность эл. заряда)
E, D,
j – полярные трехмерные векторы
H, B – аксиальные трехмерные векторы
При
зеркальном отражении направление полярных векторов не меняется, а для аксиальных сменяется противоположным. Ср. с силой Лоренца
Различие полярных и аксиальных векторов существенно для записи нелинейных восприимчивостей.
Слайд 17Волновое уравнение
Немагнитные среды
Не все решения волнового уравнения служат решениями уравнений
Максвелла, поскольку эти решения могут не удовлетворять уравнению
. Фактически это соотношение накладывает ограничения на поляризационную структуру излучения. Таким образом, при исключении из уравнений Максвелла магнитных величин к волновому уравнению следует добавить уравнение
Слайд 18Динамика э.-м. поля
При заданных материальных соотношениях возможна постановка задачи Коши
– по начальным данным определяется последующие значения полей.
Динамических уравнений два
(содержащих временную производную 1-го порядка; частотной дисперсией здесь пренебрегаем). Два «статических» уравнения ограничивают вид начальных условий.
Пример – вакуум без зарядов ( )
Слайд 19Динамика э.-м. поля в вакууме
Уравнения Максвелла содержат производные по времени
первого порядка. Поэтому задания напряженностей Е и Н в начальный
момент времени достаточно для определения дальнейшей динамики поля (+ граничные условия).
Метод численного расчета: FDTD – finite-difference time-domain. – тема для итоговой презентации
Слайд 20Начальные условия (вакуум)
не произвольны. Они должны подчиняться условиям
Если это так,
то и в последующие моменты времени значения
останутся нулевыми, так
как {div rot V = 0}
Из-за уравнений Максвелла с div произвольно можно задавать только по две компоненты векторов Е0 и Н0, эти уравнения определяют вид третьих компонент. Например, пусть заданы
Тогда (f – произвольная функция своих аргументов)
Слайд 21Динамика поля (задача Коши)*
Поскольку уравнения Максвелла – первого порядка по
времени, то начальные условия позволяют определить значения напряженностей электрического и
магнитного полей в последующие моменты времени.
Разложения Тейлора для малых интервалов времени:
Слайд 25Эволюционная переменная, пример уравнения Гельмгольца
Однородная среда (вакуум), монохроматическое излучение с
частотой ω
Фиксированная (линейная) поляризация. Одна из компонент поля f
(пример Адамара)
Слайд 26Задача Коши для уравнения Гельмгольца
Рассмотрим пучок монохроматического излучения с преимущественным
направлением вдоль оси z
Зададим при z = 0 значения f
и
Решение уравнения Гельмгольца
(разделение переменных)
Слайд 27Задача Коши для уравнения Гельмгольца
Предел
При нулевых (в пределе) начальных данных
есть решение, стремящееся при конечных z к бесконечности. Но при
таких начальных данных есть и нулевое решение.
Нет непрерывной зависимости решения от начальных данных.
Постановка задачи некорректна.
Физ. смысл – встречные волны.
При конечных z
Слайд 28Ковариантная формулировка уравнений Максвелла в вакууме.
Тензоры электромагнитного поля
Напряженности электрического и
магнитного полей не абсолютны и имеют разную величину в различных
инерциальных системах отсчета, движущихся относительно друг друга со скоростью V.
Задача – показать релятивистскую инвариантность уравнений Максвелла и найти преобразования Лоренца для электромагнитного поля.
Форма записи уравнения будет релятивистски инвариантной, если оно записано в терминах скаляров, 4-векторов и тензоров, для которых известны преобразования Лоренца.
Слайд 29Ковариантная формулировка …*
Вводим 4-мерное пространство-время с координатами xk, k =
0, 1, 2, 3
Другая инерционная система координат
Преобразование Лоренца в частном
случае , когда скорость V имеет только x-компоненту
Слайд 304-векторы
Ковариантный 4-вектор (нижние индексы)
Контравариантный 4-вектор (верхние индексы)
Напряженности электрического и магнитного
полей не составляют 4-вектора.
Слайд 314-тензоры
ковариантный (нижние индексы)
контравариантный (верхние индексы)
Слайд 32Тензор электромагнитного поля
Антисимметрия
Слайд 33Преобразование Лоренца напряженностей э.-м. поля
(спец. случай)
Слайд 34Ковариантная форма уравнений Максвелла
Слайд 36Тензор энергии-импульса э.-м. поля
Симметрия по индексам ?
Символ Кронекера
при i = k и
0 в противном случае.
- плотность э.-м. энергии, - плотность потока энергии.
Тензор энергии-импульса (поля и среды) служит источником искривления пространства-времени в уравнениях тяготения Эйнштейна.
Слайд 37Задания
Найти напряженности электрического и магнитного полей точечного заряда, движущегося с
постоянной скоростью.
Проверить инвариантность величин
и (E,H).
Проверить, что ковариантная запись уравнений Максвелла приводит к стандартной записи при различном выборе индексов.
- это все дом. задания
Слайд 38Уравнение распространения фронта электромагнитной волны
Ранее мы решали задачу Коши, то
есть по начальным данным
(при t = 0) о напряженностях
поля определяли последующую
динамику поля. Это возможно, так как уравнения Максвелла в вакууме содержат только первые временные производные напряженностей. Более общая постановка задачи динамики:
Уч. пособие, стр. 13-17
Слайд 39Законы сохранения для э.-м. поля в вакууме
Уч. пособие, стр. 17-20
Слайд 40Потенциалы поля и волновое уравнение
Уч. пособие, стр. 20-22
Слайд 41Одномерное волновое уравнение - решение Даламбера
Уч. пособие, стр. 22-24.