Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
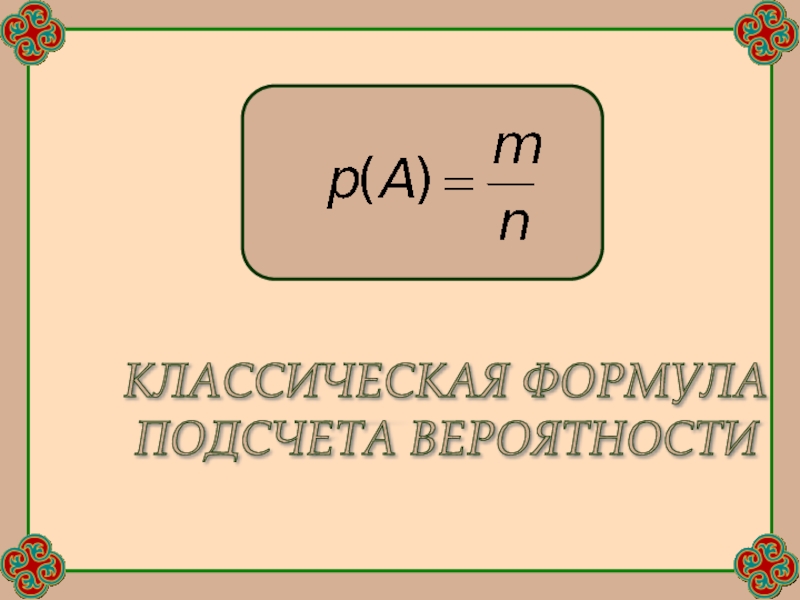
Классическая формула подсчета вероятностей
Содержание
- 1. Классическая формула подсчета вероятностей
- 2. Пример: выпадение герба и решки образуют полную
- 3. Случаем называются равновозможныепопарно несовместные события,образующие полную группу.Случай
- 4. При бросании игральной кости возможно 6
- 5. Вероятность события можно оценить по относительной доле
- 6. КЛАССИЧЕСКАЯ ФОРМУЛА ПОДСЧЕТА ВЕРОЯТНОСТИ
- 7. В качестве единицы измерения вероятности принимается вероятность
- 8. Классическая формула для вероятности справедлива только в
- 9. Пример.Брошены два игральных кубика.Найти вероятность событий: А-
- 10. Всего будет 36 событий, которые являются случаями,
- 11. Событию В благоприятно 6 случаев: (6;4), (4;6), (5;5), (5;6), (6;5), (6;6) т.е. m=6.
- 12. Скачать презентанцию
Пример: выпадение герба и решки образуют полную группу событий.Группа событий называется полной, если при проведении опыта всегда происходитодно из этих событий.
Слайды и текст этой презентации
Слайд 1
Пример: выпадение герба и решки при однократном бросании монеты.
3. КЛАССИЧЕСКАЯ
ФОРМУЛА ПОДСЧЕТА ВЕРОЯТНОСТЕЙ
в одном опыте.Слайд 2
Пример: выпадение герба и решки образуют полную группу событий.
Группа событий
называется
полной, если при проведении
опыта всегда происходит
одно из этих
событий. Слайд 3
Случаем называются равновозможные
попарно несовместные события,
образующие полную группу.
Случай называется благоприятным
некоторому
событию, если
наступление этого случая
влечет за собой наступление
данного события.
Слайд 4
При бросании игральной кости возможно 6 случаев, из которых
три случая будут благоприятны событию А - появлению четного числа
очков.Пример.
Слайд 5
Вероятность события можно оценить по относительной доле благоприятных случаев.
Если
n - общее число случаев, а m - число случаев,
благоприятных событию А, то вероятность события А может быть найдена по формуле:Слайд 7
В качестве единицы измерения вероятности принимается вероятность достоверного события. Т.е.
вероятность события, которое всегда происходит, полагается равной 1.
Вероятные но
недостоверные события будут иметь вероятность меньше 1.Вероятность невозможного события полагается равной 0.
Таким образом, вероятность любого события находится в интервале от 0 до 1.
Слайд 8
Классическая формула для вероятности справедлива только в том случае, если
все исходы опыта можно разделить на группы равновозможных случаев. Часто
это является следствием симметрии, которой обладает опыт.Слайд 9
Пример.
Брошены два игральных кубика.
Найти вероятность событий: А-
сумма выпавших очков
– четная,
В – произведение очков больше 20.
Слайд 10
Всего будет 36 событий, которые являются случаями, поскольку они равновозможны
и образуют полную группу, т.е. n=36.
Решение.
Событию А будет благоприятно 18
случаев, т.е. m=18.