Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кодирование с помощью порождающего полинома
Содержание
- 1. Кодирование с помощью порождающего полинома
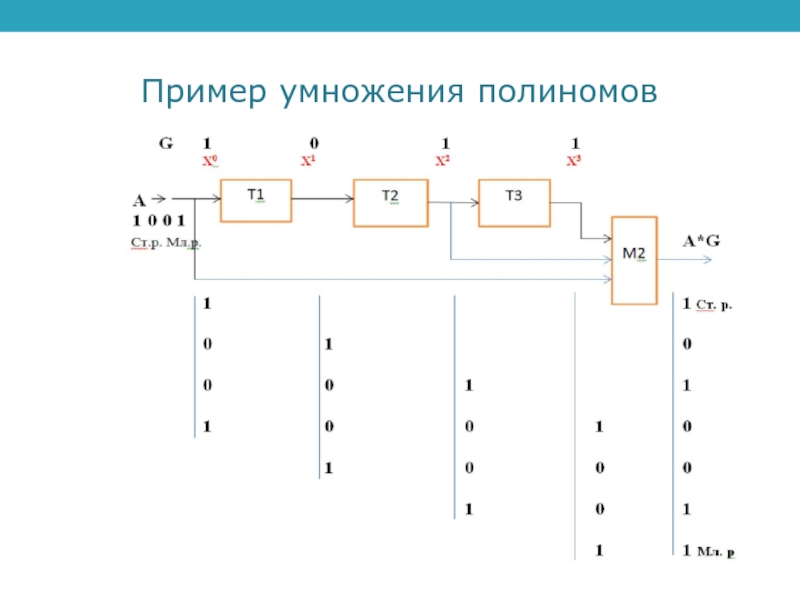
- 2. Пример умножения полиномовПример. Перемножить два полинома A
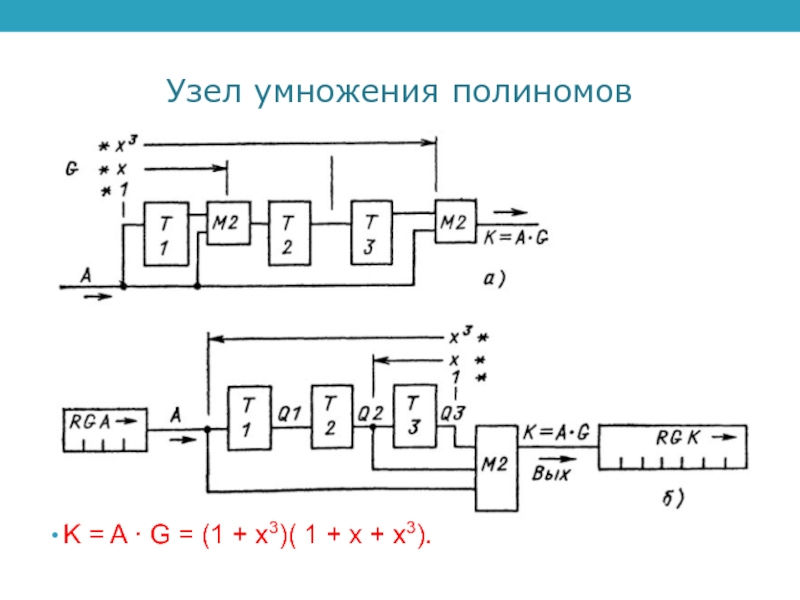
- 3. Узел умножения полиномовK = A · G
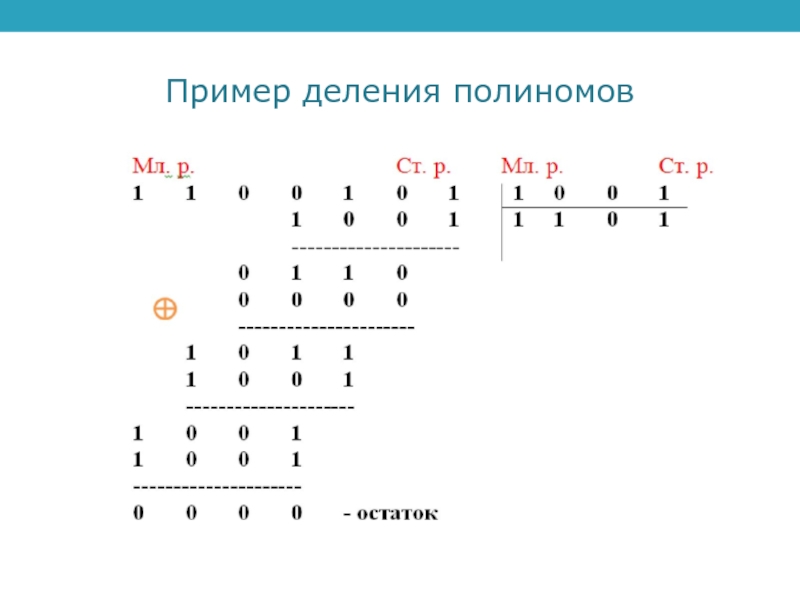
- 4. Пример деления полиномовВ результате получен код полинома К = 1101 и нулевой остаток.
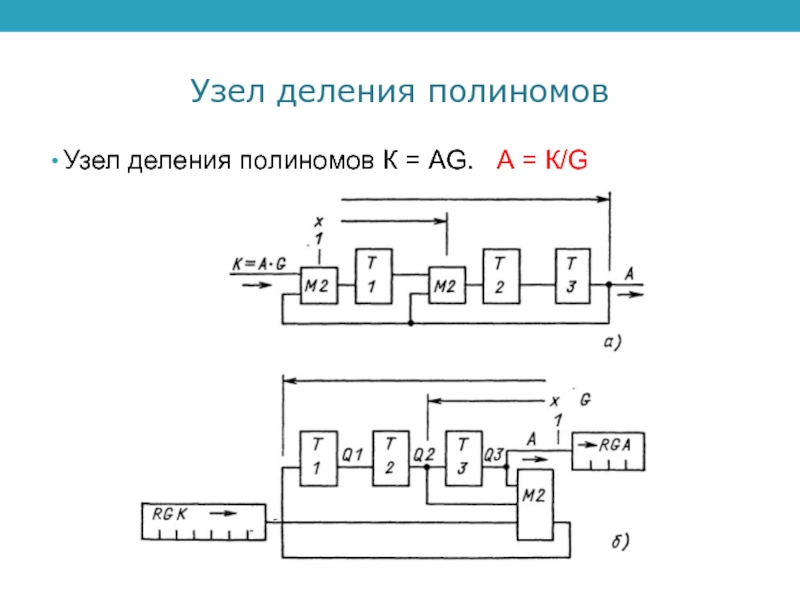
- 5. Узел деления полиномовУзел деления полиномов К = АG. А = К/G
- 6. Пример умножения полиномов
- 7. Пример умножения полиномов
- 8. Пример деления полиномов
- 9. Поля Галуа. Выполнение арифметических операцийб) перемножим полиномы:5
- 10. Поля Галуа. Порождающий полиномПродолжим вычисление произведения 5
- 11. Поля Галуа. Порождающий полиномТакой же результат можно
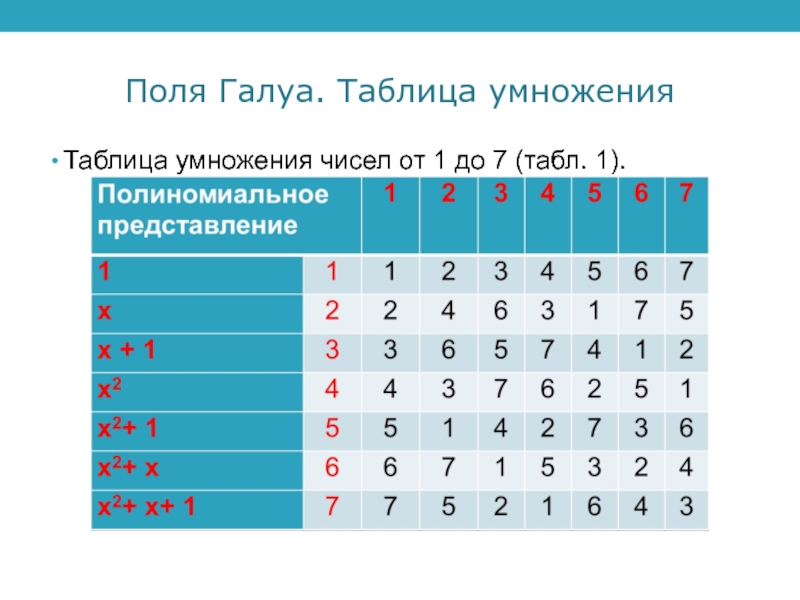
- 12. Поля Галуа. Таблица умноженияТаблица умножения чисел от 1 до 7 (табл. 1).
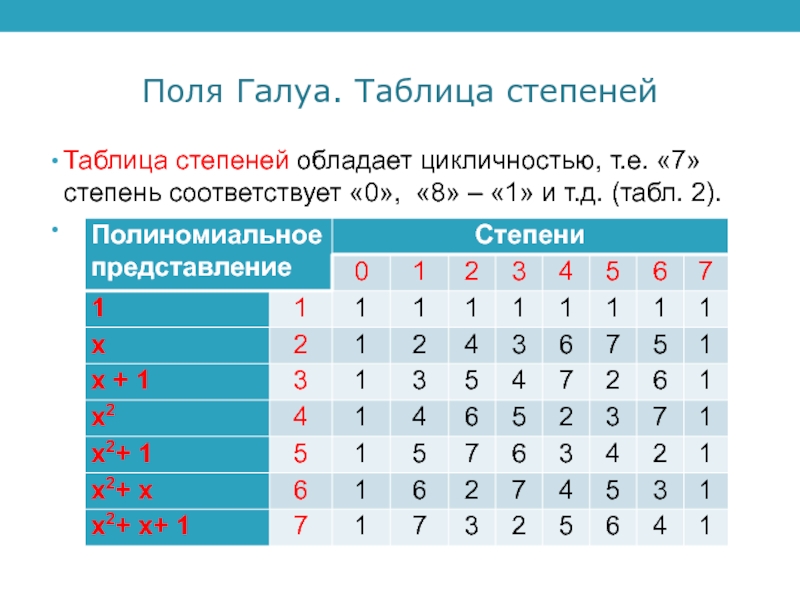
- 13. Поля Галуа. Таблица степенейТаблица степеней обладает цикличностью,
- 14. Поля Галуа. Пример 2. Вычислить значение 52
- 15. Поля ГалуаЛюбой элемент поля можно выразить через
- 16. Поля Галуа
- 17. Поля Галуа GF(28)Согласно теории, i-й элемент поля
- 18. Поля Галуа. GF(28)Правило первоначальной генерации поля:
- 19. Поля Галуа. GF(28)Правило построения поля:0-й элемент поля
- 20. Поля Галуа. GF(28)Символом обозначается операция XOR – побитовое сложение по модулю 2, а символом
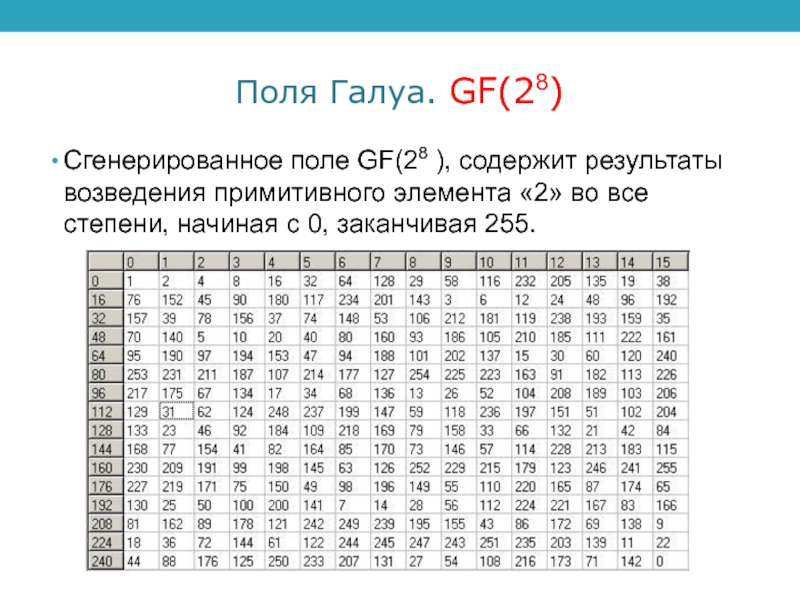
- 21. Поля Галуа. GF(28)Сгенерированное поле GF(28 ), содержит
- 22. Поля Галуа. GF(28)Вычисление значения 291 2 4 6 16
- 23. Поля Галуа. GF(28)Помимо основного поля в технологии
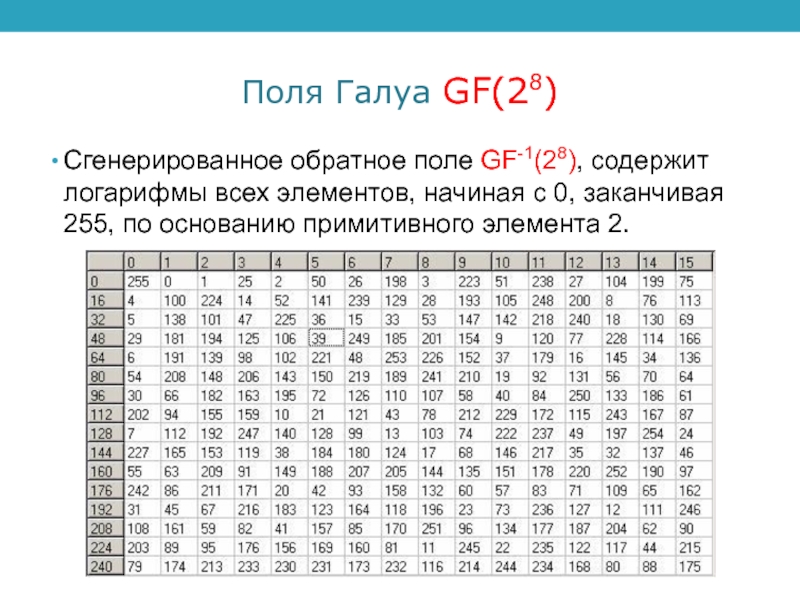
- 24. Поля Галуа GF(28)Сгенерированное обратное поле GF-1(28), содержит
- 25. Поля Галуа. Выполнение арифметических операцийОпределим четыре арифметические операции:
- 26. Поля Галуа. Выполнение арифметических операцийОперация деления:
- 27. Поля Галуа. Выполнение арифметических операцийВозведение в степень:Особенности
- 28. Поля Галуа. Выполнение арифметических операцийПримечания:Если сумма степеней
- 29. Поля Галуа. Выполнение арифметических операцийПример 2. Выполнение
- 30. Поля Галуа. Пример деления полиномовПример 2. Разделить
- 31. Поля Галуа. Пример деления полиномовПервый шаг
- 32. Поля Галуа. Пример деления полиномовВторой шаг
- 33. Поля Галуа. Пример деления полиномовТретий шаг
- 34. Поля Галуа. Пример деления полиномовПроверка:
- 35. Контрольные вопросы
- 36. Список использованных источников и литературыРахман П.А. Основы
- 37. Скачать презентанцию
Пример умножения полиномовПример. Перемножить два полинома A и G.K = A · G = (1 + х3)( 1 + х + х3).
Слайды и текст этой презентации
Слайд 9Поля Галуа.
Выполнение арифметических операций
б) перемножим полиномы:
5 · 7 = (х2
+ 1)( х2 + х +1) =
= х4 +
х3 + х2 + х2 + х + 1 == х4 + х3 + х + 1 =
= 110112 = 2710.
Слайд 10Поля Галуа. Порождающий полином
Продолжим вычисление произведения 5 и 7, добавив
слагаемые х2 + х + х2 + х, не меняющее
уравнение:5 · 7 =
= х4 + х3 + х + 1 =
= (х4 + х2 + х) + (х3 + х + 1) + х2 + х =
= x(х3 + х + 1) + (х3 + х + 1) + х2 + х =
= х2 + х = 1102 = 610.
Таким образом, результат умножения 5 · 7 = 6 принадлежит полю GF(23).
Слайд 11Поля Галуа. Порождающий полином
Такой же результат можно получить, вычислив остаток
от деления полинома, полученного при умножении, на порождающий полином
(х3
+ х + 1):Вывод: полученное значение произведения двух чисел 5 и 7 также принадлежит полю GF(23).
Слайд 13Поля Галуа. Таблица степеней
Таблица степеней обладает цикличностью, т.е. «7» степень
соответствует «0», «8» – «1» и т.д. (табл. 2).
Слайд 14Поля Галуа.
Пример 2. Вычислить значение 52 в полиноминальной форме.
52 = (х2 + 1)2 = х4 + х2 +
х2 + 1 = х4 + х2+ х + х2 + х + 1 == х(х3 + х + 1) + х2 + х + 1 = х2 + х + 1 = 1112 = 710.
При вычислении были добавлены значения х+х, а согласно определению х3 + х + 1 = 0.
Слайд 15Поля Галуа
Любой элемент поля можно выразить через степень примитивного полинома,
например: 5 = 26, 7 = 25. Рассмотрим примеры
выполнения арифметических операций по таблице степеней.Пример 3. Вычислить значение произведения двух чисел.
5·7 = 26 · 25 = 2(6+5) = 211 = 2(11 mod7)=24 = 6.
Слайд 17Поля Галуа GF(28)
Согласно теории, i-й элемент поля Галуа – это
результат возведения в i-ю степень некоторого примитивного элемента, в качестве
которого обычно берется простое число 2, где i = 0…28 – 1.Начиная i = 8, мы получим результат ,который уже выходит за пределы [0, 28 – 1] и здесь используется особый подход.
Слайд 19Поля Галуа. GF(28)
Правило построения поля:
0-й элемент поля это 1,
1-й элемент
– 2,
а, начиная со 2-го элемента по 254-й элемент,
элемент вычисляется как удвоенное значение предыдущего элемента, и если удвоение привело к числу, вышедшему заграницы 8-разрядов, то на него делается XOR с числом 28510 (11D16), наконец, последний 255-й элемент поля – 0. Число 285 – это десятичное представление (11D в
16 – ричном представлении) так называемого неприводимого полинома x8+x4+x3+x2+1, с помощью которого и порождается первоначальное поле.
Слайд 20Поля Галуа. GF(28)
Символом обозначается операция XOR – побитовое сложение по
модулю 2, а символом
представления числа на указанное количество разрядов.При этом биты, «вылезшие слева» из 8-разрядного байта, пропадают, а разряды, «освобождающиеся справа», заполняются нулями.
Сдвиг числа в двоичном представлении на один разряд влево– это эквивалентно удвоению числа.
Слайд 21Поля Галуа. GF(28)
Сгенерированное поле GF(28 ), содержит результаты возведения примитивного
элемента «2» во все степени, начиная с 0, заканчивая 255.
Слайд 22Поля Галуа. GF(28)
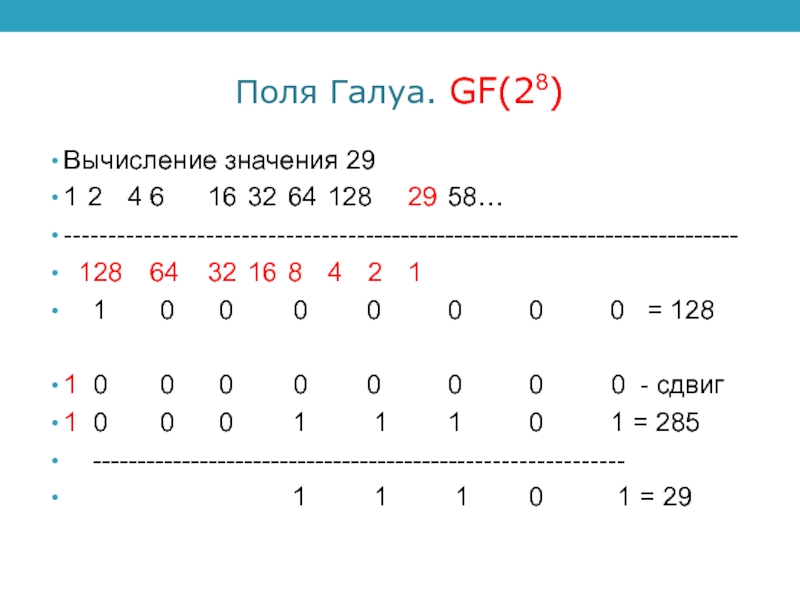
Вычисление значения 29
1 2 4 6 16 32 64 128 29 58…
----------------------------------------------------------------------------
128
64 32 16 8 4 2 1
1 0
0 0 0 0 0 0 = 1281 0 0 0 0 0 0 0 0 - сдвиг
1 0 0 0 1 1 1 0 1 = 285
------------------------------------------------------------
1 1 1 0 1 = 29
Слайд 23Поля Галуа. GF(28)
Помимо основного поля в технологии кодирования важно также
иметь и так называемое обратное поле, позволяющее по заданному значению
2k выяснить степень k, в которое был возведен примитивный элемент 2, иными словами иметь таблицу логарифмов пооснованию2.Обратное поле вычисляется следующим образом:
Слайд 24Поля Галуа GF(28)
Сгенерированное обратное поле GF-1(28), содержит логарифмы всех элементов,
начиная с 0, заканчивая 255, по основанию примитивного элемента 2.
Слайд 27Поля Галуа.
Выполнение арифметических операций
Возведение в степень:
Особенности выполнения арифметических операций.
Сложение и
вычитание для поля GF(28) заменяется побитовым сложением по mod2.
Так как
log(a ·b) = log a + log b и log (a/b) = log a - log b, то умножение (деление) сводится к вычислению log2 от операндов (по обратному полю Галуа), сложению (вычитанию) значений логарифмов и возведению в степень числа 2 суммы (разности) (по основному полю Галуа).Слайд 28Поля Галуа.
Выполнение арифметических операций
Примечания:
Если сумма степеней больше или равна 255,
то из нее вычитается 255.
Если сумма степеней меньше 0, к
ней прибавляется 255.При вычислении произведения степеней за результат берется остаток произведения по mod2.
Слайд 29Поля Галуа.
Выполнение арифметических операций
Пример 2. Выполнение условия а = (а/в)
· в,
например при а = 7 и в =
3.7 · 3 = 2^(log27 + log23) = 2^(198 + 25) = 2^(223) = 9.
9/3 = 2^(log29 – log23) =2^(223 - 25) – 2^(198) = 7.
Используем GF-1.
Слайд 30Поля Галуа.
Пример деления полиномов
Пример 2. Разделить полином А(х) на полином
g(х).
Делимое А(х) = 4х4 Å 2 х3 Å
х2 Делитель g(х) = х2 Å 2 х Å 2
Результат Q(х)
Остаток от деления R(х)
Слайд 36Список использованных источников и литературы
Рахман П.А. Основы защиты данных от
разрушения. Коды Рида-Соломона.- М.:МЭИ, 2007.
Потемкин И.С Функциональные узлы цифровой автоматики.
– М.: Энергоатомиздат, 1988. – 320 с.Открытые источники Internet.