Коллоидная химия

+ H2O + 2* 96500 Кл/ моль = Сu +

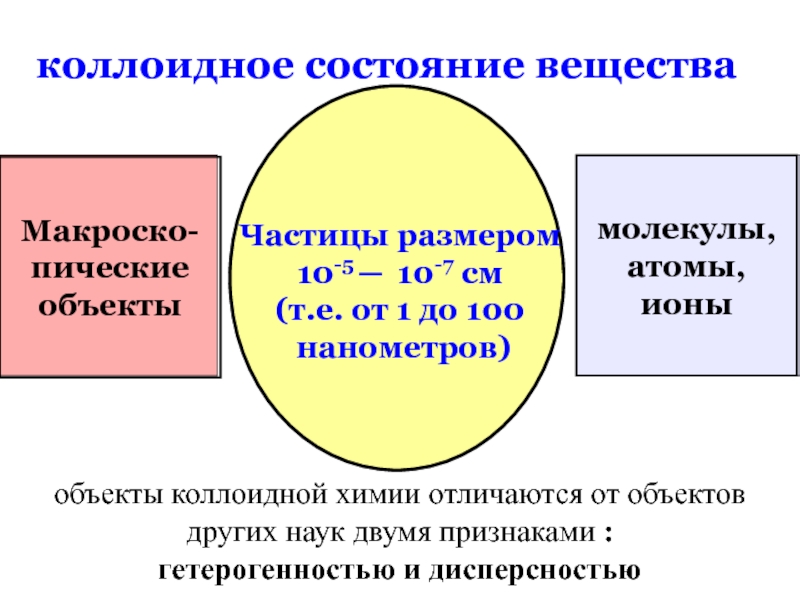
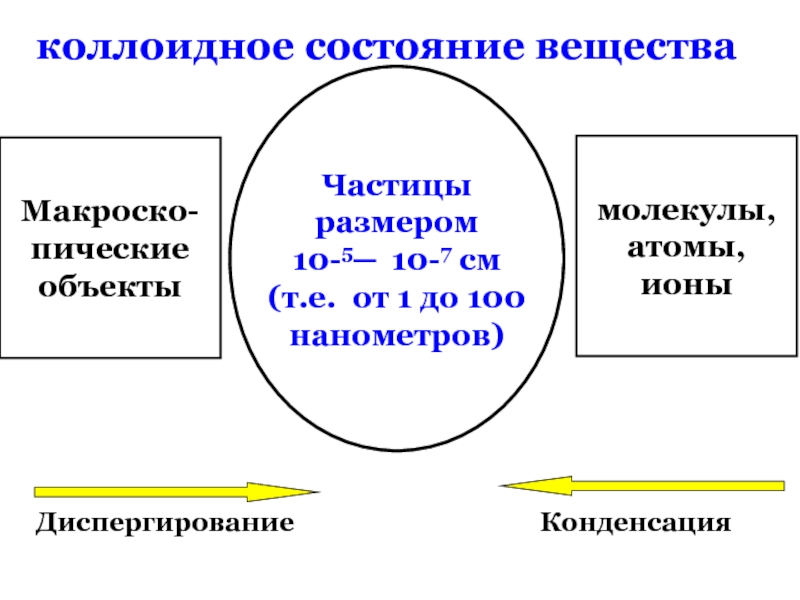
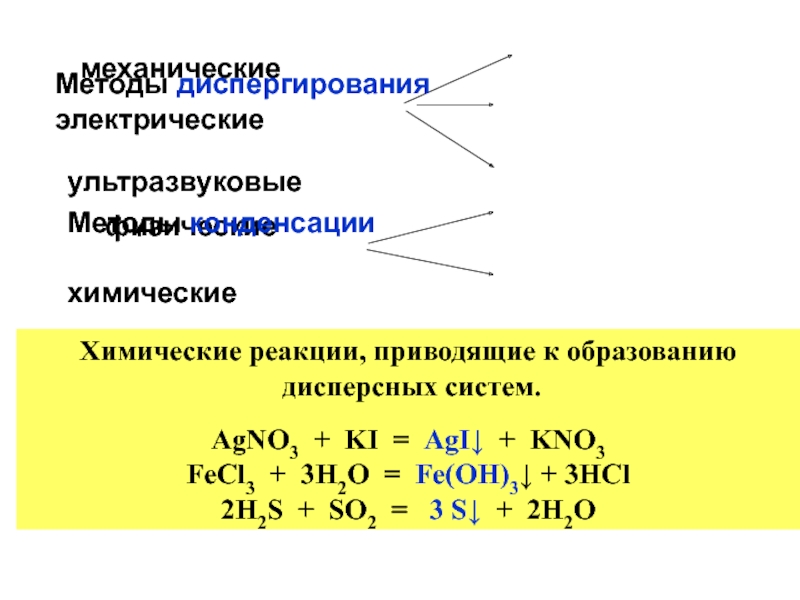
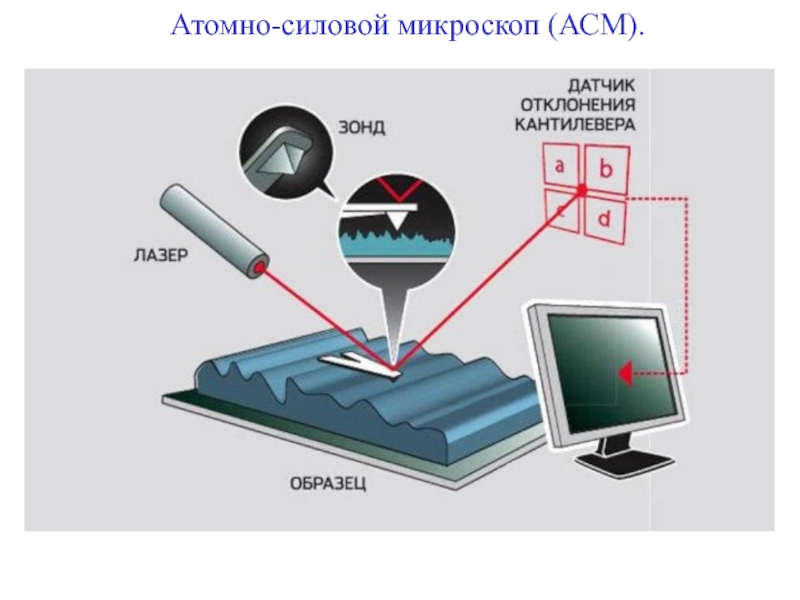
Физическая химия – наука, которая исследует взаимосвязь химических процессов и физических явлений, сопровождающих эти процессы .

В этой реакции выделяется энергия ( за счет которой и существуют живые организмы)

А для проведения этой реакции, напротив, необходимо затратить энергию

Большинство химических реакций связано с физическими явлениями ( выделение тепла, света, возникновение разности потенциалов и т.п.)

от 1 до 100
нанометров)
объекты коллоидной химии отличаются от

1г.
Площадь грани = 1см2
Суммарная площадь на 1г.т.е. S0= 6cм2
Разрежем каждую

0,5см

А если разрезать каждую грань на на 2,
а на миллион частей и сделать ребро кубика = 10-6см,
то величина S0 составит 600м2

Суммарный объем = 1см3
Суммарная масса = 1г
Площадь грани =0,25см2
Суммарная площадь
на 1 г, т.е. S0= 0,25*6*8=12cм2

В результате мы получим 2см2 новой поверхности

Если обозначить, что σ – энергия, необходимая для создания 1см2 новой поверхности,
то энергия, затраченная на разрыв стержня равна 2σ.

Вопрос : куда же делась затраченная нами энергия ?
Ведь согласно I началу термодинамики она не может исчезнуть, а может только перейти в другую форму.

тепловая поверхностная химическая
механическая электрическая
где : G - энергия Гиббса ; S – энтропия ; T – температура ;
V – объем ; P – давление ; σ - поверхностное натяжение ;
s – площадь поверхности ; μ i - химический потенциал ;
ni - число молей компонента ; φ - электрический
потенциал; q – количество электричества

i

Действительно, эта энергия осталась на образовавшейся новой
поверхности в виде свободной энергии Гиббса ( или Гельмгольца).
FS = σ * s .

Коллоидная химия - это физикохимия
поверхностных явлений
и гетерогенных высокодисперсных систем.

b) связно ─ дисперсные

3) по степени дисперсности :
Грубодисперные

Наиболее частый тип дисперсных систем – это суспензии, а если при этом частицы твердой фазы имеют коллоидные размеры, такие суспензии называют золями.

1 до 100 нанометров)

Методы диспергирования электрические

ультразвуковые

физические

Методы конденсации
химические

Химические реакции, приводящие к образованию
дисперсных систем.

AgNO3 + KI = AgI↓ + KNO3
FeCl3 + 3H2O = Fe(OH)3↓ + 3HCl
2H2S + SO2 = 3 S↓ + 2H2O

электродиализ

состава , а от числа кинетических единиц ( молекул или

К коллигативным свойствам относятся : понижение давления пара над раствором , изменение температур замерзания и кипения растворов , осмотическое давление.

Молекулярно-кинетические свойства
дисперсных систем.

эти свойства для частиц , занимающих промежуточное положение между более

Эти свойства были хорошо известны для истинных растворов и объяснены на основе молекулярно–кинетической теории , которая изучает законы самопроизвольного движения молекул .

Тем более , что до середины XIX века этих свойств у коллоидных растворов и не обнаруживали.

в 1827 г английским ботаником Р.Броуном непрерывного беспорядочного движения частиц

Для частиц , более крупных , чем коллоидные , в связи с большей их инерцией , вместо перемещения наблюдаются лишь малозаметные колебания .

Довольно быстро было установлено , что это движение никак не связано с процессами жизнедеятельности , с действием электрических сил или конвекцией , а вызвано беспорядочными ударами молекул дисперсионной среды о частицы дисперсной фазы .

сдвига частицы ∆х2 с коэффициентом диффузии , привели к созданию

Дело в том, что в середине XIX века высказывались серьезные сомнения в самом существовании молекул
(на том только основании , что их никто не видел)

приводящий к установлению одинаковых значений химического потенциала каждого компонента во

, т.к хаотическому распределению частиц соответствует максимальная энтропия системы.
Перенос

= RT/ 6πηrNA ,
из которого следует , что коэффициент

Коэффициент диффузии для молекул и ионов имеет порядок 10-5, а для коллоидных частиц 10-7―10-9 см2/с .

Для величины среднего квадратичного сдвига частицы в броуновском движении теория Эйнштейна – Смолуховского предлагает уравнение :
( III.4 ) ∆х2 = RTt / 3πηrNA
Сопоставляя два последних уравнения , находим :
( III.5 ) ∆х2 = 2Dt , т.е величина среднего сдвига частицы пропорциональна √ t .

вещества ρ , можно сначала , из уравнения (III.3) ,

Из уравнения (III.5) видно , что можно воспользоваться измерениями величины среднего сдвига частицы
для того , чтобы определить коэффициент диффузии .
С другой стороны , зная величины D,T и η , можно определить молекулярную массу ВМС.

раствора в раствор более высокой концентрации. В качестве полупроницаемой мембраны

Давление, которое необходимо создать со стороны раствора , чтобы приостановить осмос, называется осмотическим давлением .

За счет диффузии молекулы растворителя стремятся перейти в раствор, где их концентрация меньше. При этом объем раствора увеличивается

─ высота подъема жидкости,
необходимая для остановки осмоса

осуществляться не может, поэтому для разделения раствора на растворитель и

направление
течения воды через мембрану

размера и большие молекулы, например, молекулы сахарозы.
Но явление осмоса наблюдается

Почему через полупроницаемую перегородку проходят молекулы воды и не проходят ионы натрия или калия, значительно меньшие по размерам?

Ответ совсем простой и он понятен из следующего слайда.

4–8 молекул воды, и такое сложное образование значительно превышает по

т. к. оболочки клеток биологических тканей являются полупроницаемыми перегородками. Вследствие

Осмотическое давление внутри живых клеток обусловливает прочность и упругость тканей, и благодаря ему осуществляется солевой обмен живой ткани с окружающей средой ; идеальной полупроницаемой мембраной является протоплазма клеток..

с жидкостью , находящейся внутри эритроцитов и других клеток организма

Два раствора , имеющие одинаковое осмотическое давление , называются изотоническими растворами .

Осмотическое давление жидкостей организма человека равно осмотическому давлению 0,85% - ного раствора хлорида натрия, (так называемый физиологический раствор) и поддерживается постоянным за счет работы почек, удаляющих избыток воды или солей .

эритроциты сморщиваются, так как вода выходит из них в раствор.

Если эритроциты поместить в физиологический раствор, имеющий осмотическое давление, одинаковое с кровью, они не изменяют свой объем.

В гипотоническом растворе с более низким осмотическим давлением, чем давление крови, эритроциты набухают в результате перехода воды из раствора в клетку.

: концентрация соли в икринке – близка к океанической, а

В Черном море, из-за его низкой солености, не водятся каракатицы и кальмары, рыба-меч и рыба-шар, морские звезды и морские ежи ─ проплыть или проползти через Босфор из Мраморного моря в Черное они могут, а вот выжить там, а тем более принести потомство ─ нет.

Поэтому морские ежи и рыба-меч могут появляться в Черном море, но размножиться – не получится.

Чёрном море концентрация

Поэтому внутрь икринки устремляется вода
и вот результат ─ икринка лопается.

Π = сRT , где :
Π – осмотическое давление

Даже, если сделать скидку на приблизительность расчета, все равно это очень большая величина, которую невозможно не заметить в эксперименте .

Расчет по этому уравнению показывает , что для растворов неэлектролитов ( при с = 1 моль/л ;
R = 0,0821 атм*л/моль*K ; T= 273K )
осмотическое давление составит 22, 4 атм.

Впрочем, для растворов электролитов эта величина будет ещё больше, т.к. необходимо вводить поправку на изотонический коэффициент.

в два раза больше.
Аналогичные растворы СаСl2, Mg(NO3)2, Na2SO4 имеют

Следовательно, при нормальных условиях растворы неэлектролитов (сахарозы, глицерина, этанола), содержащие 1 моль вещества в 22,4 л раствора, имеют осмотическое давление 1 атм.

Дело в том, что осмос относится к коллигативным свойствам растворов, т.е. к свойствам, которые зависят только от числа кинетических единиц в объеме раствора.
Понятно, что при одинаковой концентрации в растворах электролитов число таких кинетических единиц будет больше, чем в растворах неэлектролитов.

(т.е. ионов) по сравнению с раствором неэлектролита аналогичной концентрации, и

Если молекула содержит n ионов, количество исходных молекул равно N, а степень диссоциации соединения ─ α, то количество диссоциировавших молекул равно N·α (при этом образуются N·α·n ионов), а общее количество частичек в растворе равно [(N — N·α) + N·α·n].

Изотонический же коэффициент равен отношению:

понятием концентрации дисперсной системы . Поскольку речь идет о кинетических

Почему же в течение столь длительного времени все исследователи не отмечали осмотического давления у коллоидных растворов ?

оказывается на семь порядков (!) меньше , чем молярная концентрация

 1атм = 10330 мм вод.ст. ;
т.е. (22,4*10,33*103) мм водн.ст. / 107 = 0,02

Проведем расчет осмотического давления для 0,1%-ного золя золота с размером частиц l = 10-6cм .

Для простоты будем считать частицы кубическими ,
а плотность золота , равной 20 г/см3.
Объем частицы = l 3 = 10-18cм3 ; масса = 2*10-17г.
В 1 л 0,1%-ного раствора содержится 1г золота,
т.е. 1/ ( 2*10-17 * 6*1023 ) ≈ 10-7 моль-частиц / л .

частиц золота, величины осмотического давления оказались более значительны . Так

Теперь становится понятно , почему столь малый подъем столба жидкости не замечали в течение длительного времени.

Из всего сказанного можно сделать следующий вывод : нет принципиальных различий в молекулярно-кинетических свойствах коллоидных и молекулярных растворов , просто вследствие огромной разницы в концентрациях кинетических единиц проявление этих свойств в коллоидных растворах гораздо слабее .

склонность к оседанию частиц дисперсной фазы , если плотность частиц

Смотрите , как уменьшается скорость оседания частиц кварцевого песка в воде с уменьшением их размеров

размера гравитационное поле , стремящееся создать разность концентраций по высоте

Поэтому в коллоидных системах устанавливается седиментационно – диффузионное равновесие .

Из курса физики известна барометрическая формула Лапласа , которая описывает распределение молекул идеального газа по высоте .
( III.10 ) ln P0/P1 = Mg(h1- h0) / RT
Перемещение 1 моля газа (М) от уровня Земли (высота h0) на высоту h1, где его потенциальная энергия равна Mgh1 - это работа изотермического сжатия 1 моля газа от давления Р0 до давления Р1 и она равна RTlnP0/P1 .

заменим отношение Р0 / Р1 на отношение числа частиц на

n0 mg(h1 – h0) NA (ρ1 – ρ0 )
(III.11) 2,3 lg = *
n1 RT ρ1

Мерой этой устойчивости является гипсометрическая высота – т.е. такая разность высот h1 – h0 , на которой концентрация дисперсной фазы изменяется в е раз .

с его помощью было впервые экспериментально найдено значение числа Авогадро

Исследуя с помощью микроскопа распределение частиц по высоте в монодисперсном золе мастики (гуммигута) , Перрен обнаружил , что их число частиц уменьшается вдвое через каждые 30 мкм .
Затем , по формуле (III.11) , Перрен вычислил значение числа Авогадро , которое оказалось равным 6,8 * 1023,

Позднее Вестгрен повторил опыт Перрена на золе золота, получив еще более точное значение числа Авогадро ─
6, 05 * 1023

За простоту , остроумие и точность этих опытов , в 1926 г
Перрену была присуждена

Нобелевская премия

движения частицы в жидкости , для сферической частицы будет выполнятся

А теперь разберем случай оседания частицы в жидкой дисперсионной среде :

(III.8) = 4/3 πr3*g*(ρ1 – ρ0) = 6πηru

Из этого соотношения легко выводится формула (III.9) , для определения радиуса оседающей частицы :

частиц в дисперсной системе и процентное содержание каждой фракции.
Наиболее частым

После определения начальной массы чашечки в воде и глубины её погружения h (см), можно получить седиментационную кривую, т.е. зависимость массы частиц, осевших на чашечку, от времени опыта t(с).

Образец такой кривой представлен далее.

кривой в точках, соответствующих различному времени опыта.
Для каждого времени t

Q,%

через каждые 2-5 мкм и составить следующую таблицу C(VI.3), что

можно провести дисперсионный анализ не только седиментационными, но и оптическими

являются коллоидными : земная атмосфера, облака, туманы, морская и речная

Дисперсные системы обладают не только фазовой, но и оптической неоднородностью . Лучи света , направленные на них , отражаются и преломляются под разными углами. Степень понижения интенсивности выходящих в прямом направлении лучей тем выше , чем больше дисперсность и концентрация дисперсной фазы

гомогенных систем ;
2) преломление и отражение света частицами дисперсной фазы

При падении луча света на дисперсную систему могут наблюдаться следующие явления :

Рассмотрим подробнее два последних случая , т.к. именно они наиболее характерны для коллоидных систем.

3) дифракция (рассеяние света) частицами дисперсной фазы ;
4) абсорбция (поглощение света) с превращением его в тепловую энергию.

дифракции его в микронеоднородной дисперсной системе , в тех случаях

Напомним , что видимая часть спектра находится в следующем диапазоне длин волн :
λкрасн. = 7,6*10-5см , а λфиолет. = 3,8*10-5см , следовательно , вся область коллоидного состояния вещества лежит вне этих пределов

При пропускании пучка света через коллоидную систему наблюдается образование светящегося конуса
( конус Тиндаля ) .

(убрав все , что можно в константу К ) :

1) Для частиц определенного размера Ip прямо пропорциональна концентрации золя. Этим можно воспользоваться для определения концентрации дисперсной фазы, измеряя светорассеяние нефелометром.

2) Интенсивность рассеянного света Ip прямо пропорциональна квадрату объема, (т.е. r6 ).
Следовательно , светорассеяние уменьшается как с уменьшением, так и с увеличением размера частиц (в этом случае оно переходит в отражение света) ; таким образом именно в области коллоидного состояния вещества наблюдается максимум интенсивности

мы увидим голубую окраску , а в направлении проходящего света

3) Интенсивность рассеянного света Ip обратно пропорциональна λ4 , т.е. рассеиваются главным образом более короткие волны (синяя область), а проходят через систему лучше более длинные (красная область) .

По этим же причинам лампы синего цвета применяют для светомаскировки , когда нужно , чтобы они оставались незамеченными с самолетов; а фонари желтого и красного цвета для сигналов опасности ( запрещающий сигнал светофора ) .

среды , поэтому если выбрать систему , где показатели преломления

Явление опалесценции внешне очень похоже на явление флуоресценции , которое обнаруживается у многих растворов красителей (эозина и флуоресцина) .
Однако эти явления совершенно различны по существу :

Флуоресценция –состоит в том, что молекулы вещества селективно поглощают свет определенной длины волны и превращают его в другой , с большей длиной волны .

Опалесценцию в коллоидной системе вызывает любой свет , тогда как флуоресценцию только свет определенной длины волны , характерной именно для данного вещества .

раствор интенсивность
на выходе может стать меньше по двум причинам

Для истинных растворов соотношение интенсивностей прошедшего ( Iпр ) и падающего света ( I0) зависит от толщины поглощающего слоя L и подчиняется закону Бугера - Ламберта :
(III.14) Iпр = I0 e-kL,
где : k - коэффициент поглощения

Ламберта – Бэра :

Бэр показал , что для раствора с абсолютно бесцветным и прозрачным растворителем коэффициент поглощения пропорционален молярной концентрации растворенного вещества :
(III.15) k = ε c .

данного вещества, зависящей от длины волны света, температуры , природы

Легко заметить , что при с =1 и L = 1 ,
величина ε = ln I0 / Iпр .
Если раствор не поглощает света , тогда ε = 0 , а значит , I0 = Iпр .

Iпр = I0 e ─ (ε + k) c L

Закон Бугера- Ламберта – Бэра может быть применен к коллоидным растворам, но с учетом того , что помимо абсорбции , в коллоидных растворах происходит “фиктивная абсорбция” , вызванная светорассеянием .

анализа , т.е определения размеров и формы частиц в системе

К оптическим методам относятся световая и электронная микроскопия , а также ультрамикроскопия . Световая микроскопия применима только для микрогетерогенных систем , с размерами частиц не менее 0,5 мкм ( 5*10-5см) . Частицы меньшего размера уже не отражают , а рассеивают свет видимой части спектра .

желтый

λ,
нм

Как видно из этого рисунка, область длин волн видимого света лежит в интервале 400 ─ 700 нм.
( а область коллоидного состояния начинается от 100 нм.)

Видимая часть спектра

λ
(III.20)

всё равно не удается довести нижний предел разрешающей способности до верхней границы коллоидной области , т.е. до 1* 10-5см .

Длина волны видимого света (400 – 700 ) нм .
Даже, если использовать все возможности формулы (20):
a) считать , что α = 1800 ; b) использовать масляную иммерсию , увеличив показатель преломления n до 1,5

оптический ультрамикроскоп, в котором дисперсная система освещается сбоку мощным потоком

В 1925 году он становится лауреатом Нобелевской премии по химии «за установление гетерогенной природы коллоидных растворов и за разработанные в этой связи методы, имеющие фундаментальное значение в современной коллоидной химии».

осветитель

окуляр

Применение ультрамикроскопа позволяет наблюдать частицы с размерами до 20-40нм, т.е. значительную часть коллоидной области.

Схема ультрамикроскопа

микроскопы (рис.VI.3),
в которых световой пучок заменяется потоком электронов.

Сильное электрическое поле с разностью потенциалов порядка 50 кВ ускоряет электроны до такой степени, что их длина волны соответствует нескольким ангстремам.

наблюдать гидрозоли и аэрозоли, а также живые объекты. Несмотря на

это
…. обычная…. блоха.
Кто это ???

так, как нам нужно?“ задал свой вопрос будущий Нобелевский лауреат

Тем не менее, когда в 60-е годы прошлого века впервые заговорили о нанотехнологиях, сразу встал вопрос о возможности наблюдения за поведением отдельных атомов.

Он же и подсказал одно из ключевых условий для открытия и исследований таких объектов: “Стократное превышение достигнутого разрешения электронного микроскопа“,

микромира удалось только тогда, когда на смену оптическому лучу пришла тончайшая

Атомно-силовая микроскопия позволяет анализировать на атомном уровне структуру самых разных твёрдых материалов — стекла, керамики, пластиков, металлов. Измерение можно проводить не тольков вакууме, но и на  
воздухе, в атмосфере любого газа и даже в капле жидкости.

до 10 нм). При перемещении микрозонда вдоль поверхности образца острие шипа приподнимается и опускается,

Микрозонд представляет собой тонкую пластинку-консоль (её называют кантилевером, от английского слова „cantilever“ — консоль, балка).

Смещая зонд по горизонтали, можно  с помощью компьютера построить трёхмерное изображение.

ученые из исследовательской лаборатории IBM в Цюрихе применив атомно-силовой микроскоп