Комбинаторика

Содержание

1. Комбинаторика
2. Комбинаторика - это раздел математики, в котором
3. Правило произведения.Если существует n вариантов выбора первого
4. Пример 2.В классе 20 учащихся. Необходимо назначить
5. Сколько существует шестизначных чисел, в которых все
6. Перестановки.Определение. Перестановками из n элементов называются соединения,
7. Пример 2. Сколько различных пятизначных чисел, не
8. Слайд 8
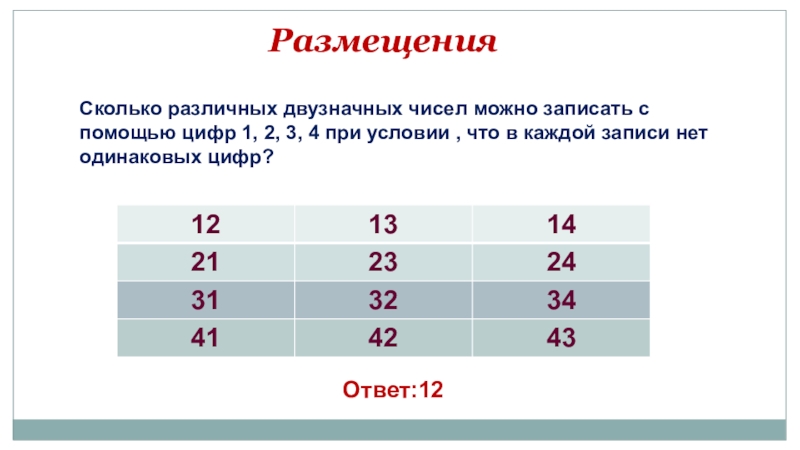
9. РазмещенияСколько различных двузначных чисел можно записать с
10. Определение.Размещением из m элементов по n элементов
11. 1. Сколькими способами можно обозначить данный вектор , используя буквы A, B, C, D, E, F?
12. Сколькими способами можно взять два фрукта из
13. Определение .Сочетаниями из m элементов по n
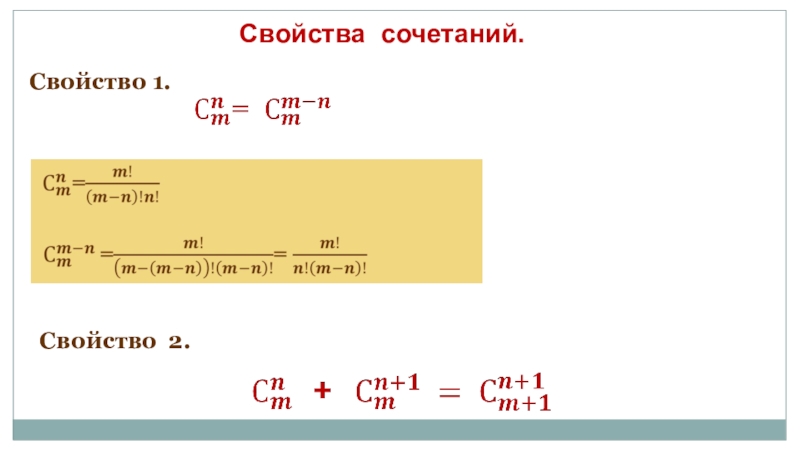
14. Свойства сочетаний.Свойство 1. Свойство 2.
15. Примеры: 1) вычислите2) Сколько существует
16. №1082(1) . Сколько аккордов , содержащих 4
17. Скачать презентанцию

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей

Слайды и текст этой презентации

Слайд 1Комбинаторика

Слайд 2Комбинаторика - это раздел математики, в котором изучаются вопросы о

том, сколько различных комбинаций, подчиненных тем или иным условиям, можно

составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или

Слайд 3Правило произведения.
Если существует n вариантов выбора первого элемента и для

каждого из них имеется m вариантов выбора второго элемента, то

всего существует n∙m различных пар с выбранными таким образом первым и вторым элементами.

Пример 1.

Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3 ?

В качестве первой цифры может быть выбрана любая из цифр 1, 2, 3 (т.е. n=3). Второй может быть любая из данных цифр, т. е. m=4.
По правилу произведения число всевозможных двузначных чисел равно m∙n = 3∙4 = 12. Ответ: 12.

Правило произведения.Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора

Слайд 4Пример 2.
В классе 20 учащихся. Необходимо назначить по одному дежурному

в столовую, вестибюль и спортивный зал. Сколькими способами это можно

сделать?

На первый пост можно поставить любого из 20 учащихся, (т.е. n=20 ), тогда на второй-любого из 19 оставшихся ( т.е. m=19 ), на третий пост остается выбрать любого из 18 учащихся ( к=18 ).

По правилу умножения возможное число способов

n∙m∙k = 20∙19∙18 = 6840.

Ответ: 6840.

Пример 2.В классе 20 учащихся. Необходимо назначить по одному дежурному в столовую, вестибюль и спортивный зал. Сколькими

Слайд 5Сколько существует шестизначных чисел, в которых все цифры стоящие на

четных местах различны?
Пример 3
1 - любая кроме ноля; 2 -

любая из десяти;
3 - любая из десяти; 4 - любая из девяти оставшихся;
5 - любая из десяти; 6 - любая из оставшихся восьми.

По правилу произведения можно составить

9 ∙10 ∙ 10 ∙ 9 ∙ 10 ∙ 8 = 648000

Сколько существует шестизначных чисел, в которых все цифры стоящие на четных местах различны?Пример 31 - любая кроме

Слайд 6Перестановки.
Определение. Перестановками из n элементов называются соединения, которые состоят из

одних и тех же n элементов и отличаются одно от

другого только порядком их расположения.
Pn=n(n-1)(n-2)(n-3)· … ·3 · 2 · 1
Pn = n!

Пример 1.
Сколькими способами можно разложить 6 открыток в 6 имеющихся конвертов.
6! = 1 · 2 · 3 · 4 · 5 · 6 = 720.

Ответ: 720.

Перестановки.Определение. Перестановками из n элементов называются соединения, которые состоят из одних и тех же n элементов и

Слайд 7Пример 2.
Сколько различных пятизначных чисел, не содержащих одинаковых цифр,

можно записать с помощью цифр 1,2,3,4,5 так чтобы первой была

цифра 4.

P4 = 4! = 1 · 2 · 3 · 4 = 24.

Ответ: 24.

Пример 2. Сколько различных пятизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1,2,3,4,5 так

Слайд 8

Слайд 9Размещения
Сколько различных двузначных чисел можно записать с помощью цифр 1,

2, 3, 4 при условии , что в каждой записи

нет одинаковых цифр?

Ответ:12

РазмещенияСколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии , что

Слайд 10Определение.
Размещением из m элементов по n элементов ( n ≤

m ) называются такие соединения, каждое из которых содержит n

элементов, взятых из данных m разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения .

Определение.Размещением из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из

Слайд 111. Сколькими способами можно обозначить данный вектор , используя буквы

A, B, C, D, E, F?

Слайд 12Сколькими способами можно взять два фрукта из вазы в которой

находятся яблоко, груша, банан, апельсин, мандарин и персик.
При размещении соединения

отличаются не только составом элементов но и порядком их расположения.

При решении этой задачи из 6 фруктов были образованы пары- соединения по 2 фрукта, которые отличаются только составом . Такие соединения называются сочетаниями.