Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Корень n -ой степени МБОУ СОШ №5 – Школа здоровья и развития г
Содержание
- 1. Корень n -ой степени МБОУ СОШ №5 – Школа здоровья и развития г
- 2. Понятие корня n-ой степениКорнем n-ой степени из
- 3. Примеры
- 4. Свойства корня n-ой степени (для n
- 5. Вычисление производной
- 6. Вычисление производной Примеры
- 7. Формула сложного радикалаПримеры
- 8. МБОУ СОШ №5 – «Школа здоровья и
- 9. Понятие степени с рациональным показателемПримеры
- 10. Свойства степени с рациональным показателем (для n ∈ R, k ∈ R)
- 11. Степенные функции y = x r Свойства
- 12. Степенные функции y = x r График
- 13. Степенные функции y = x r Свойства
- 14. Степенные функции y = x r График
- 15. Степенные функции y = x r Свойства
- 16. Степенные функции y = x r График
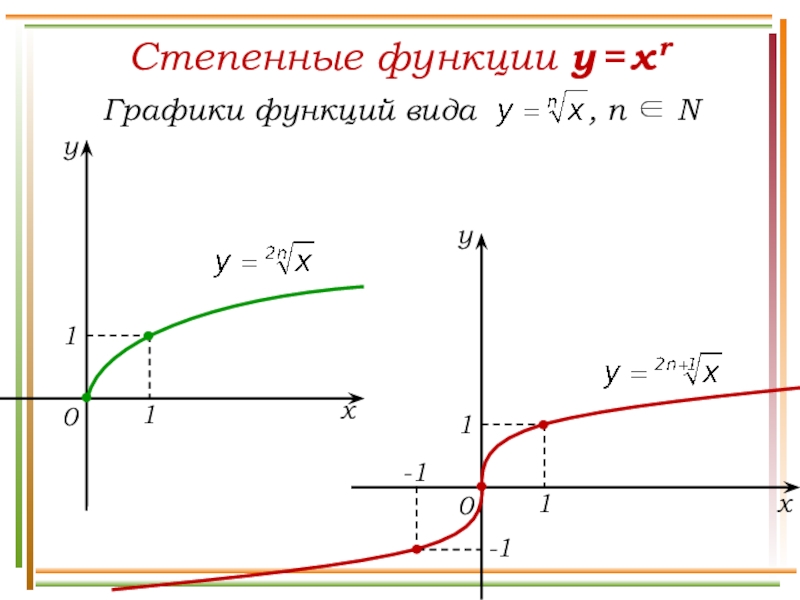
- 17. Степенные функции y = x r yx011yx011-1-1
- 18. Задания открытого банка задачРешение. Решение. Решение.
- 19. Задания открытого банка задачРешение. Решение. Решение.
- 20. Задания открытого банка задачРешение. Решение. Решение.
- 21. Задания открытого банка задачРешение. Решение.
- 22. Задания открытого банка задачРешение. Решение.
- 23. Скачать презентанцию
Понятие корня n-ой степениКорнем n-ой степени из неотрицательного числа а (n = 2, 3, 4, 5, ...) называют такое неотрицательное число, при возведении которого в степень п получается число а. Число
Слайды и текст этой презентации
Слайд 2Понятие корня n-ой степени
Корнем n-ой степени из неотрицательного числа а
(n = 2, 3, 4, 5, ...) называют такое неотрицательное
число, при возведении которого в степень п получается число а.Число а называют подкоренным числом,
а число n – показателем корня
Слайд 8МБОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
Степень
с рациональным показателем
Автор: Елена Юрьевна Семёнова
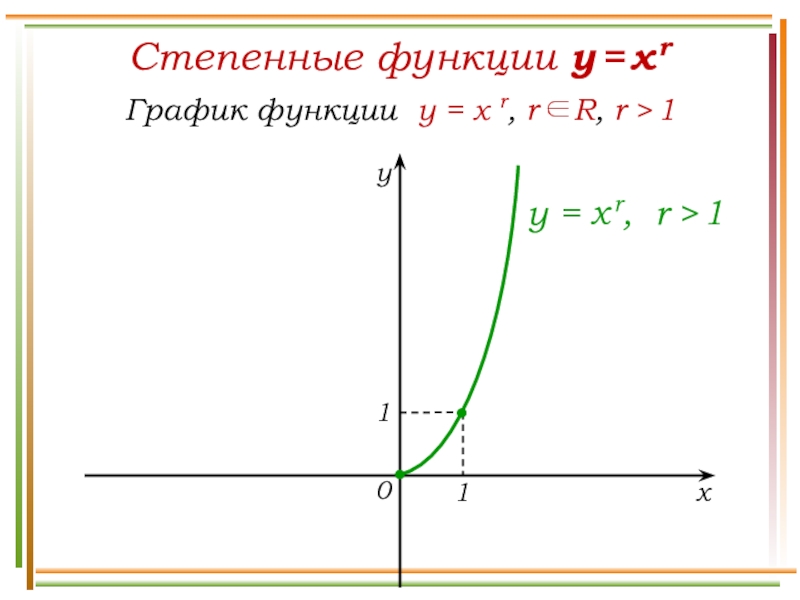
Слайд 11Степенные функции y = x r
Свойства функции y =
x r, r R, r > 1
D(у) = [0; +).
E(у) = [0; +).
Функция ни четная, ни нечетная.
а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
[0; +) – промежуток возрастания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; +).
Выпукла вверх.
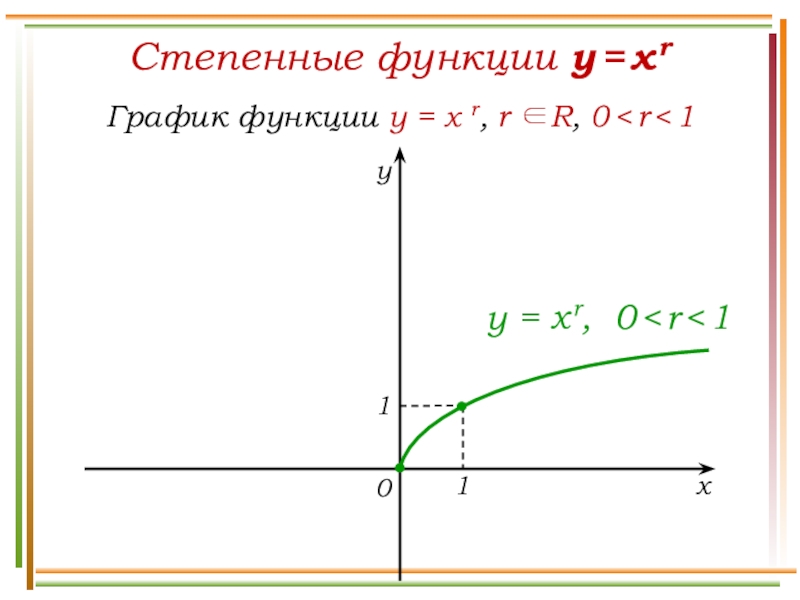
Слайд 13Степенные функции y = x r
Свойства функции y =
x r, r R, 0 < r < 1
D(у) =
[0; +). E(у) = [0; +).
Функция ни четная, ни нечетная.
а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
[0; +) – промежуток возрастания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. = 0;
б) унаиб. – не существует.
Непрерывна на множестве [0; +).
Выпукла вверх.
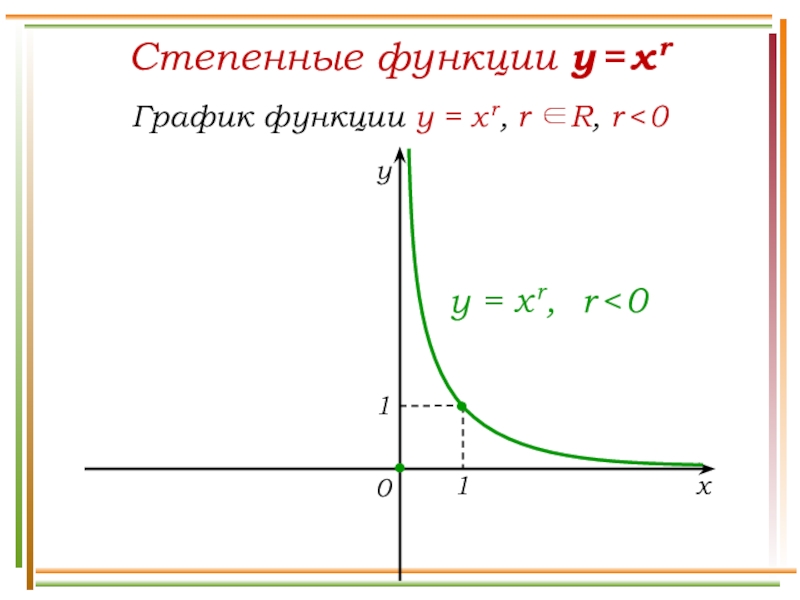
Слайд 15Степенные функции y = x r
Свойства функции y =
x r, r R, r < 0
D(у) = (0; +).
E(у) = (0; +).
Функция ни четная, ни нечетная.
а) Нули функции: нет.
б) Точка пересечения с Оу: нет.
(0; +) – промежуток убывания функции;
Ограничена снизу, не ограничена сверху.
а) унаим. – не существует;
б) унаиб. – не существует.
Непрерывна на множестве [0; +).
Выпукла вниз.