Коррекция нелинейных систем

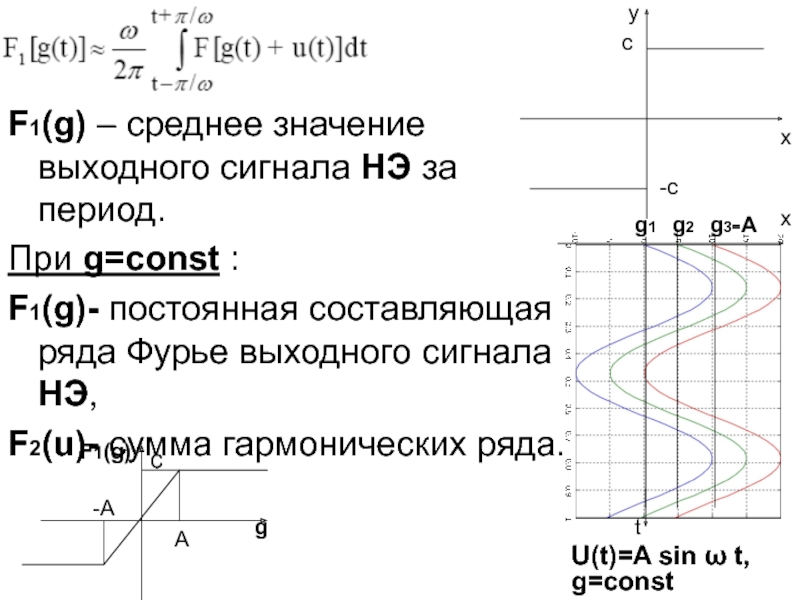
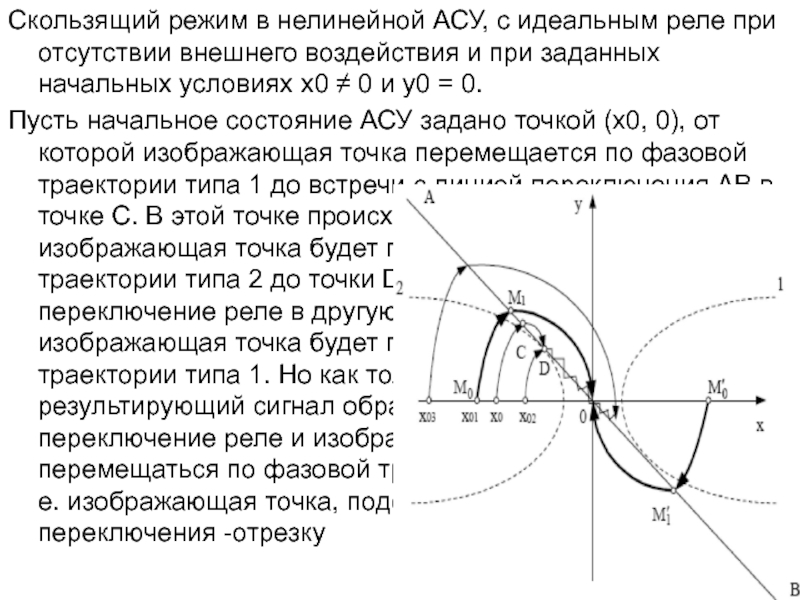
устойчивости системы;
получение автоколебаний (АК) с заданной амплитудой

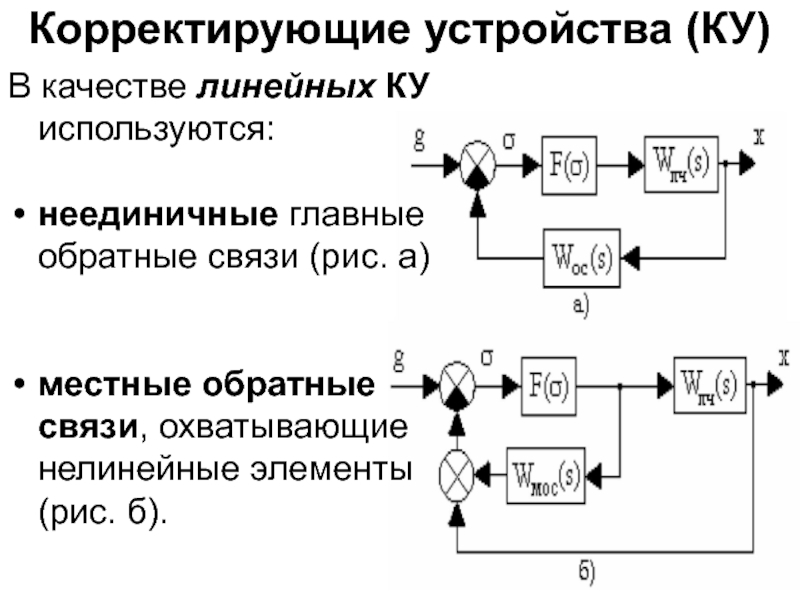
Аа и частотой Ω. Коррекция осуществляется с помощью
линейных или нелинейных корректирующих устройств (КУ),
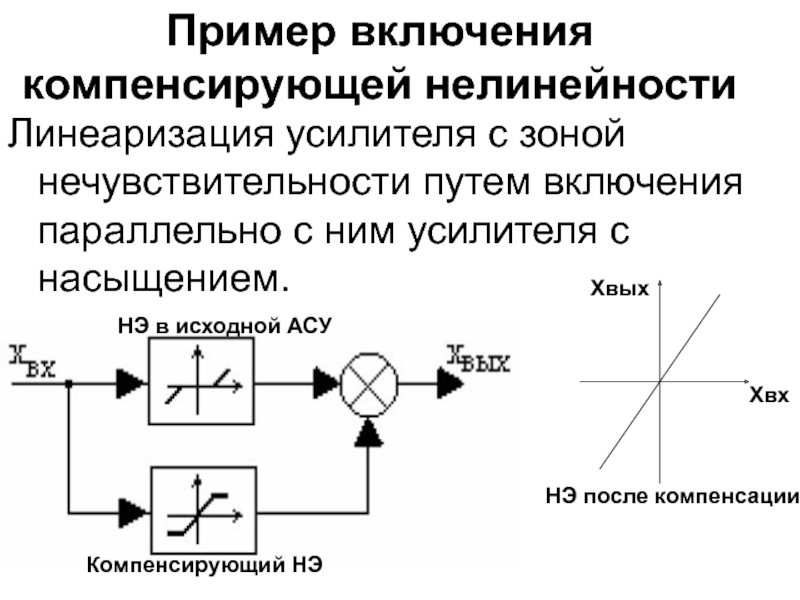
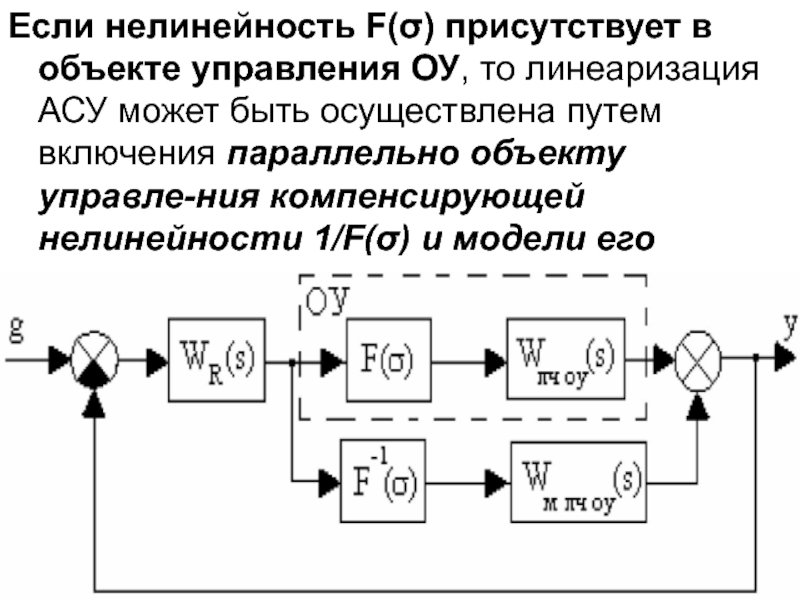
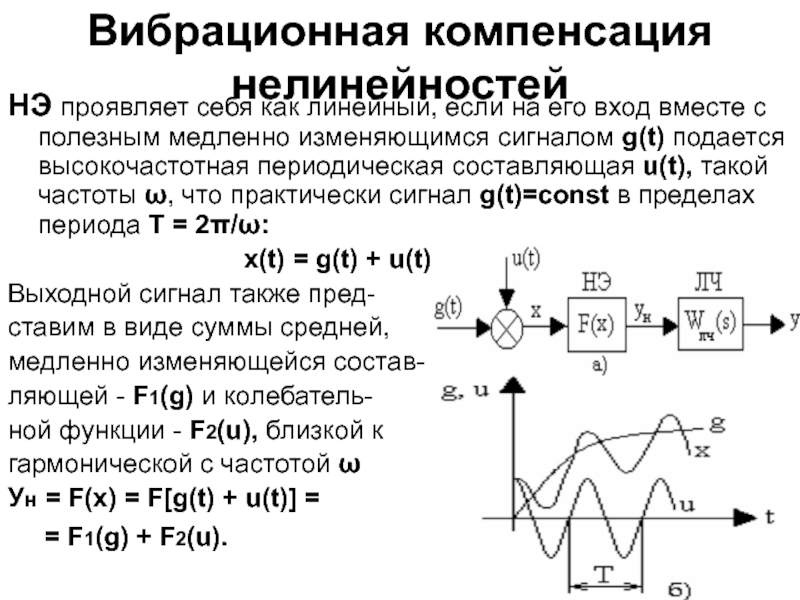
путем компенсации влияния нелинейностей.

(рис. а)


местные обратные связи, охватывающие нелинейные элементы (рис. б).

эквивалентной одноконтурной схеме с НЭ и эквивалентной линейной частью, с

передаточной функцией:
для схемы на рис.а:
W°л(s) = Wлч(s)*Wос(s);
для схемы на рис. б:
W°л(s) = Wлч(s) + Wмос(s).

относительно определенных входных воздействий.
В этом случае линеаризация заключается во

включении последовательно или параллельно заданной нелинейности F(σ) компенсирующего НЭ с обратной нелинейной характеристикой 1/F(σ). При этом получаем эквивалентный линейный элемент.

параллельно с ним усилителя с насыщением.



Хвых
Хвх
НЭ в исходной АСУ
Компенсирующий

НЭ

НЭ после компенсации

АСУ может быть осуществлена путем включения параллельно объекту управле-ния компенсирующей

нелинейности 1/F(σ) и модели его линейной части Wм.лч.оу(s)

вход вместе с полезным медленно изменяющимся сигналом g(t) подается высокочастотная

периодическая составляющая u(t), такой частоты ω, что практически сигнал g(t)=const в пределах периода T = 2π/ω:
x(t) = g(t) + u(t),
Выходной сигнал также пред-
ставим в виде суммы средней,
медленно изменяющейся состав-
ляющей - F1(g) и колебатель-
ной функции - F2(u), близкой к
гармонической с частотой ω
Ун = F(x) = F[g(t) + u(t)] =
= F1(g) + F2(u).

g=const :
F1(g)- постоянная составляющая ряда Фурье выходного сигнала НЭ,

F2(u)- сумма гармонических ряда.

y

x

x

t

c

-c

F1(g)

g

U(t)=A sin ω t, g=const

A

-A

g3=A

g2

g1

c

kу=c/A.
Чем больше A компенсирующих колебаний u(t), тем шире зона

линейности НЭ, но kу уменьшается.
Выходной сигнал НЭ- ун поступает на вход линейной части. При большой частоте ω сигнала u(t) линейная часть (фильтр) их не пропускает, поэтому составля-ющей F2(u) можно пренебречь и тогда для разомкну-той АСУ:
Wр(s) = y(s)/ g (s) = kу Wлч(s).
При задающем воздействии g(t) < A
на частоте, превышающей частоту среза линейной части ω> ωср, нелинейная АСУ ведет себя как линейная.
Для формирования высокочастотного сигнала u(t) используется специальный генератор или собственные колебания АСУ(скользящий режим).

точки вдоль линии переключения. Чем сильнее воздействие производной в цепи

обратной связи, тем боль-ше поворачиваются линии переключения реле против часовой стрелки. Интенсивность зату-хания переходного процесса возрастает. Скользящий режим возникает, если в точке переключения угол наклона линии переключения равен или меньше угла наклона касательной к фазовой траек-тории, по которой движется изобража-ющая точка после переключения реле.

внешнего воздействия и при заданных начальных условиях x0 ≠ 0

и y0 = 0.
Пусть начальное состояние АСУ задано точкой (x0, 0), от которой изображающая точка перемещается по фазовой траектории типа 1 до встречи с линией переключения AB в точке C. В этой точке происходит переключение реле и изображающая точка будет перемещаться по фазовой траектории типа 2 до точки D. В точке D происходит переключение реле в другую сторону, после чего изображающая точка будет перемещаться по фазовой траектории типа 1. Но как только увеличится результирующий сигнал обратной связи, произойдет переключение реле и изображающая точка будет перемещаться по фазовой траектории типа 2 и так далее, т.е. изображающая точка, подойдя к этому отрезку линии переключения -отрезку

Изобразим на фазовой плоскости

переходный процесс и АК в АСУ. Линейная часть задана:


Статическая характеристика НЭ:
yн = F(x).