Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Корреляционно-регрессионный анализ
Содержание
- 1. Корреляционно-регрессионный анализ
- 2. Содержание ВведениеВиды зависимостей, изучаемых в статистикеОсновные методы
- 3. ВведениеЯвления, которые в случае событий массового характера
- 4. Для исследования интенсивности, вида и формы причинных
- 5. Виды зависимостей, изучаемых в статистикеЗависимость одной случайной
- 6. Рассматривая зависимости между признаками, необходимо выделить прежде
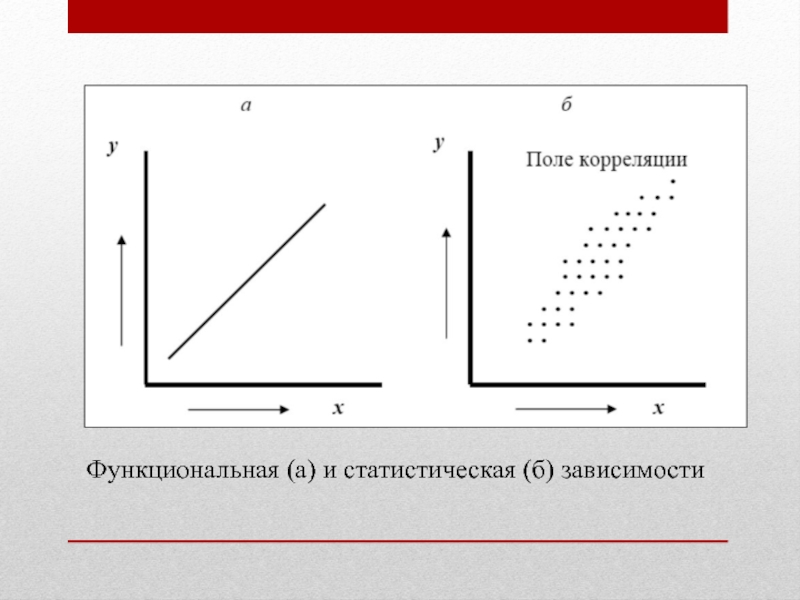
- 7. Функциональная (а) и статистическая (б) зависимости
- 8. Функциональная и статистическая зависимостиАналитически функциональная зависимость представляется
- 9. Рисунок 2. Поле корреляции
- 10. При исследовании корреляционных зависимостей между признаками решаются
- 11. Основные методы изучения взаимосвязейКорреляцию и регрессию принято
- 12. Методыметод сопоставления метод параллельных рядов балансовый метод
- 13. Слайд 13
- 14. Метод параллельных рядовМетод параллельных рядов – ряд
- 15. Метод аналитических группировокСущность этого метода заключается в
- 16. Слайд 16
- 17. Балансовый методСущность метода заключается в том, что
- 18. Слайд 18
- 19. Аналитический методИзучение корреляционных зависимостей основывается на исследовании
- 20. Важным этапом регрессионного анализа является определение типа
- 21. Слайд 21
- 22. Линейный коэффициент корреляции может принимать любые значения
- 23. Слайд 23
- 24. Проверка на адекватность регрессионной моделиДля практического использования
- 25. Слайд 25
- 26. Слайд 26
- 27. Экономическая интерпретация параметров уравнения регрессии После проверки
- 28. Слайд 28
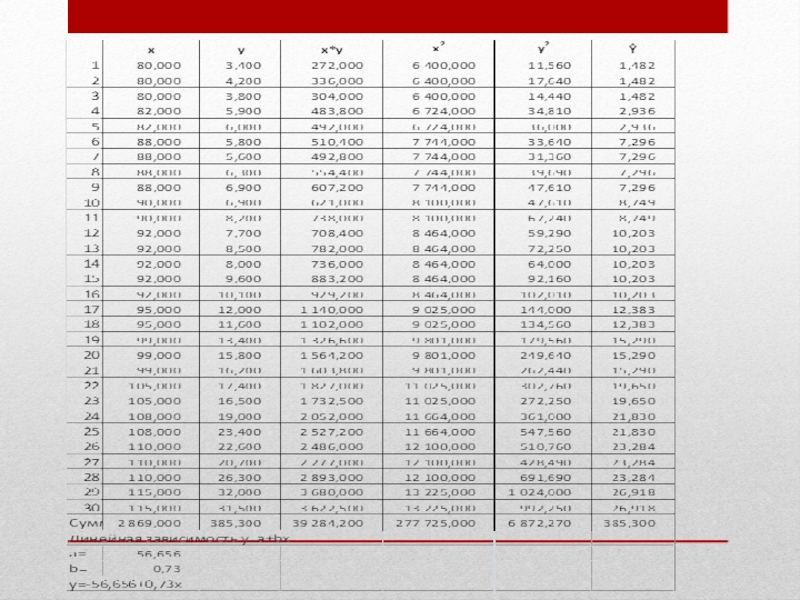
- 29. ЗаключениеПолученное уравнение y ̂=-56,656+0,73x позволяет проиллюстрировать зависимость
- 30. Спасибо за внимание
- 31. Скачать презентанцию
Содержание ВведениеВиды зависимостей, изучаемых в статистикеОсновные методы изучения взаимосвязейПроверка на адекватность регрессионной моделиЭкономическая интерпретация параметров уравнения регрессииЗаключение
Слайды и текст этой презентации
Слайд 2Содержание
Введение
Виды зависимостей, изучаемых в статистике
Основные методы изучения взаимосвязей
Проверка на
адекватность регрессионной модели
Слайд 3Введение
Явления, которые в случае событий массового характера отличаются определенной закономерностью,
однако не обнаруживаются на основе единичного наблюдения, называются массовыми явлениями.
Сама такая закономерность называется статистической закономерностью.Статистическая закономерность наблюдается в тех случаях, когда:
а) в исследуемом процессе действует один общий комплекс причин;
б) наряду с этим в каждом отдельном случае действуют особые дополнительные причины, всякий раз иные.
Слайд 4Для исследования интенсивности, вида и формы причинных связей широко применяется
корреляционный и регрессионный анализы.
Теория и методы корреляционного анализа используются
для выявления связи между случайными переменными и оценки ее тесноты. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными.
Слайд 5Виды зависимостей, изучаемых в статистике
Зависимость одной случайной величины от значений,
которые принимает другая случайная величина (физическая характеристика), в статистике называется
регрессией.Слайд 6Рассматривая зависимости между признаками, необходимо выделить прежде всего две категории
связи:
Функциональные – характеризуются полным соответствием между изменением факторного признака и
изменением результативной величины.Корреляционные (статистические) - рассматриваются как признак, указывающий на взаимосвязь ряда числовых последовательностей.
Слайд 8Функциональная и статистическая зависимости
Аналитически функциональная зависимость представляется в следующем виде:
y = f(x).
Графически статистическая зависимость двух признаков может быть
представлена с помощью поля корреляции, при построении которого на оси абсцисс откладывается значение факторного признака X, а по оси ординат – результирующего Y.Слайд 10При исследовании корреляционных зависимостей между признаками решаются следующие задачи:
1. Предварительный анализ
свойств моделируемой совокупности единиц.
2. Установление наличия связи в фактическом материале, определение
ее направления и формы.3. Измерение степени тесноты связи между признаками, т.е. степени приближения ее к функциональной зависимости.
4. Построение регрессионной модели, ее экономическая интерпретация и практическое использование.
Слайд 11Основные методы изучения взаимосвязей
Корреляцию и регрессию принято рассматривать как совокупный
процесс статистического исследования, поэтому их использование в статистике часто именуют
корреляционно-регрессионным анализом.Корреляционно-регрессионный анализ используется для исследования форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого процесса.
Слайд 12Методы
метод сопоставления
метод параллельных рядов
балансовый метод
графический метод
методы
аналитических группировок
метод дисперсионного анализа
метод корреляционного анализа
Слайд 14Метод параллельных рядов
Метод параллельных рядов – ряд значений факторного признака
и соответствующих ему значений результативного признака (значение признака Х располагается
в возрастающем порядке, затем прослеживают направление изменения величины результативного признака Y).Слайд 15Метод аналитических группировок
Сущность этого метода заключается в том, что единицы
статистической совокупности группируются, как правило, по факторному признаку и для
каждой группы исчисляется средняя или относительная величина по результативному признаку.Слайд 17Балансовый метод
Сущность метода заключается в том, что данные взаимосвязанных показателей
изображаются в виде таблицы и располагаются таким образом, чтобы итоги
между отдельными частями были равны, т.е. чтобы был баланс.Слайд 19Аналитический метод
Изучение корреляционных зависимостей основывается на исследовании таких связей между
переменными, при которых значение одной переменной можно принять за зависимую
переменную, которая «в среднем» изменяется в зависимости от того, какие значения принимает другая переменная, рассматриваемая как причина изменения зависимой переменной.Теоретической линией регрессии – называется линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи.
Слайд 20Важным этапом регрессионного анализа является определение типа функции, с помощью
которой характеризуется зависимость между признаками.
Тип уравнения выбирается на основе теоретического
анализа и исследования фактических данных. В большинстве случаев связи в общественных явлениях изучают по уравнению прямой, вида y=a+bx, где a и b – параметры искомой прямой.Слайд 22Линейный коэффициент корреляции может принимать любые значения в пределах от
-1 до +1. Чем ближе коэффициент корреляции по абсолютной величине
к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи: прямой зависимости соответствует знак «+», а обратной зависимости – знак «-».Зная коэффициент корреляции, можно дать качественно-количественную оценку тесноты связи. Используются, например, специальные табличные соотношения (так называемая шкала Чеддока).