Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Көпжақтар
Содержание
- 1. Көпжақтар
- 2. КөпжақтарЖазық көпбұрыштармен шектелген денелерді көпжақтар дейді. Олардың
- 3. Платон денелері деп аталатың бес дұрыс көпжақтар
- 4. додекаэдр (он екі жақты), жақтары тең қабырғалы он екі бесбұрыштан тұрады.
- 5. Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.
- 6. Тетраэдр (четырёхгранник)— многогранник с четырьмя треугольными гранями,
- 7. Гексаэдр (куб, hexa – шесть). Гексаэдр –
- 8. Октаэдр (греч. οκτάεδρον, от греч.
- 9. Додекаэдр (от греч. δώδεκα —
- 10. Икосаэдр (от греч. εικοσάς, «двадцать» и греч.
- 11. Кубооктаэдр — полуправильный многогранник, состоящий
- 12. В икосододекаэдре 30 одинаковых вершин, в которых
- 13. Кроме полуправильных многогранников из правильных многогранников -
- 14. Малый звездчатый додекаэдр(колючий еж)Большой додекаэдрБольшой звездчатый додекаэдрБольшой икосаэдр
- 15. Слайд 15
- 16. Көпжақтың сызбасыСызбада көпжақ – оның төбесінің және
- 17. Призмалық денеnlsn – бағыт-таушы;l – жасаушы;s- векторφ (l,n, s)MlM
- 18. Призмалық денеЕгер көпжақ призма бетімен және қырларына
- 19. Призманың сызбасыxA’2B’1C’2A1B2C1C’1B’2A’1B1A2C2M1M2l2l1
- 20. Пирамидалық денеSnln- бағыттаушыl- жасаушыS –тұрақты нүктеMlMΦ (n,l, S)
- 21. Пирамиданың сызбасыS2S1A2B2C2C1B1A1l2l1
- 22. Скачать презентанцию
КөпжақтарЖазық көпбұрыштармен шектелген денелерді көпжақтар дейді. Олардың жазық көпбұрышын жақ деп, өзара қиылысу түзулерін қыр деп атайды.
Слайды и текст этой презентации
Слайд 2Көпжақтар
Жазық көпбұрыштармен шектелген денелерді көпжақтар дейді. Олардың жазық көпбұрышын жақ
деп, өзара қиылысу түзулерін қыр деп атайды.
Слайд 3Платон денелері деп аталатың бес дұрыс көпжақтар бар, олар:
тетраэдр (төрт
жақты), жақтары тең қабырғалы төрт үшбұрыштан тұрады;
гексаэдр (алты жақты), жақтары
алты квадраттан тұрады;октаэдр (сегіз жақты), жақтары тең қабырғалы сегіз үшбұрыштан тұрады;
икосаэдр (жиырма жақты), жақтары тең қабырғалы жиырма үшбұрыштан тұрады;
Слайд 5Правильным многогранником называется многогранник, у которого все грани правильные равные
многоугольники, и все двугранные углы равны.
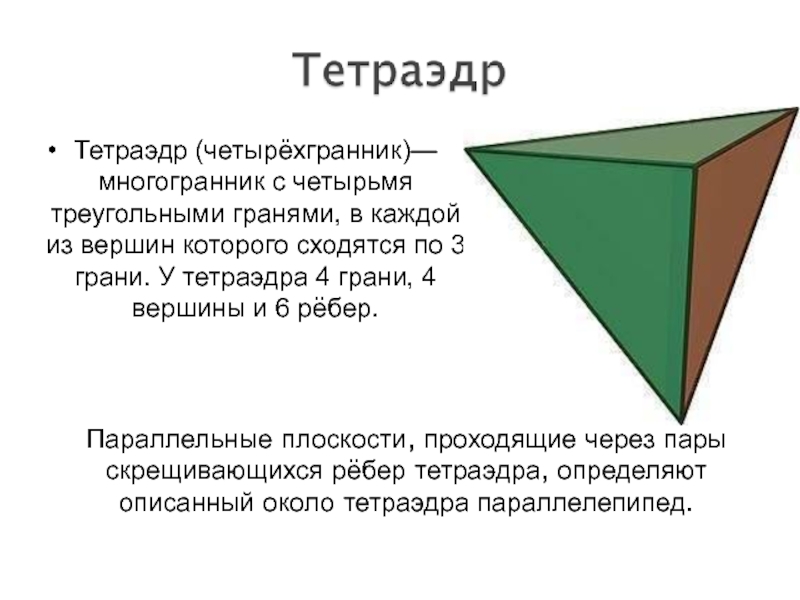
Слайд 6Тетраэдр (четырёхгранник)— многогранник с четырьмя треугольными гранями, в каждой из
вершин которого сходятся по 3 грани. У тетраэдра 4 грани,
4 вершины и 6 рёбер.Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
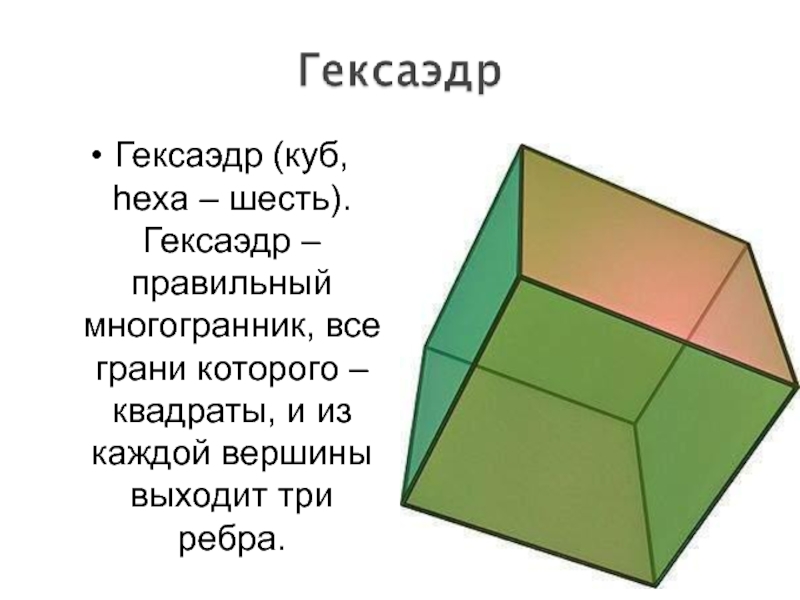
Слайд 7Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все
грани которого – квадраты, и из каждой вершины выходит три
ребра.
Слайд 8 Октаэдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и
греч. έδρα — «основание») — один из пяти выпуклых правильных
многогранников, так называемых, Платоновых тел.Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
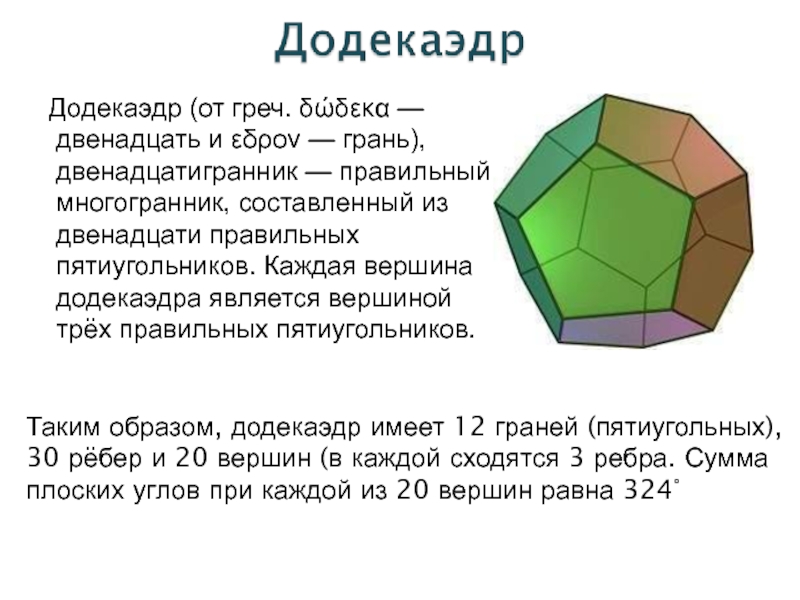
Слайд 9 Додекаэдр (от греч. δώδεκα — двенадцать и εδρον
— грань), двенадцатигранник — правильный многогранник, составленный из двенадцати правильных
пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра. Сумма плоских углов при каждой из 20 вершин равна 324°
Слайд 10Икосаэдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо»,
«основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Слайд 11 Кубооктаэдр — полуправильный многогранник, состоящий из 14 граней
(8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых
вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Двойственный к кубооктаэдру многогранник — ромбододекаэдр.
Слайд 12В икосододекаэдре 30 одинаковых вершин, в которых сходятся два треугольника
и два пятиугольника, а также 60 одинаковых рёбер, каждое из
которых разделяет треугольник и пятиугольник.Икосододекаэдр — полуправильный многогранник, состоящий из 32 граней (12 правильных пятиугольников и 20 правильных треугольников).
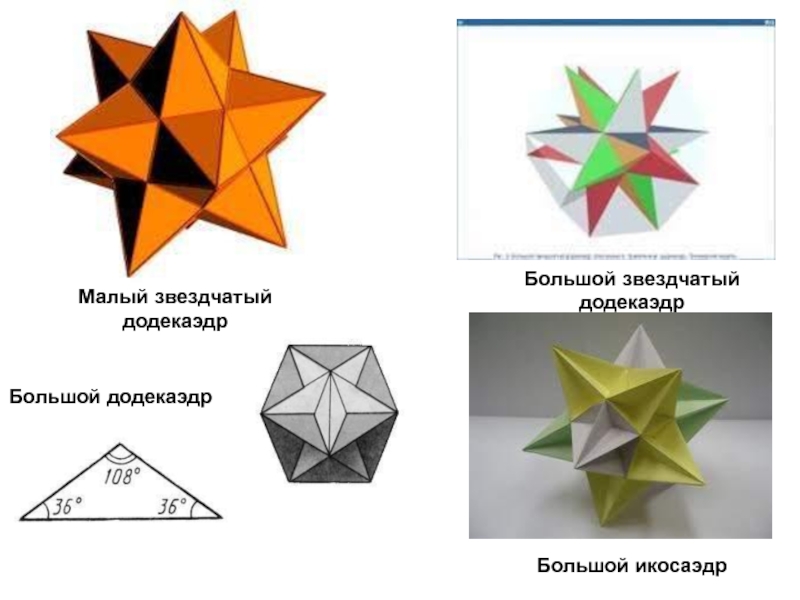
Слайд 13Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно
получить так называемые
правильные звездчатые многогранники.
Их всего четыре, они
называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр.
Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.
Слайд 14Малый звездчатый додекаэдр
(колючий еж)
Большой додекаэдр
Большой звездчатый додекаэдр
Большой икосаэдр
Слайд 16Көпжақтың сызбасы
Сызбада көпжақ – оның төбесінің және қырларының проекциялары арқылы
беріледі, немесе олардың проекцияларын тұрғызу нүктенің және түзудің кесінділерін тұрғызу
арқылы орындалады. Көпжақтардың ішінде көбірек тарағандары жәй көпбұрыштардан тұратын пирамида және призма түрлері.
Слайд 18Призмалық дене
Егер көпжақ призма бетімен және қырларына параллель емес екі
өзара параллель жазықтықтарымен шектелсе, онда мұндай көпжақты призма деп атайды.
