Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Критерии различий
Содержание
- 1. Критерии различий
- 2. Сравнение более двух независимых выборокКритерий H Краскала-УоллесаКритерий
- 3. гдеN – суммарная численность всех выборокk –
- 4. Ho: Отсутствуют статистически достоверные различия между выборками.H1: Имеются статистически достоверные различия между выборками.
- 5. Чем сильнее различаются выборки, тем больше вычисленное
- 6. Если сравниваются 3 выборки и объем каждой
- 7. Слайд 7
- 8. Слайд 8
- 9. 1. Значения выборок объединяются в один ряд,
- 10. 4. Вычисляется H по формуле.5. Определяется p-уровень значимости.6. Принимается статистическое решение.H=6,575
- 11. Слайд 11
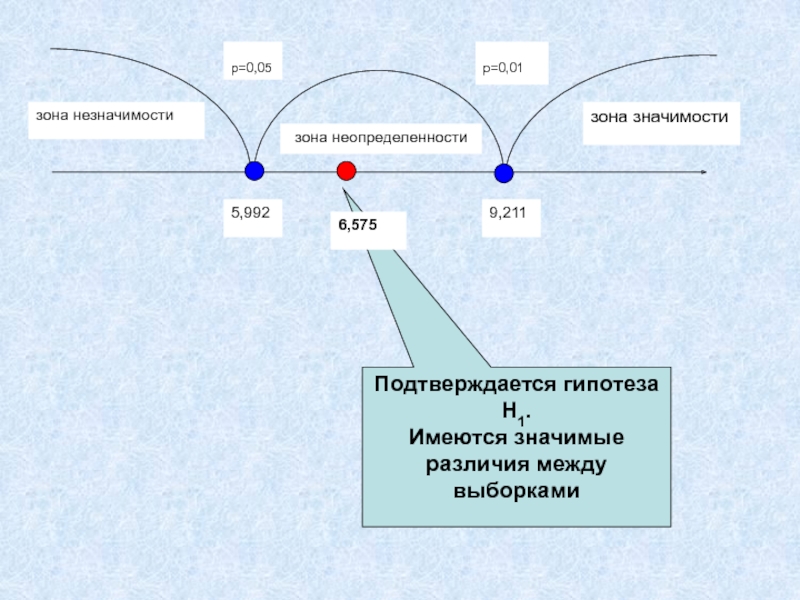
- 12. зона значимостизона незначимостизона неопределенностиp=0,05p=0,015,9929,211Подтверждается гипотеза H1.Имеются значимые различия между выборками6,575
- 13. Сравнение более двух зависимых выборокНепараметрический критерий χ2-Фридмана (хи-квадрат).Аналог – однофакторный дисперсионный анализ ANOVA для повторных измерений.
- 14. гдеN – число объектов (испытуемых)k – количество условий (повторных измерений)Ri – сумма рангов для условия i
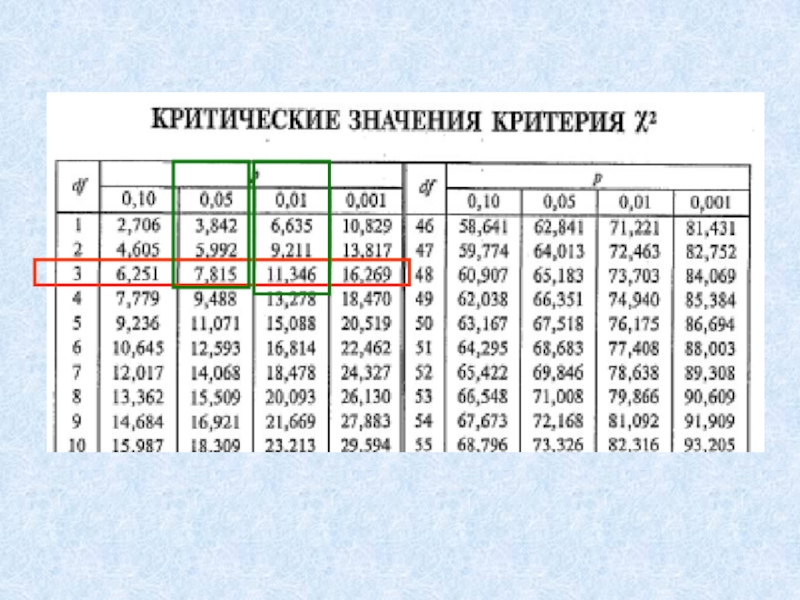
- 15. Если k=3, N>9 или k>3, N>4, то пользуются обычной таблицей для χ2.Если k=3, N
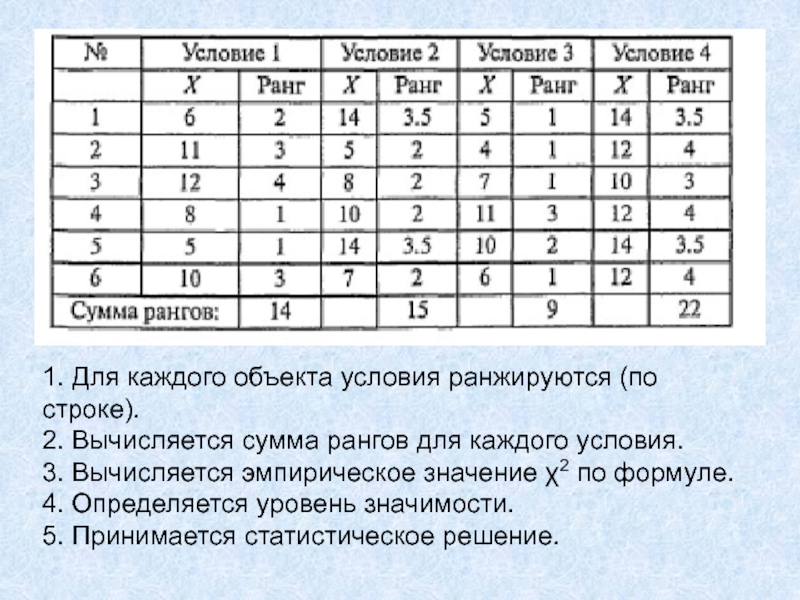
- 16. 1. Для каждого объекта условия ранжируются (по
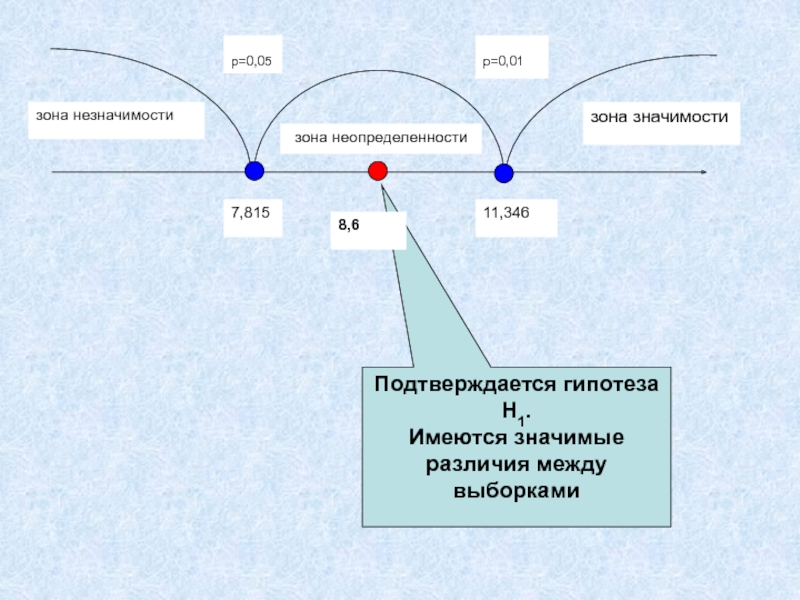
- 17. χ2=8,6df=3
- 18. Слайд 18
- 19. зона значимостизона незначимостизона неопределенностиp=0,05p=0,017,81511,346Подтверждается гипотеза H1.Имеются значимые различия между выборками8,6
- 20. Скачать презентанцию
Сравнение более двух независимых выборокКритерий H Краскала-УоллесаКритерий является непараметрическим.Аналог – однофакторный дисперсионный анализ ANOVA для независимых выборок.
Слайды и текст этой презентации
Слайд 2Сравнение более двух независимых выборок
Критерий H Краскала-Уоллеса
Критерий является непараметрическим.
Аналог –
однофакторный дисперсионный анализ ANOVA для независимых выборок.
Слайд 3где
N – суммарная численность всех выборок
k – количество сравниваемых выборок
Ri
– сумма рангов для выборки i
ni – численность выборки i
Слайд 4Ho: Отсутствуют статистически достоверные различия между выборками.
H1: Имеются статистически достоверные
различия между выборками.
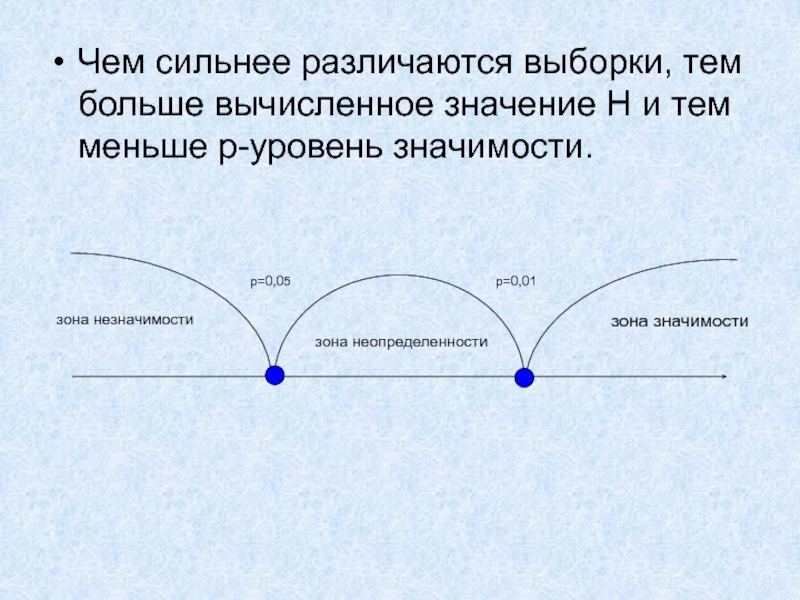
Слайд 5Чем сильнее различаются выборки, тем больше вычисленное значение H и
тем меньше p-уровень значимости.
зона значимости
зона незначимости
зона неопределенности
p=0,05
p=0,01
Слайд 6Если сравниваются 3 выборки и объем каждой выборки меньше 5,
то пользуются таблицей критических значений H-Краскала-Уоллеса.
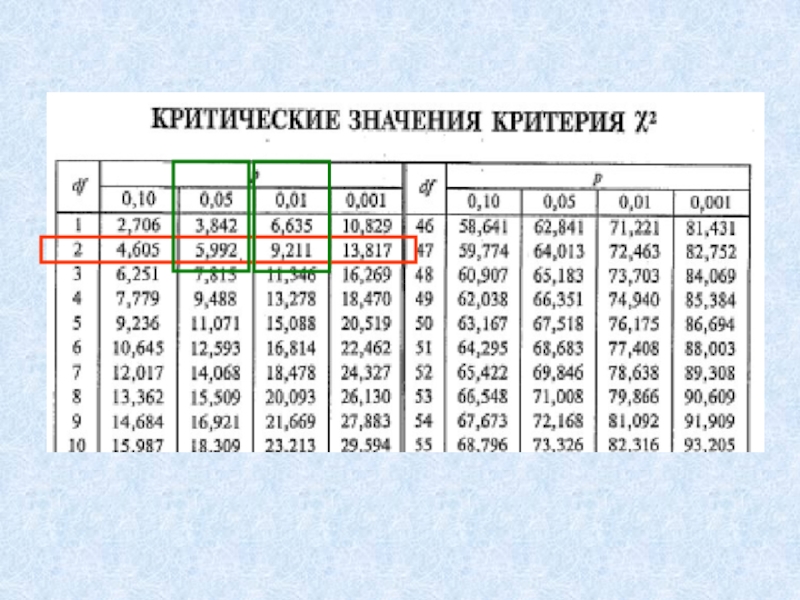
Если объем хотя бы одной
выборки больше 5 либо количество выборок больше 3, то пользуются таблицей критических значений χ2 для df=k-1(k – число выборок)
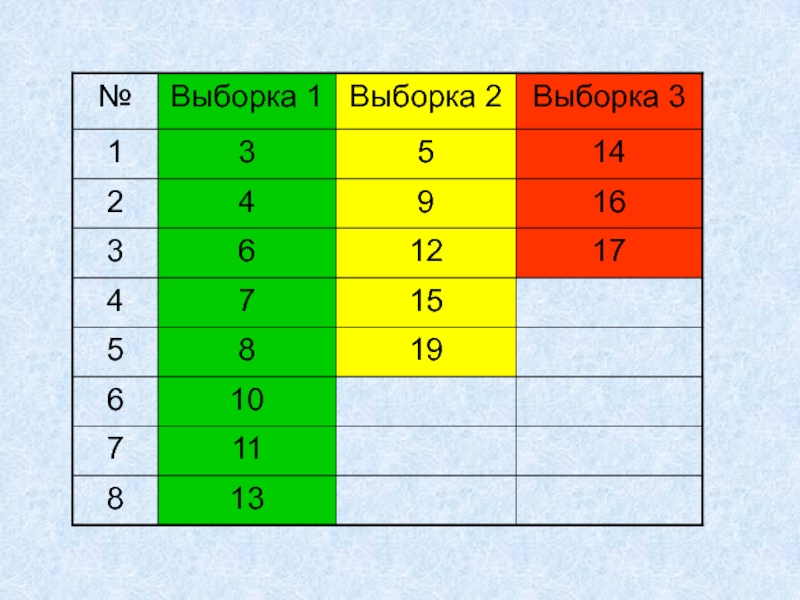
Слайд 91. Значения выборок объединяются в один ряд, упорядоченный в порядке
возрастания или убывания. Обозначается принадлежность каждого значения к той или
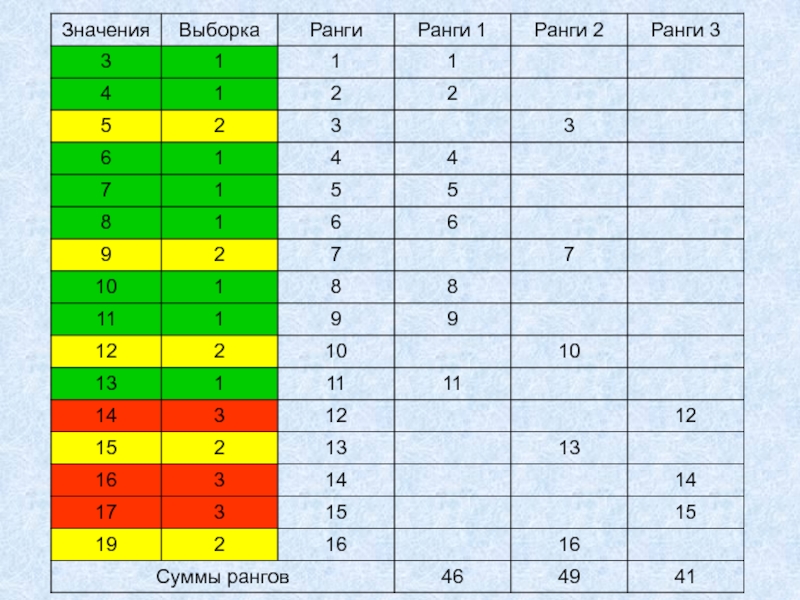
иной выборке.2. Значения выборок ранжируются и выписываются отдельно ранги для каждой выборки.
3. Вычисляются суммы рангов.
Слайд 104. Вычисляется H по формуле.
5. Определяется p-уровень значимости.
6. Принимается статистическое
решение.
H=6,575
Слайд 12зона значимости
зона незначимости
зона неопределенности
p=0,05
p=0,01
5,992
9,211
Подтверждается гипотеза H1.
Имеются значимые различия между выборками
6,575
Слайд 13Сравнение более двух зависимых выборок
Непараметрический критерий χ2-Фридмана (хи-квадрат).
Аналог – однофакторный
дисперсионный анализ ANOVA для повторных измерений.
Слайд 14где
N – число объектов (испытуемых)
k – количество условий (повторных измерений)
Ri
– сумма рангов для условия i
Слайд 15Если k=3, N>9 или k>3, N>4, то пользуются обычной таблицей
для χ2.
Если k=3, N
таблицами критических значений χ2-Фридмана.
Слайд 161. Для каждого объекта условия ранжируются (по строке).
2. Вычисляется
сумма рангов для каждого условия.
3. Вычисляется эмпирическое значение χ2 по
формуле.4. Определяется уровень значимости.
5. Принимается статистическое решение.
Слайд 19зона значимости
зона незначимости
зона неопределенности
p=0,05
p=0,01
7,815
11,346
Подтверждается гипотеза H1.
Имеются значимые различия между выборками
8,6
