Слайд 1ЛЕКЦИЯ 8
8.1.КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
8.2. ТОЧКИ И ЛИНИИ НА КРИВЫХ ПОВЕРХНОСТЯХ
8.3. ПЕРЕСЕЧЕНИЕ
КРИВЫХ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ
8.4. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С КРИВОЙ ПОВЕРХНОСТЬЮ
8.5. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ
ПОВЕРХНОСТЕЙ
Начертательная геометрия
Слайд 28.1. Классификация поверхностей
Кривая поверхность – это совокупность всех
положений некоторой линии движущейся в пространстве.
Движущаяся линия
называется образующей поверхности, а линии, определяющие закон её перемещения, направляющими.
Образующая может быть кривой и прямой.
Поверхность, образуемая движением прямой линии, называется линейчатой, а движением криволинейной образующей – нелинейчатой поверхностью.
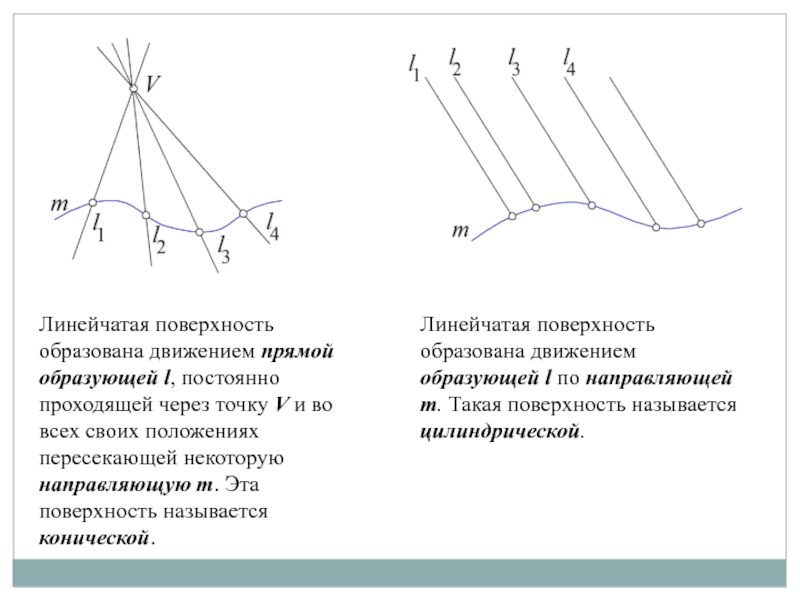
Слайд 3Линейчатая поверхность образована движением прямой образующей l, постоянно проходящей через
точку V и во всех своих положениях пересекающей некоторую направляющую
m. Эта поверхность называется конической.
Линейчатая поверхность образована движением образующей l по направляющей m. Такая поверхность называется цилиндрической.
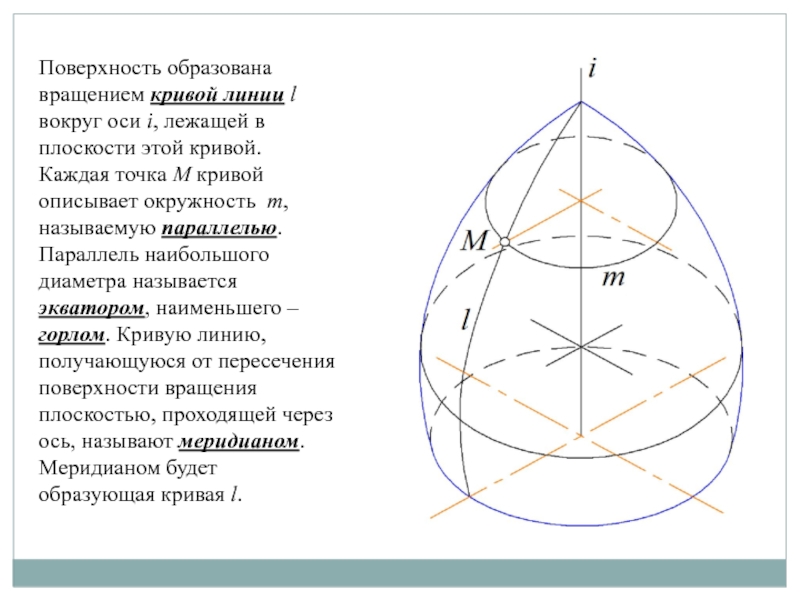
Слайд 4Поверхность образована вращением кривой линии l вокруг оси i, лежащей
в плоскости этой кривой. Каждая точка М кривой описывает окружность
m, называемую параллелью. Параллель наибольшого диаметра называется экватором, наименьшего – горлом. Кривую линию, получающуюся от пересечения поверхности вращения плоскостью, проходящей через ось, называют меридианом. Меридианом будет образующая кривая l.
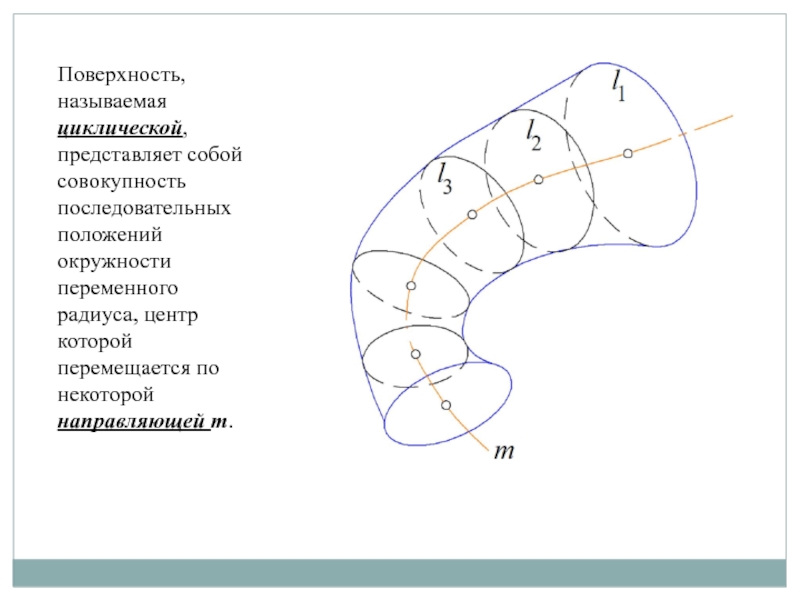
Слайд 5Поверхность, называемая циклической, представляет собой совокупность последовательных положений окружности переменного
радиуса, центр которой перемещается по некоторой направляющей m.
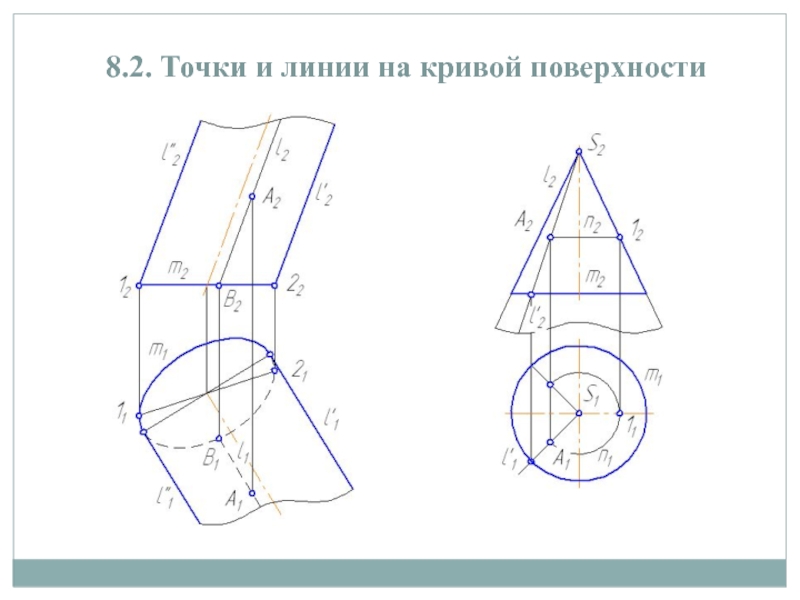
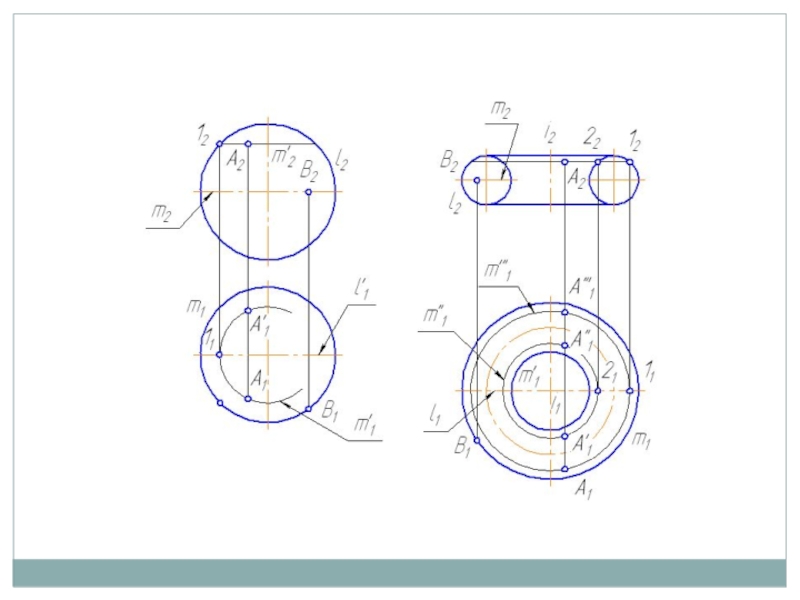
Слайд 68.2. Точки и линии на кривой поверхности
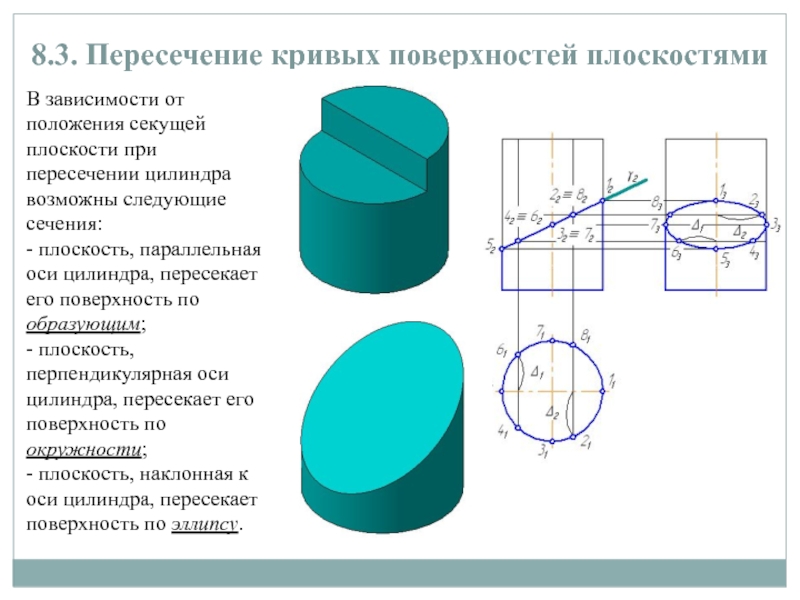
Слайд 88.3. Пересечение кривых поверхностей плоскостями
В зависимости от положения секущей плоскости
при пересечении цилиндра возможны следующие сечения:
- плоскость, параллельная оси цилиндра,
пересекает его поверхность по образующим;
- плоскость, перпендикулярная оси цилиндра, пересекает его поверхность по окружности;
- плоскость, наклонная к оси цилиндра, пересекает поверхность по эллипсу.
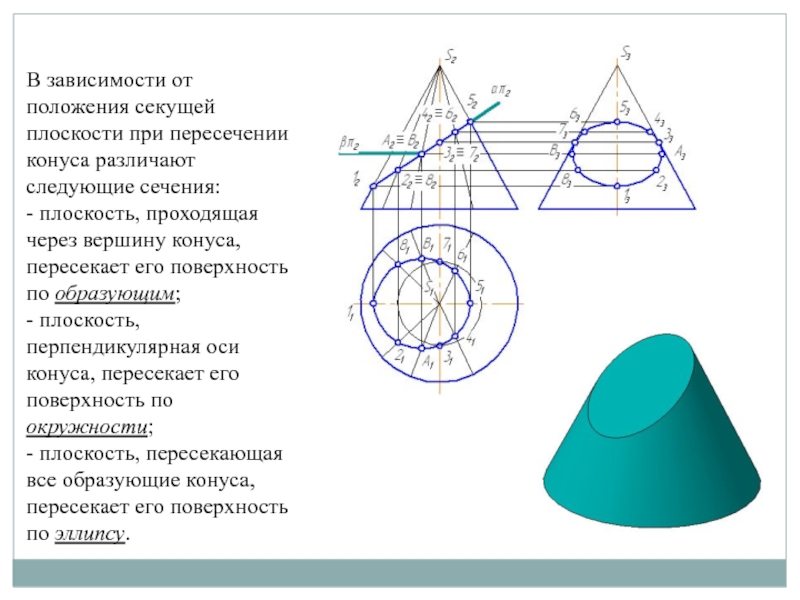
Слайд 9В зависимости от положения секущей плоскости при пересечении конуса различают
следующие сечения:
- плоскость, проходящая через вершину конуса, пересекает его поверхность
по образующим;
- плоскость, перпендикулярная оси конуса, пересекает его поверхность по окружности;
- плоскость, пересекающая все образующие конуса, пересекает его поверхность по эллипсу.
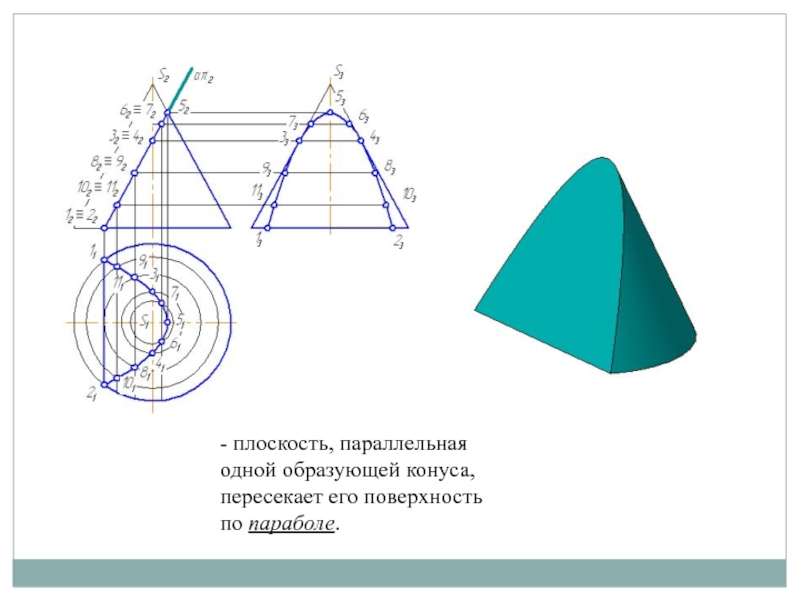
Слайд 10- плоскость, параллельная одной образующей конуса, пересекает его поверхность по
параболе.
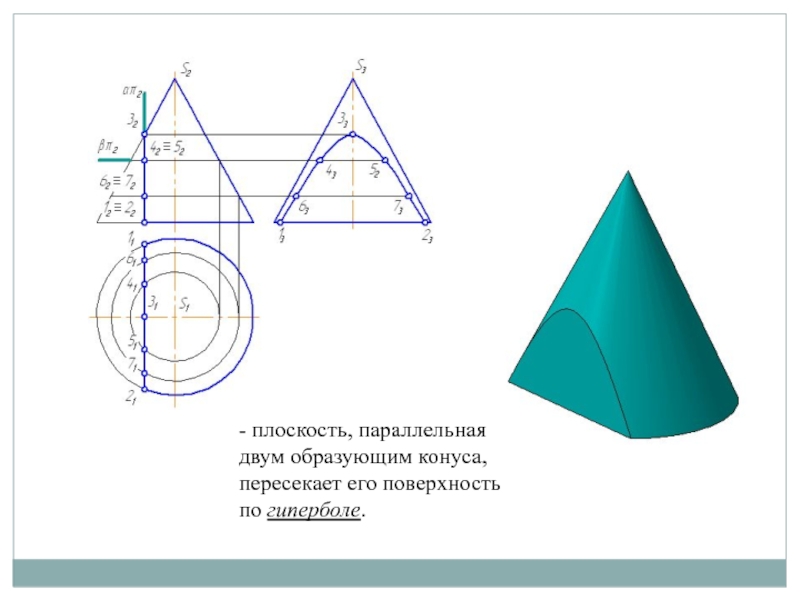
Слайд 11- плоскость, параллельная двум образующим конуса, пересекает его поверхность по
гиперболе.
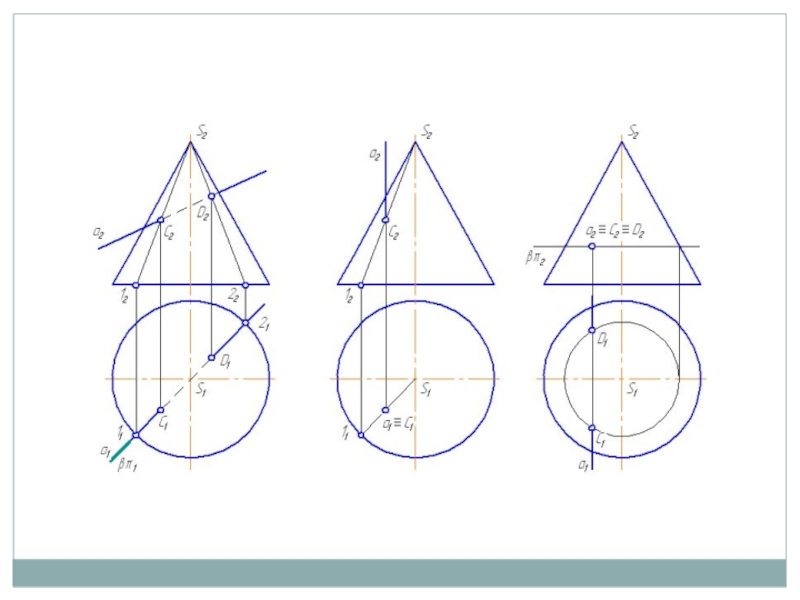
Слайд 138.4. Порядок построения линий пересечения
кривых поверхностей плоскостью общего положения
Для нахождения кривой линии, получаемой при пересечении поверхности
плоскостью общего положения, следует:
провести несколько вспомогательных плоскостей, пересекающих одновременно данную кривую поверхность и секущую плоскость. При этом вспомогательные плоскости выбирают так, чтобы они пересекали кривую поверхность по наиболее простым для построения линиям (прямым или окружностям);
построить линии, по которым вспомогательные плоскости пересекают данную поверхность и секущую плоскость;
найти точки, в которых построенные линии пересекаются между собой;
соединить найденные точки в правильной последовательности.
В первую очередь следует определять так называемые характерные (иначе опорные) точки фигуры сечения и только после нахождения таковых построить еще несколько дополнительных точек в тех местах, где очерк фигуры сечения определен недостаточно полно.
Характерными точками фигуры сечения будут точки, лежащие на очерковых образующих проекций поверхности, высшая и низшая точки, ближайшая к фронтальной плоскости проекций и наиболее удаленная от нее.

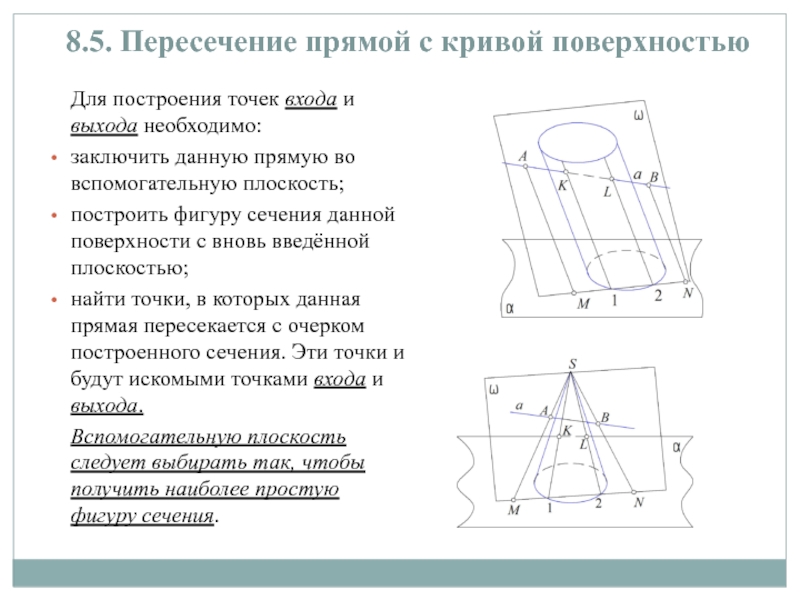
Слайд 158.5. Пересечение прямой с кривой поверхностью
Для построения точек
входа и выхода необходимо:
заключить данную прямую во вспомогательную плоскость;
построить фигуру
сечения данной поверхности с вновь введённой плоскостью;
найти точки, в которых данная прямая пересекается с очерком построенного сечения. Эти точки и будут искомыми точками входа и выхода.
Вспомогательную плоскость следует выбирать так, чтобы получить наиболее простую фигуру сечения.
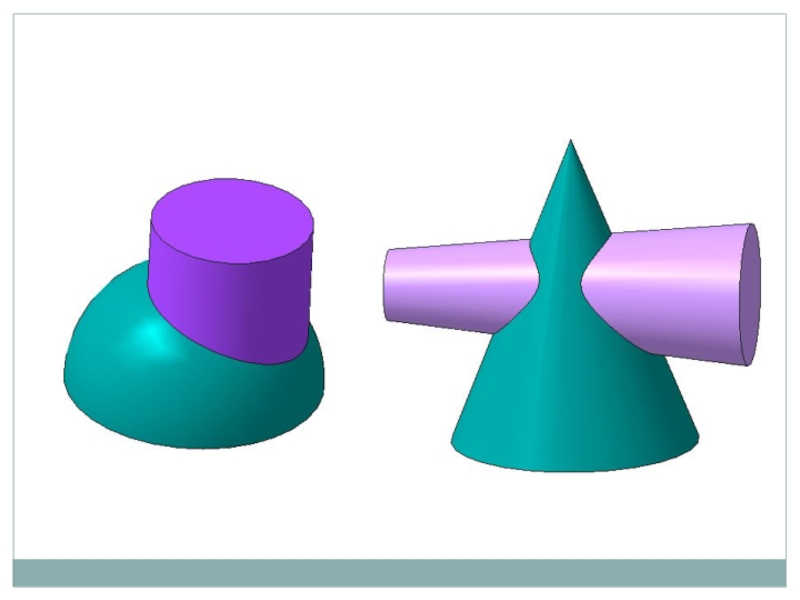
Слайд 178.6. Взаимное пересечение поверхностей
8.6.1. Метод секущих плоскостей
Порядок построения линии пересечения
поверхностей:
- ввести несколько вспомогательных плоскостей (поверхностей), пересекающих заданные поверхности;
- построить
линии, по которым вспомогательные плоскости (поверхности) пересекают каждую из заданных поверхностей;
- найти точки, в которых построенные линии пересекаются между собою;
- соединить найденные точки в правильной последовательности и получить линию, по которой данные поверхности пересекаются между собою.
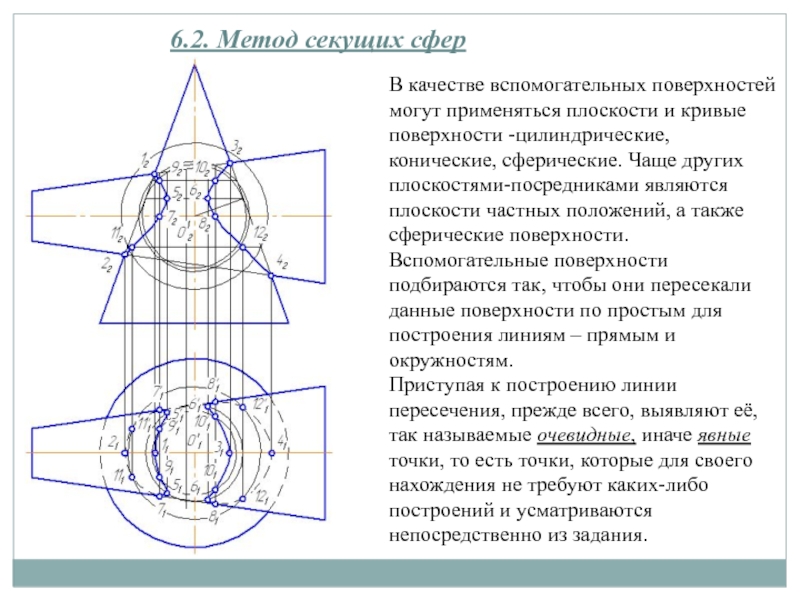
Слайд 186.2. Метод секущих сфер
В качестве вспомогательных поверхностей могут применяться плоскости
и кривые поверхности -цилиндрические, конические, сферические. Чаще других плоскостями-посредниками являются
плоскости частных положений, а также сферические поверхности.
Вспомогательные поверхности подбираются так, чтобы они пересекали данные поверхности по простым для построения линиям – прямым и окружностям.
Приступая к построению линии пересечения, прежде всего, выявляют её, так называемые очевидные, иначе явные точки, то есть точки, которые для своего нахождения не требуют каких-либо построений и усматриваются непосредственно из задания.