Кривые второго порядка

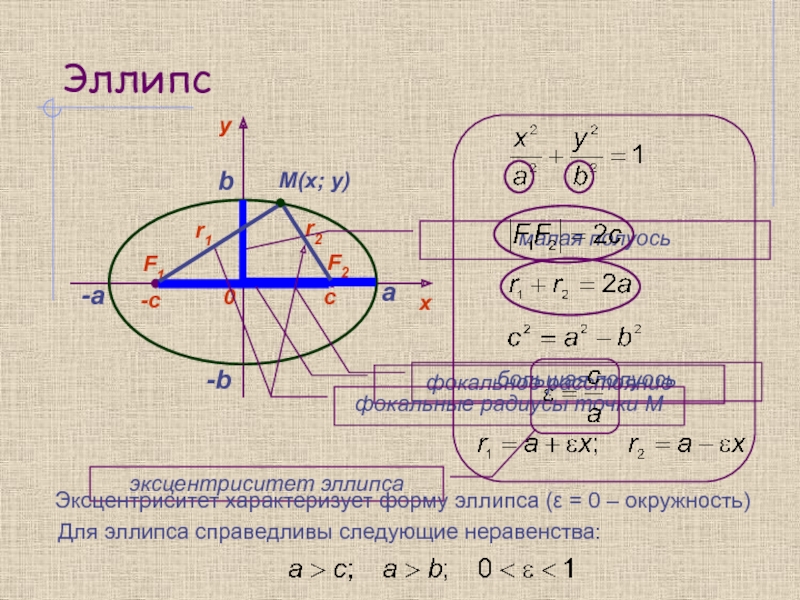
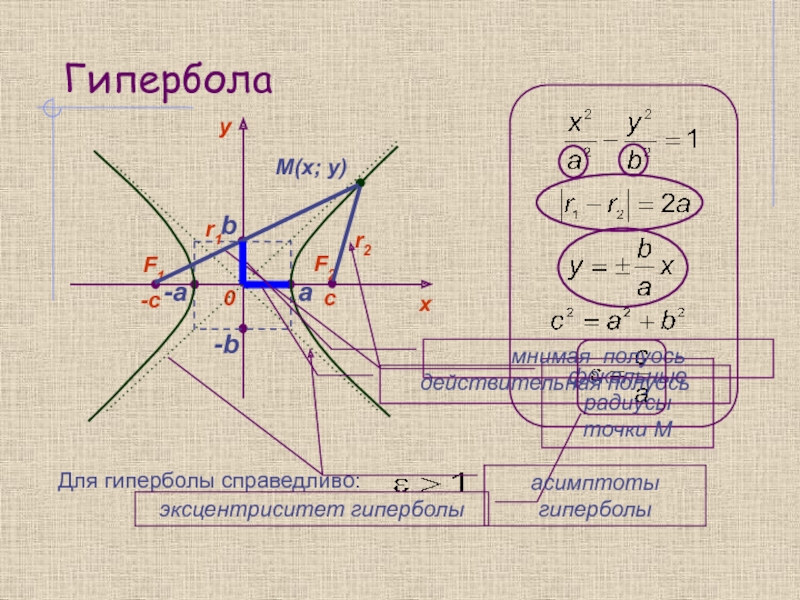
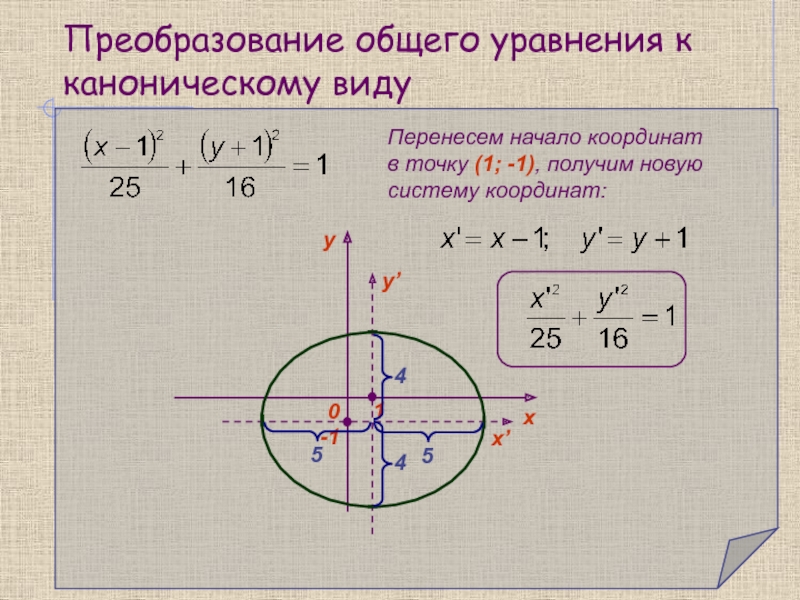
частным случаем которого является окружность, гипербола и парабола.
Они задаются уравнением

Общее уравнение кривой второго порядка

В некоторых частных случаях это уравнение может определять также две прямые, точку или мнимое геометрическое место.

А(a; b) на расстояние R.
А
R
М(x; y)
Для любой точки М

Каноническое уравнение окружности

которых до двух точек той же плоскости F1 и F2,

F1

F2

-c

c

M(x; y)

r1

r2

Зададим систему координат и начало координат выберем в середине отрезка [F1 F2]

0 – окружность)

F2(4; 0), а эксцентриситет равен 0,8.
Каноническое уравнение эллипса:
-5
5
-3
3

которых до двух точек той же плоскости F1 и F2,

F1

F2

-c

c

M(x; y)

r1

r2

асимптоты заданы уравнениями:
Решим систему:
Точка А лежит на гиперболе

определителя:
Дискриминант старших членов уравнения
Дискриминант уравнения

если 2Bxy=0:
Приведение пяти-членного уравнения к каноническому виду рассмотрим на примере:

(1; -1), получим новую систему координат:

уравнении не равно нулю, то для приведения уравнения к каноническому

Угол α удовлетворяет условию:

В случае, если A = C, то