КВАНТОВАЯ ТЕОРИЯ АТОМА ВОДОРОДА E. Schredinger. Ann. Phisik, 1926, 79, 361

Квантование как задача о собственных значениях. Первое сообщение.
E. Schredinger. Ann.

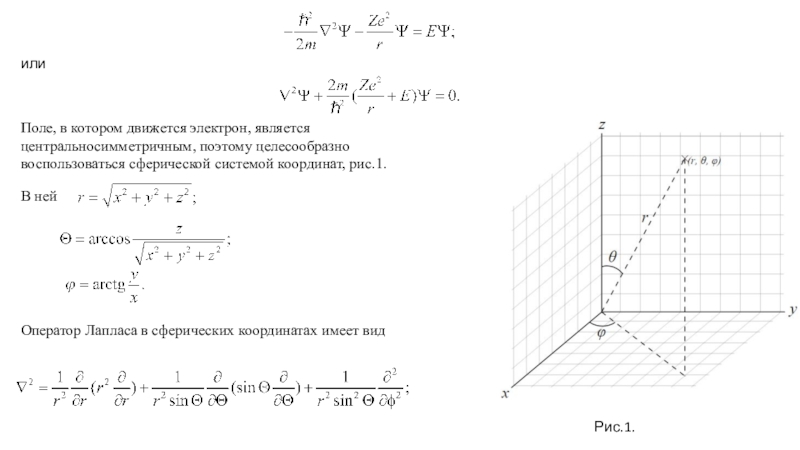
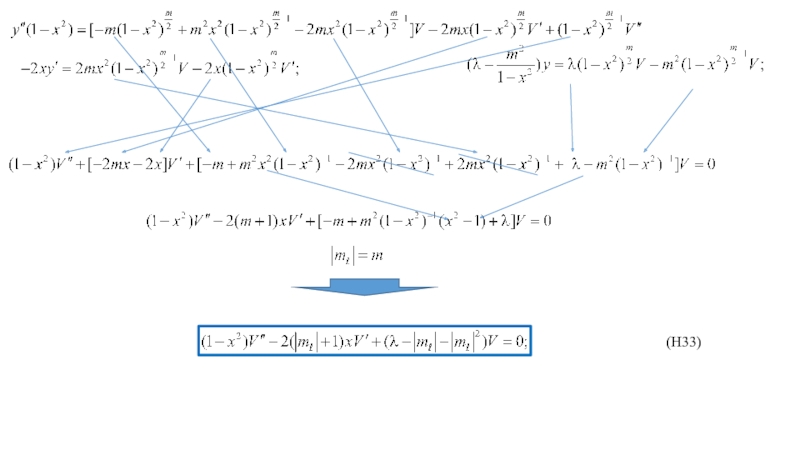
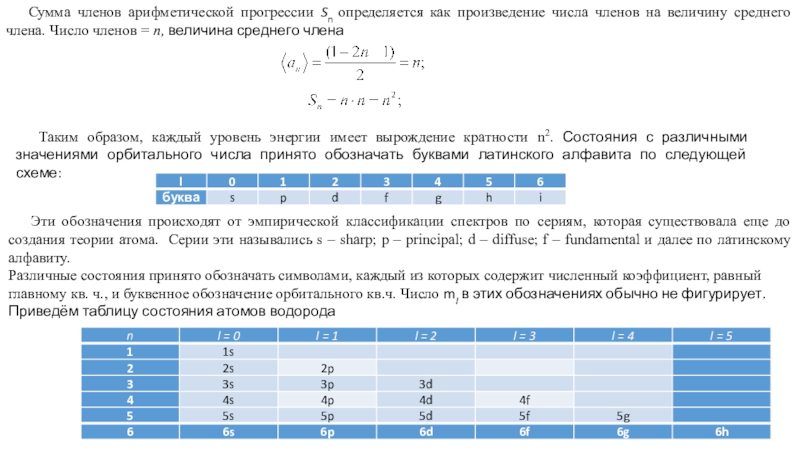
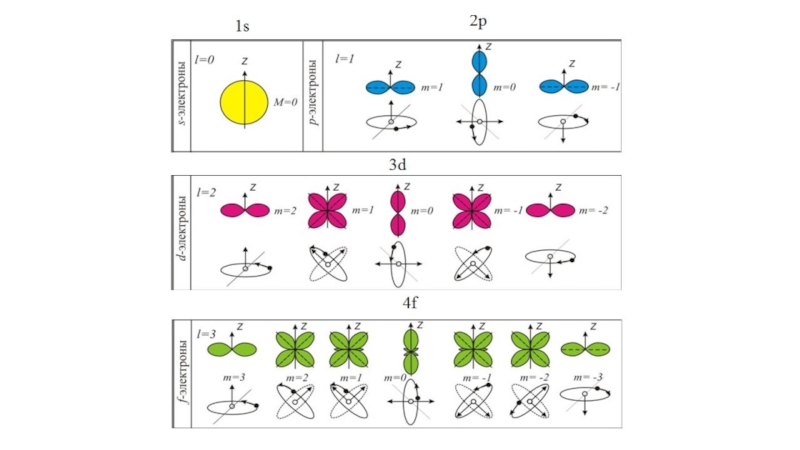
Phisik, 1926, 79,489. Квантование как задача о собственных значениях. Второе сообщение*.

Из многочисленных работ, вышедших из под пера Эрвина Шредингера, выделяются две, ссылки на которые приведены выше, в которых он сформулировал основные положения, как он говорил, волновой механики, получил волновое уравнение – уравнение Шредингера, и применил их в частности к решению задачи на отыскание стационарных уровней энергии в атоме водорода и распределении плотности вероятности для электрона в этих состояниях.
В этих же работах именно он сформулировал стандартные условия, о которых мы уже говорили ранее при решении задачи о движении частицы в потенциальной яме с бесконечно высокими стенками: именно, требования конечности и непрерывности волновой функции вместе с её первой производной, а также условие нормировки волновых функций.
Сам он писал: «В этом сообщении я собираюсь показать, на простейшем примере нерелятивистского свободного атома водорода, что обычные правила квантования могут быть заменены другими положениями, в которых уже не вводится каких-либо целых чисел. Целочисленность при этом получается единственным образом сама по себе подобно тому как сама по себе получается целочисленность числа узлов при рассмотрении колеблющейся струны. Это новое представление может быть обобщено, и я думаю, что оно тесно связано с истинной природой квантования».

мире. Наряду с коренной ломкой взглядов на атомные явления, эта

теория позволила понять такие близкие проблемы как характер взаимодействия атомов при образовании стабильных молекул, происхождение периодической системы элементов и наличие характерных электрических, магнитных, механических и оптических свойств у твёрдых тел. Однако первым продуктивным шагом на этом пути было решение задачи водорода. В упомянутых выше работах многие математические детали опущены, что оправдано в научной публикации. Мы же с целью изучения предмета воспроизведем решение во всей его полноте.
Атом водорода состоит из протона, электрический заряд которого +e, в котором сосредоточена практически вся масса атома, и электрона – частицы с массой в 1836 раз меньшей и зарядом –e, который удерживается вблизи протона электрическим полем. В первом приближении при таком соотношении масс можно полагать ядро совершенно неподвижным, однако, если потребуется учесть его движение, то это легко сделать, как делалось в теории Бора, путём замены массы электрона m на приведённую массу µ=mM/(m+M).
Идеологически совершенно всё равно, каков заряд ядра, поэтому мы будем решать задачу сразу не только для собственно атома водорода с одним электроном вокруг него, но также и для так называемых водородоподобных атомов – систем с зарядом ядра ze и движущегося вокруг него электрона. При этом Z полагается целым. В частности при Z = 1 получаем атом водорода.
Потенциальная энергия электрона в таком атоме равна

r – расстояние между неподвижным точечным ядром, расположенным в начале отсчета, и электроном.
Общий вид уравнения Шредингера для стационарных состояний

Или

системой координат, рис.1.
Рис.1.
В ней
Оператор Лапласа в сферических координатах имеет

вид

для волновой функции электрона в атоме водорода. Вместе со стандартными

условиями, накладываемыми на волновую функцию и её производную оно однозначно определяет поведение электрона в данной системе.

(Н6)

Преимущество записи уравнения в сферических координатах при решении задачи об атоме водорода заключается в том, что в таком виде его легко разделить на три уравнения, каждое из которых зависит только от одной координаты. Попытаемся найти решение уравнения (Н6) в виде произведения трёх различных функций:

зависящей только от r;

зависящей только от и

зависящей только от ,

То есть предположим, что решение имеет вид

Функция R(r)

характеризует изменение волновой функции электрона вдоль радиус-вектора при постоянных и .

Функция описывает изменение  в зависимости от угла вдоль меридиана на сфере, центром которой служит
ядро, при постоянных r и .

Функция характеризует изменение  в зависимости от азимутального угла  вдоль параллели на сфере, центром которой служит ядро, при постоянных r и .

(Н7)

Разделение переменных

не будет: =RTФ.
Подставив (Н7) в уравнение (Н6), получаем:
Вынося функции,

не зависящие от переменных по которым производится дифференцирование, получаем

Разделим уравнение на RTФ, и умножим на

Перепишем его в виде

Левая часть зависит от r и

а правая – только от

И, тем не менее, они равны друг другу. Очевидно, что это может быть только в том случае, если левая и правая часть равны одной и той же константе. Эту постоянную удобно обозначить как . Таким образом, имеем два уравнения:

справа – от .
Снова получаем уравнение, справа и

слева в котором стоят функции разных переменных. Это значит, что каждая из сторон должна равняться одной и той же постоянной. Обозначим её λ.

Таким образом, имеем три уравнения:

;

(Н11)

функции, зависящей от одной переменной. Следовательно, мы можем заменить символы

частных производных на символы полных производных. Полученное нами упрощение весьма существенно. Перепишем эти уравнения в символах прямых дифференциалов, а кроме того, первое умножим на R, второе на Т, третье на Ф.

Мы получили три независимых уравнения на собственные значения для соответствующих дифференциальных операторов. Решение последнего из уравнений общеизвестно:

В силу требования однозначности, функция должна быть периодической с периодом 2. То есть должно выполняться равенство

так как физически 2+ есть тот же угол, что и . Такая периодичность будет иметь место, если параметр равен любому целому числу, включая ноль:

Решение угловой части

 d = -dx/sin, sin2 = 1 – x2.

(H19)
Обозначим

. Область определения x  [-1,+1].

Дифференцируем первую скобку

Так как входит в квадрате, y может быть функцией только .

Будем искать y в виде:

(Н25)

(Н27)

(Н26)

Для того, чтобы получить первый член в (Н25), умножим левую

и правую часть на

Для того, чтобы получить второй член в (Н25), умножим левую и правую часть (Н27) на -2x

Подставим выбранный вид решения (Н26) в третий член уравнения (Н25)

Подставим три последних выражения (*, **,***)в уравнение (Н25) . Учтем, что все члены пропорциональны ,

поэтому сократим на . Соберем члены с соответствующими порядками производных функции V.

*

**

***

нулю, если коэффициенты при всех степенях x будут равны нулю.
Если

взять степень равную  в первом члене

то во всех остальных степень  достигается при ν = . Таким образом номер члена, а соответственно и номер
коэффициента “a” в первом члене на два больше чем во всех остальных.

Приравниваем нулю коэффициент при и опять обозначая , получаем

(Н34)

(Н33)

наше решение

было конечным, непрерывным и однозначным, необходимо,

чтобы сумма содержала конечное число членов – была многочленом.

или при

Обозначив получаем

а так как сумма по ν берется по целым положительным числам и

Кроме того, введенные при интегрировании уравнений константы λ и оказываются связанными.

(H45)

с aν+2 (в силу (Н41)) будут равны нулю.
Это первое

условие, а второе состоит в том, что сумма должна содержать только члены одинаковой чётности.

Решение

принадлежащее характеристическим числам

и

обозначим через

Ограничение на

следует из (Н45), так как >0.

где при m=0

называется полиномом Лежандра порядка l.

Коэффициент при нём обычно нормирован так, что

- присоединённый полином Лежандра.

Полином Лежандра может быть представлен формулой

Таким образом, окончательный вид решения уравнения для функции

где Nlm - нормированный множитель.

называются сферическими и представляют собой угловую часть семейства ортогональных

решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией.

Они образуют ортонормированную систему в пространстве функций на двумерной сфере, то есть применительно к нашей задаче при r = const. Ортонормированность означает выполнение равенств

где

Совокупность сферических функций для данного уравнения Лапласа обладает свойством полноты, то есть Любая функция , имеющая непре­рывные вторые производные, может быть равномерно аппро­ксимирована некоторым полиномом из сферических функций.

волновой функции.
Подставляя допустимые значения

получаем

(H56)

Умножим (H56) на

и приведем к стандартному виду уравнения Шредингера,

Это - уравнение, отвечающее движению в одном измерении с некоторой эффективной потенциальной энергией

В аналитической механике при рассмотрении движения в центральном поле для эффективной потенциальной энергии получается выражение

(H57)

(H57’)

атоме водорода квантуется, причем
Полученное выражение отличается от боровского условия квантования

круговых орбит, согласно которому и нет ограничений на n.

Рассмотрим, как ведет себя эффективная потенциальная энергия (H57). Графики знаменателей даны на рис.1. При малых значениях аргумента преобладает линейная функция, при больших – квадратичная. Соответственно, при малых r преобладает , - потенциальная энергия положительна и резко растет с уменьшением радиуса, при больших преобладает , - потенциальная энергия отрицательна и с ростом радиуса стремится к нулю, рис.2.
Нас интересуют связанные состояния электрона, то есть такие, когда он находится в потенциальной яме, поэтому будем рассматривать только случай .

Рис.1

рис.2.

Поскольку во всех уравнениях складываются члены одинаковой размерности, размерность равняется (длина)-2 , поэтому можно принять

Кроме того, обозначим , тогда (H56) приобретет вид

(H56)

можно пренебречь всеми членами, содержащими r

в знаменателе и рассматривать уравнение

Его частные решения имеют вид , а общее решения является их линейной комбинацией:

В соответствии со стандартными условиями, при должно быть , поэтому В = 0 и общее решение (Н61) имеет вид

Учтя введем безразмерную переменную

Сохраним обозначение для решения, тогда

выраженные через ρ в
(Н60)
(Н60)

виде степенного ряда
Подставляя функцию f(ρ) и её производные в уравнение

(Н72), получаем

(Н72)

(Н73)

Собирая члены, пропорциональные одинаковым степеням ρ, получаем

быть нулю. Во все степени за исключением минимальной дают вклады

обе квадратные скобки, а в минимальную, при ν=0 - только первая. Отсюда, полагая ν=0 в первой скобке, получаем

Для того, чтобы решение было ограниченным , ряд (Н73) должен содержать конечное число членов. Оба корня γ1 и γ2 обеспечивают равенство нулю первой скобки при ν=0, однако вторая не равна нулю и оказывается пропорциональна

Выносим в первых двух членах (ν +γ):

дает неограниченно

возрастающее при ρ 0, для l = 0, 1, в то время как


γ=l дает при ρ 0, если l > 1 и при l = 1.
Итак, корень γ=-(l+1) необходимо отбросить. Теперь уравнение (Н72) перепишем в виде

неограниченно возрастающее при ρ 0, поэтому

его необходимо отбросить. В то время как γ = l дает при если l > 1. Ограниченность решения при обеспечивается за счет обрыва ряда.
Итак, корень γ=-(l+1) необходимо отбросить, теперь при γ = l уравнение (Н74) перепишется в виде

(Н74)

Степень первой скобки на 1 меньше чем степень второй при заданном ν, соответственно одинаковые степени достигаются при значении индекса ν для первой скобки на 1 больше, чем у второй, отсюда

Решение содержит , следовательно, оно будет конечным в случае, если при растет

слабее чем , однако, при больших ν получаем

ведет себя как

, а

(Н73)

т.е. в случае неограниченного числа членов ряда он расходится при , следовательно, если мы хотим
получить ограниченное решение, разложение необходимо оборвать на некотором члене, обозначим его номер

Шредингера.
Как видно, энергия En зависит от одного квантового числа, называемого

главным квантовым числом. Оно является суммой двух квантовых чисел – радиального nr и азимутального l (или орбитального) плюс единица:

n = nr+l+1

(Н87)

к. l = v +ml .
Наибольшее из l =

n - nr -1 соответствует случаю nr = 0 и равно, следовательно, l = n - 1. Итак, возможные значения квантового числа l при заданным значении n следующие:

l = 0, 1, 2, …, (n - 1).

Различные состояния водородоподобного атома могут быть описаны при помощи трех квантовых чисел: nr, l, ml .

Однако, т. к. задание n и l определяет и nr , то можно, – и это удобнее – характеризовать состояние квантовыми числами n, l, ml (каждое из своего уравнения).

l носит название «орбитальное квантовое число» а ml - «магнитное квантовое число».

Введём понятие вырожденного состояния. Состояние называется энергетически вырожденным, если одному значению энергии соответствует не одно, а несколько состояний, т.е. несколько волновых функций, с различными значениями квантовых чисел.
В общем случае вырождение заключается в том, что некоторая величина L, характеризующая данную систему, имеет одинаковое значение для различных состояний системы. Число таких состояний, которым отвечает одно и тоже значение L называется КРАТНОСТЬЮ ВЫРОЖДЕНИЯ данной величины.
В нашем случае мы имеем дело с вырождением по энергии. Действительно, согласно энергия зависит только от одного квантового числа - n, в то время как их имеется три. Исключение составляет только состояние с n = 1. В этом случае l и ml определяется однозначно, то и другое равны нулю. Следовательно в этом состоянии вырождения по энергии нет. Этого нельзя сказать про остальные состояния. При заданном n, определяющем энергию атома, l может иметь n значений 0, 1, 2, … , (n - 1), но каждому l соответствует ещё (2l + 1) значений ml . Отсюда следует, что для одного определенного значения n, т.е. для каждого значения энергии, определяемого формулой имеется столько различных собственных функций, какова величина суммы:

(Н87)

(Н87)

на величину среднего члена. Число членов = n, величина среднего

члена

Таким образом, каждый уровень энергии имеет вырождение кратности n2. Состояния с различными значениями орбитального числа принято обозначать буквами латинского алфавита по следующей схеме:

Эти обозначения происходят от эмпирической классификации спектров по сериям, которая существовала еще до создания теории атома. Серии эти назывались s – sharp; p – principal; d – diffuse; f – fundamental и далее по латинскому алфавиту.
Различные состояния принято обозначать символами, каждый из которых содержит численный коэффициент, равный главному кв. ч., и буквенное обозначение орбитального кв.ч. Число ml в этих обозначениях обычно не фигурирует. Приведём таблицу состояния атомов водорода

ними отмечают не только квантовые числа, но и располагают уровни

в соответствии с их энергией, тогда получается следующая картина: (учтено что разрешены переходы с изменением орбитального квантового числа на единицу) Δl = ±1.

Правило отбора по орбитальному квантовому числу обусловлено тем, что фотон обладает собственным моментом импульса, равным . При испускании фотон уносит от атома этот момент, а при поглощении привносит. Так что правило отбора есть просто запись закона сохранения момента импульса.

Приведем явные выражения некоторых волновых функций, а также ход радиальной составляющей плотности вероятности.

симметрии волновых функций.
Отсутствие множителя, пропорционального σ – свидетельствует о том,

что плотность вероятности нахождения электрона в центре координат, т.е. на ядре в s – состоянии отлична от нуля (что физический возможно вследствие = 0 момента импульса).
Если вычислить максимумы плотности вероятности для решений уравнения Шредингера, то получается следующие значения:

Согласно теории Бора для радиусов круговых орбит

Приведенный выше ряд максимумов плотности вероятности в точности повторяет
радиусы орбит найденные Бором. Однако соответствие это «размытое» – в последовательной квантовой теории существует отличная от нуля вероятность нахождения электрона не только на указанных расстояниях от ядра. Кроме того часть орбит имеет весьма причудливую форму. Приведем некоторые из них

Probability densities through the xz-plane
for the electron at different quantum numbers
(ℓ, across top; n, down side; m = 0)