в проходящем свете, то последовательность чередования полос изменяется на обратную:
соответствующий Imin в отраженном свете становится Imax в проходящем свете. 2. При освещении пластинки белым светом получается окрашенная интерференционная картина (для некоторых λi выполняются условия максимумов, а для других λi+1 – условия минимумов).
Определим условия, при которых отраженные волны будут когерентными и, следовательно, будут интерферировать, т.е. на практике для них выполняются соотношения:
lког ≥ 2.∆ и hког ≥ 2.d (6)
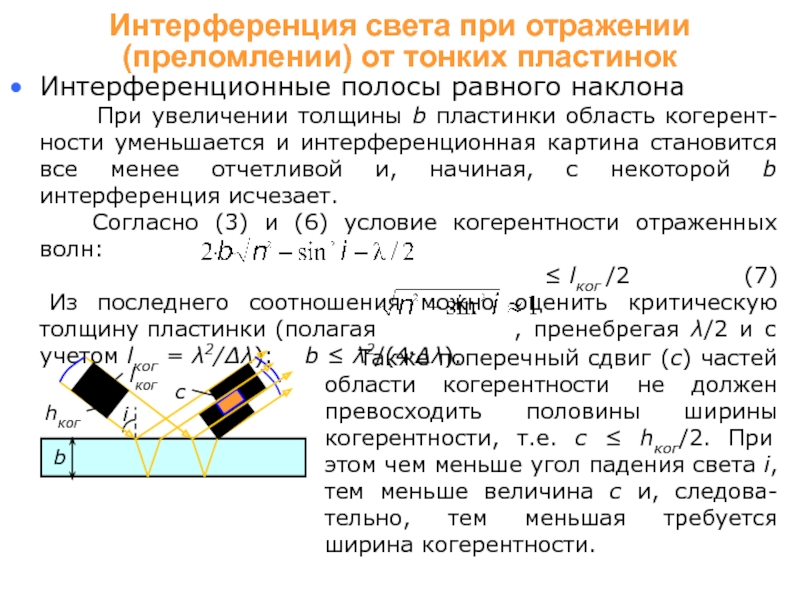
Рассмотрим область когерентности (lког.hког) в падающей волне (на рис. заштрихована) и проследим за ее динамикой.
После «расщепления» падающей волны расщепится и область когерен-тности, причем так, что в отраженных волнах эти области сместятся относи-тельно друг друга. Если при этом они
Интерференция света при отражении (преломлении) от тонких пластинок
lког
hког
перекрываются, то будет наблюдаться интерференция, и тем отчетливее, чем больше степень перекрытия.