Слайд 1Лекция 16
Построение нелинейных решающих функций
Слайд 2Иногда точки обучающей выборки невозможно разделить, используя линейные функции. В
случае, если классы невозможно разделить линейно, используется метод потенциалов, предназначенный
для построения нелинейных решающих функций.
На рисунке приведен пример такого множества, здесь
- элементы первого класса,
- элементы второго класса.
Слайд 3МЕТОД ПОТЕНЦИАЛОВ
В случае, если классы невозможно разделить линейно, используется метод
потенциалов, предназначенный для построения нелинейных решающих функций.
Само название "метод
потенциалов" связано со следующей интерпретацией. Предположим, что любой точке из обучающего множества соответствует некоторый объект, обладающий зарядом (наподобие электрического). Объекты разных классов имеют заряды разных знаков: положительные и отрицательные. В любой точке n-мерного пространства признаков такие заряды создадут некоторый потенциал, являющийся суммой потенциалов отдельных зарядов. Величина потенциала прямо пропорциональна величине заряда и обратно пропорциональна расстоянию до него.
Слайд 4Известно, что линии, соединяющие точки с одинаковыми потенциалами, называются эквипотенциалями.
В таких условиях каждый класс отделен от другого "потенциальной долиной",
имеющей нулевой потенциал. Такая нулевая эквипотенциаль представляет собой границу между классами; ее уравнение и будет решающей функцией.
Функция, описывающая закон изменения потенциала, создаваемого зарядом, помещенным в точку Хс, может быть задана по-разному.
Слайд 5Два варианта расчета
где а>0 – константа (можно принять а=1).
Если
рассматривать расстояние по Евклиду, вторая функция примет вид:
Здесь коэффициент а=1.
Слайд 6Построение решающих правил
Рассмотрим алгоритм построения решающей функции как разделяющей границы
D(X), отделяющей области положительного и отрицательного потенциалов. При описании алгоритма
используем обозначения, принятые в описании алгоритма построения линейной разделяющей функции. Легко заметить, что оба алгоритма имеют много общего.
Рассматривается случай двух классов. Основой для построения D(X) является анализ обучающей выборки Ẋ, где известна заранее принадлежность объектов Ẋ классу 1 или классу 2. Далее эти два класса обозначим С1 и С2. Решающая функция считается построенной, если все объекты обучающей выборки Ẋ распознаются этой функцией правильно, то есть D(X)>0, если Х С1, и, соответственно, D(X)<0, если Х С2
Слайд 7АЛГОРИТМ (1)
Коррекция коэффициентов решающей функции выполняется по следующему правилу: коэффициенты
решающей функции увеличиваются при неправильном распознавании объекта из класса С1,
уменьшаются при неправильном распознавании объекта из класса С2 и остаются без изменения, если распознавание идет правильно.
Слайд 8АЛГОРИТМ (2)
6. Выбрать в качестве текущего класса класс С1.
7. Выбрать
очередной объект Xk из текущего класса . Если текущий класс
исчерпан, объявить текущим класс С2; выбрать из него очередной объект.
8. Построить новую решающую функцию:
9. Если с=0, то сч=сч+1, иначе сч=0.
10. Если сч=М, то КОНЕЦ иначе перейти к шагу 5.
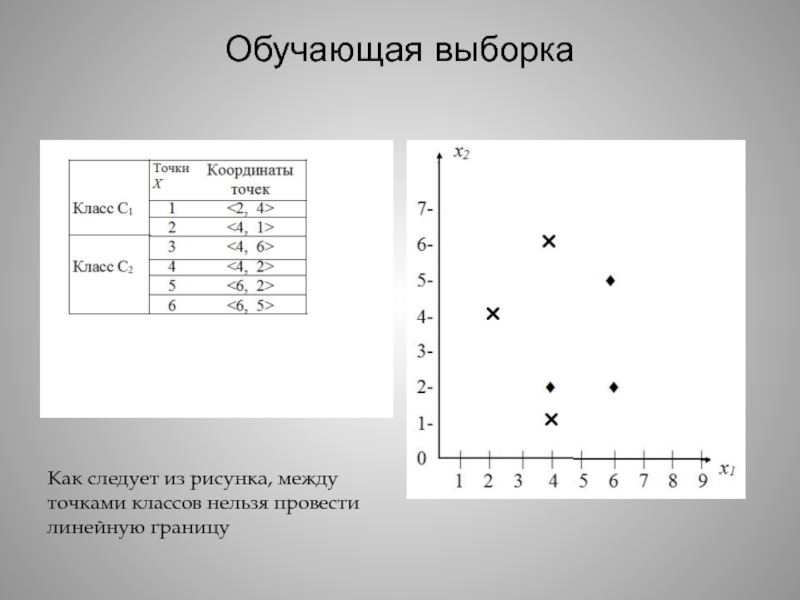
Слайд 9Обучающая выборка
Как следует из рисунка, между точками классов нельзя
провести линейную границу
Слайд 10Пример
Рассмотрим пример работы алгоритма для обучающей выборки, представленной в таблице.
Заметим,
что при выполнении пункта 8 на первой итерации всегда получим
значение множителя с=1, так как
Воспользуемся методом потенциалов, причем для вычисления нелинейной границы предлагается использовать функцию второго типа. Поскольку каждая точка задана двумя координатами, функция примет вид:
Слайд 11Пример (2)
Рассмотрим выполнение алгоритма по шагам.
Слайд 15Результат
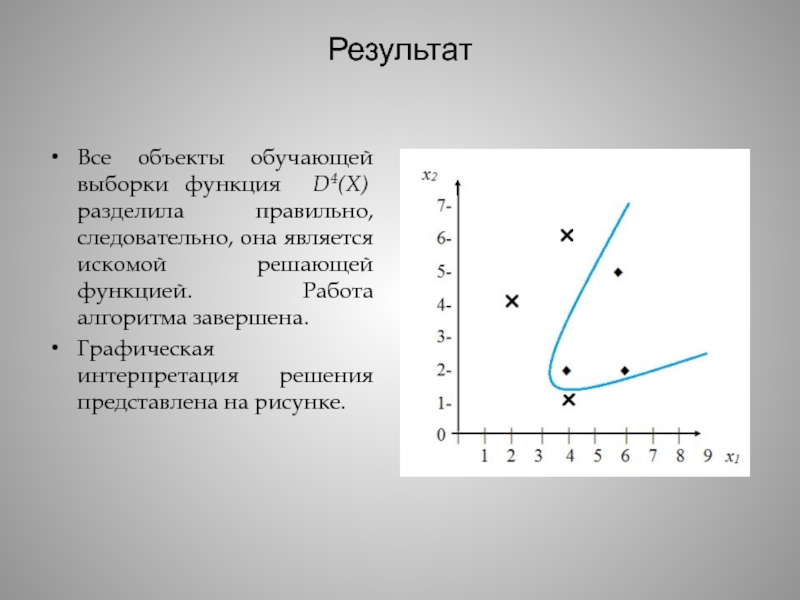
Все объекты обучающей выборки функция D4(X) разделила правильно, следовательно, она
является искомой решающей функцией. Работа алгоритма завершена.
Графическая интерпретация решения представлена
на рисунке.