Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 2
Содержание
- 1. Лекция 2
- 2. План лекции:2.1. Понятие поверхностей второго порядка2.2. Эллипсоид 2.2.1.
- 3. 2.1. Понятие поверхностей второго порядка поверхностей второго
- 4. 2.1. Понятие поверхностей второго порядка поверхностей второго
- 5. 2.2. ЭллипсоидОпределение 1. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид
- 6. Эллипсоид. СвойстваСвойства эллипсоида:1. Эллипсоид – ограниченная поверхность,
- 7. Эллипсоид. Свойства3. Если полуоси попарно различны, то
- 8. 2.2.1. СфераСфера является частным случаем эллипсоида, когда
- 9. Общее уравнение сферыЦентр сферы имеет координаты (a, b, c), где
- 10. Общее уравнение сферы Из общего уравнения сферы можно
- 11. Изображение сферы
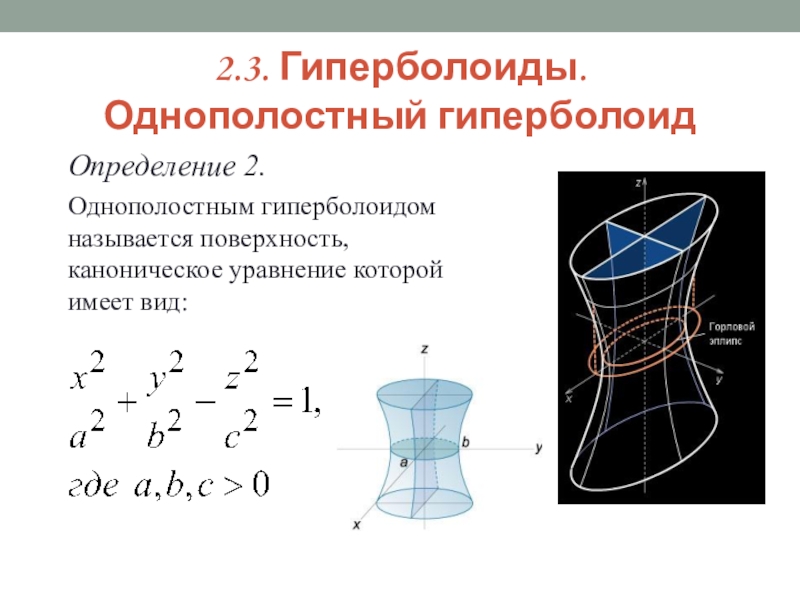
- 12. 2.3. Гиперболоиды. Однополостный гиперболоидОпределение 2. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид:
- 13. Однополостный гиперболоид. СвойстваСвойства однополостного гиперболоида.1. Однополостной гиперболоид
- 14. Однополостный гиперболоид. Свойства3. Если в уравнении однополостного
- 15. 2.3. Гиперболоиды. Двуполостный гиперболоидОпределение 3. Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
- 16. Двуполостный гиперболоид. СвойстваСвойства однополостного гиперболоида.1. Двуполостный гиперболоид
- 17. Двуполостный гиперболоид. Свойства4. Если в уравнении двуполостного
- 18. 2.4. Конические поверхности (конус)Определение 4.Конусом второго порядка
- 19. Конус. СвойстваСвойства конической поверхности1. Точка пересечения конуса
- 20. Виды конических поверхностейМнимая коническая поверхностьКруговая коническая поверхность
- 21. 2.5.1. Эллиптический параболоидОпределение 5. Эллиптическим параболоидом называется
- 22. Эллиптический параболоид. СвойстваСвойства эллиптического параболоида.1. Эллиптический параболоид
- 23. Эллиптический параболоид. Свойства4. Вся поверхность может быть
- 24. 2.5.2. Гиперболический параболоидОпределение 6. Гиперболическим параболоидом называется
- 25. Гиперболический параболоид. СвойстваСвойства гиперболического параболоида.1. Гиперболический параболоид
- 26. Гиперболический параболоид. Свойства5. Вся поверхность может быть
- 27. 2.6. Цилиндрические поверхности Определение 7. Цилиндрической поверхностью называется
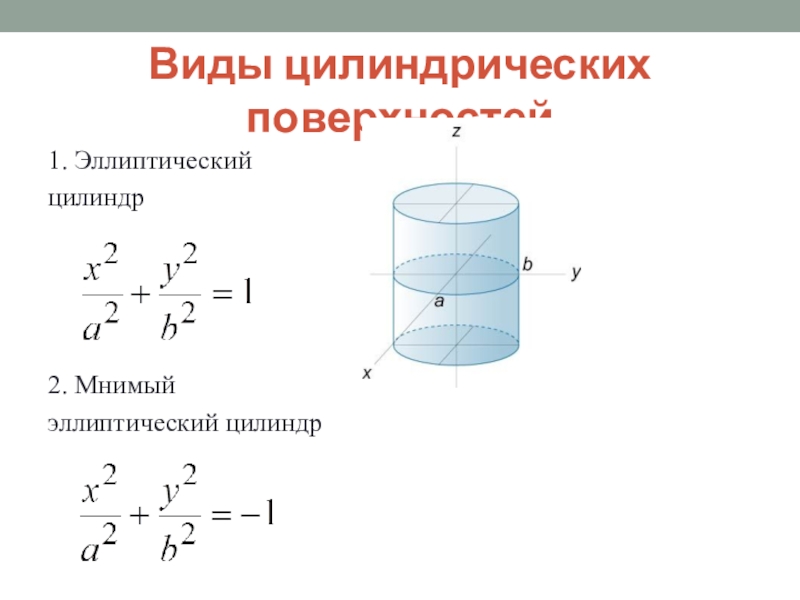
- 28. Виды цилиндрических поверхностей1. Эллиптический цилиндр2. Мнимый эллиптический цилиндр
- 29. Виды цилиндрических поверхностей3. Гиперболический цилиндр4. Параболический цилиндр
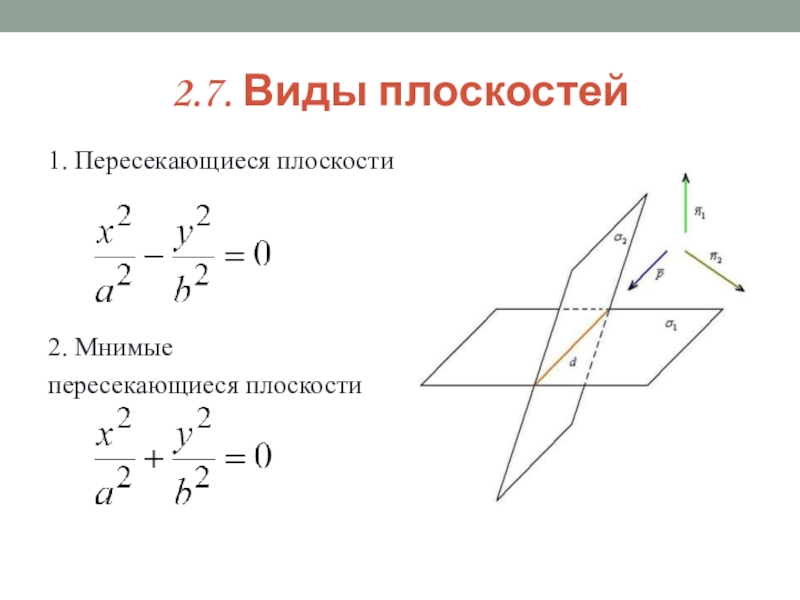
- 30. 2.7. Виды плоскостей1. Пересекающиеся плоскости 2. Мнимые пересекающиеся плоскости
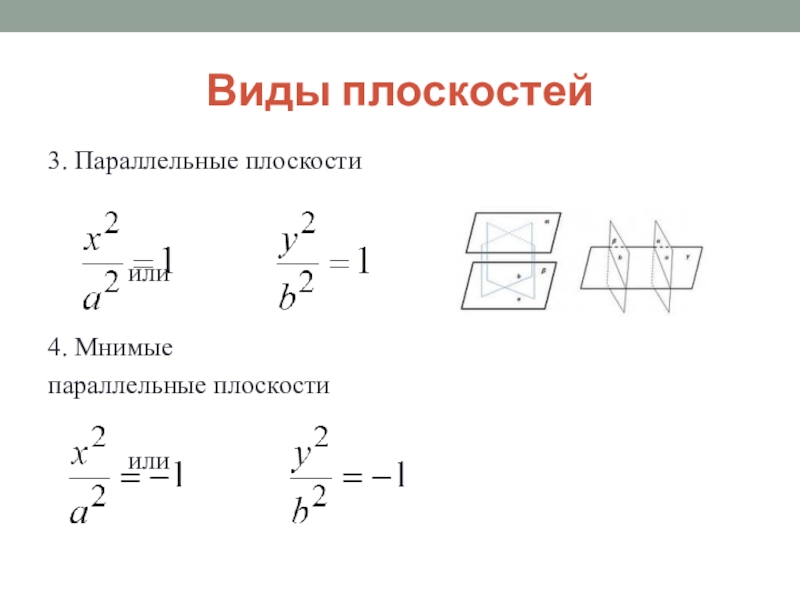
- 31. Виды плоскостей3. Параллельные плоскости или4. Мнимые параллельные плоскости или
- 32. Виды плоскостей5. Совпадающие плоскости или
- 33. 2.8. Классификация поверхностей второго порядкаИсследование вида поверхности
- 34. Классификация поверхностей второго порядка. Основные инварианты
- 35. Классификация поверхностей второго порядка. Основные инвариантыНепосредственной проверкой
- 36. Классификация поверхностей второго порядка. Основные инварианты Поверхность второго
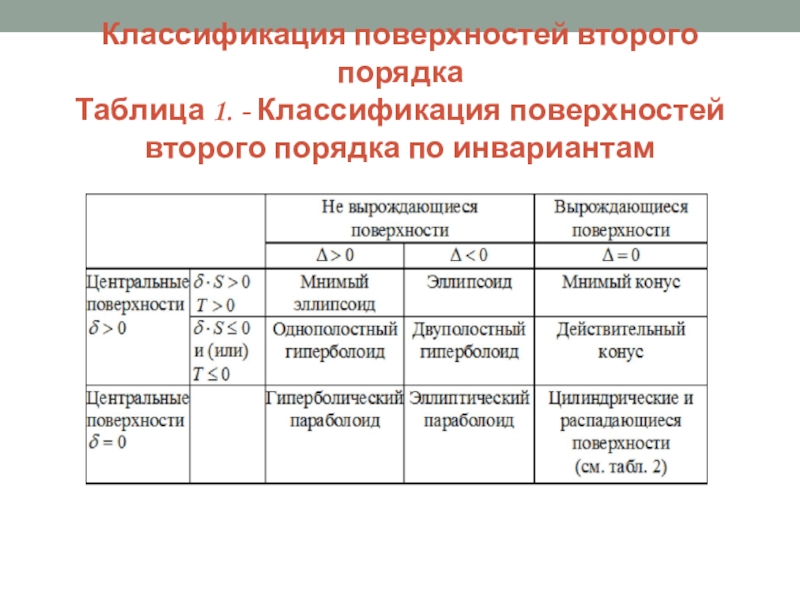
- 37. Классификация поверхностей второго порядка Таблица 1. - Классификация поверхностей второго порядка по инвариантам
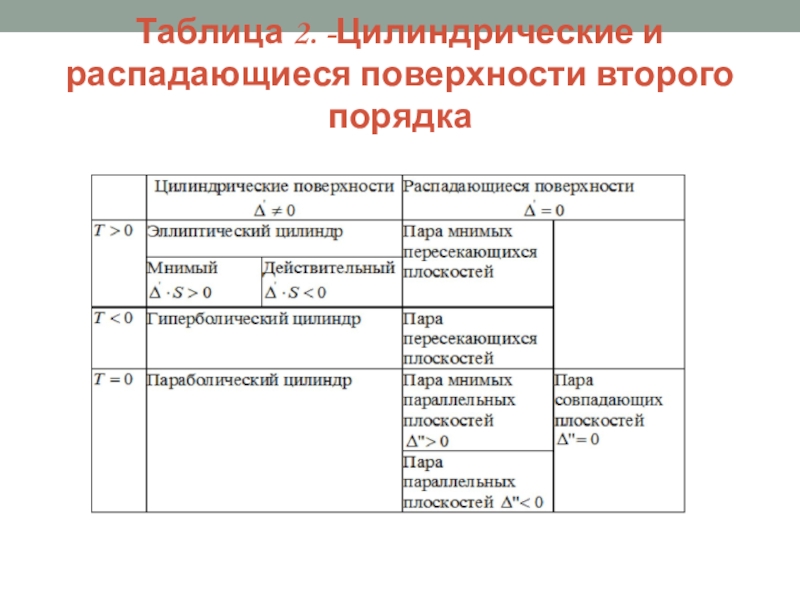
- 38. Таблица 2. -Цилиндрические и распадающиеся поверхности второго порядка
- 39. 2.9. Поверхности второго порядка в сферических координатах Для
- 40. Сферическая система координат
- 41. Сферическая система координат
- 42. Сферическая система координат
- 43. Сферическая система координатСо сферической системой координат можно связать
- 44. Переход от сферических координат к декартовым координатамПриведем формулы связывающие между собой декартовы и сферические координаты:
- 45. Переход от сферических координат к декартовым координатамЭти
- 46. Переход от сферических координат к декартовым координатам
- 47. Пример 1.
- 48. Пример 1. Решение
- 49. Пример 1. Решениеб) Найдем сферические координаты точки
- 50. Пример 1. Решениев) По формулам перехода из декартовой системы координат в сферическую систему координат получим:
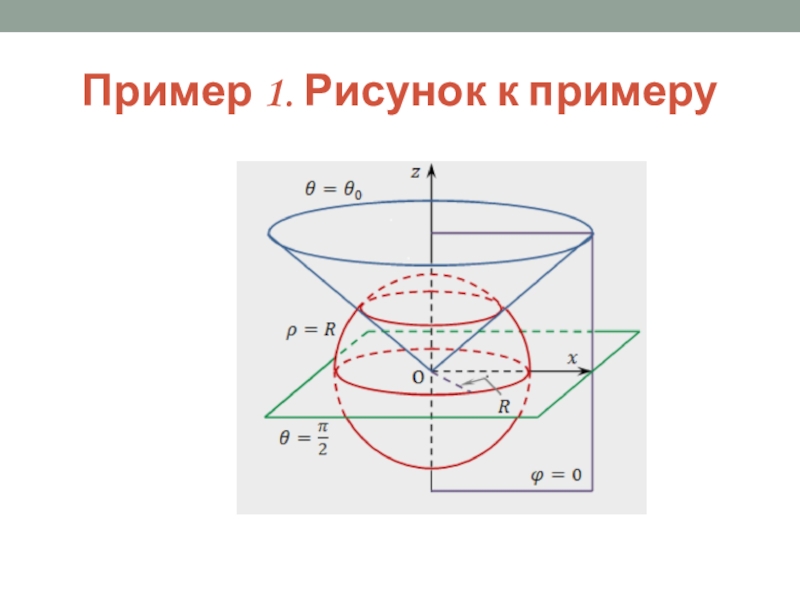
- 51. Пример 1. Рисунок к примеру
- 52. Спасибо за внимание
- 53. Скачать презентанцию
План лекции:2.1. Понятие поверхностей второго порядка2.2. Эллипсоид 2.2.1. Сфера2.3. Гиперболоиды2.4. Конус2.5. Параболоиды2.6. Цилиндры2.7. Плоскости2.8. Классификация поверхностей второго порядка2.9. Поверхности второго порядка в сферических координатах
Слайды и текст этой презентации
Слайд 2План лекции:
2.1. Понятие поверхностей второго порядка
2.2. Эллипсоид
2.2.1. Сфера
2.3. Гиперболоиды
2.4. Конус
2.5.
Параболоиды
в сферических координатах
Слайд 32.1. Понятие поверхностей второго порядка
поверхностей второго порядка
Поверхность второго порядка
геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
(2.1)в котором, по крайней мере, один из коэффициентов
отличен от нуля
Слайд 42.1. Понятие поверхностей второго порядка
поверхностей второго порядка
Уравнение (2.1) мы будем
называть общим уравнением поверхности второго класса порядка. В дальнейшем будет
показано, что поверхности второго порядка, за исключением случаев сильного вырождения, можно разделить на пять типов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.
Слайд 52.2. Эллипсоид
Определение 1. Эллипсоидом называется поверхность, каноническое уравнение которой имеет
вид
Слайд 6Эллипсоид. Свойства
Свойства эллипсоида:
1. Эллипсоид – ограниченная поверхность, поскольку из его
уравнения следует, что
эллипсоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно
координатных осей,плоскостной симметрией относительно начала координат.
2. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Слайд 7Эллипсоид. Свойства
3. Если полуоси попарно различны, то эллипсоид называется трехосным.
4. Если две полуоси равны друг другу, то эллипсоид называется
эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.5. Уравнение мнимого эллипсоида:
Слайд 82.2.1. Сфера
Сфера является частным случаем эллипсоида, когда все его полуоси
одинаковы и равны радиусу сферы.
Уравнение сферы с центром в
начале координат и радиусом R
имеет вид:
Слайд 10Общее уравнение сферы
Из общего уравнения сферы можно найти ее диаметр
по следующей формуле:
Так же можно записать уравнение сферы с центром
в произвольной точке 
Слайд 122.3. Гиперболоиды.
Однополостный гиперболоид
Определение 2.
Однополостным гиперболоидом называется поверхность, каноническое
уравнение которой имеет вид:
Слайд 13Однополостный гиперболоид. Свойства
Свойства однополостного гиперболоида.
1. Однополостной гиперболоид – неограниченная поверхность, поскольку
из его уравнения следует, что z – любое число.
2. Однополостной гиперболоид обладает
центральной
симметрией относительно начала координат,осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Слайд 14Однополостный гиперболоид. Свойства
3. Если в уравнении однополостного гиперболоида a=b, то
сечения гиперболоида плоскостями, параллельными плоскости xOy, являются окружностями. В этом
случае поверхность называется однополостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости yOz, вокруг оси Oz.
Слайд 152.3. Гиперболоиды.
Двуполостный гиперболоид
Определение 3. Двуполостным гиперболоидом называется поверхность, каноническое
уравнение которой имеет вид
Слайд 16Двуполостный гиперболоид. Свойства
Свойства однополостного гиперболоида.
1. Двуполостный гиперболоид – неограниченная поверхность,
поскольку из его уравнения следует, что
и неограничен сверху.2. Двуполостный гиперболоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении двуполостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.
Слайд 17Двуполостный гиперболоид. Свойства
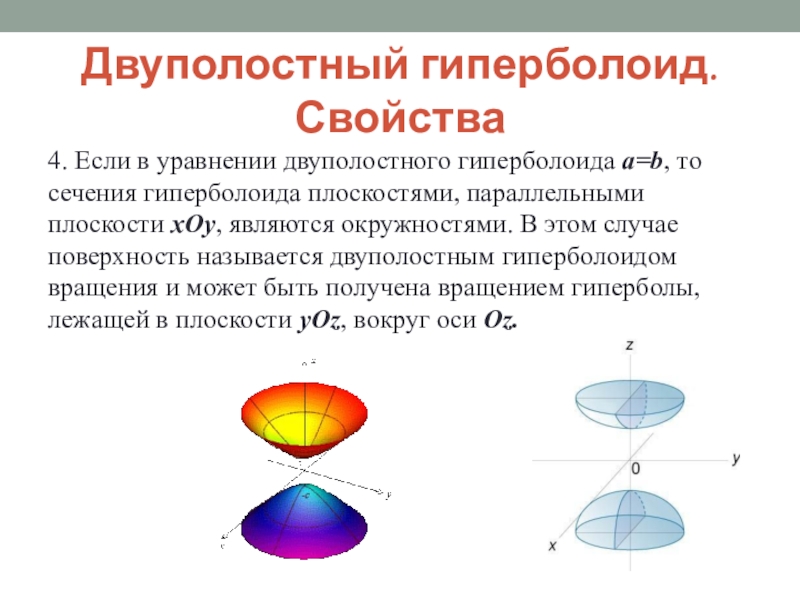
4. Если в уравнении двуполостного гиперболоида a=b, то
сечения гиперболоида плоскостями, параллельными плоскости xOy, являются окружностями. В этом
случае поверхность называется двуполостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости yOz, вокруг оси Oz.
Слайд 182.4. Конические поверхности (конус)
Определение 4.
Конусом второго порядка называется поверхность, уравнение
которой
в некоторой декартовой
системе координат
имеет вид:
Замечание 1.
С математической точки зрения коническую поверхность лучше определять с помощью уравнения
так как в нем меньше параметров, но при этом, теряется аналогия с уравнениями предыдущих поверхностей
Слайд 19Конус. Свойства
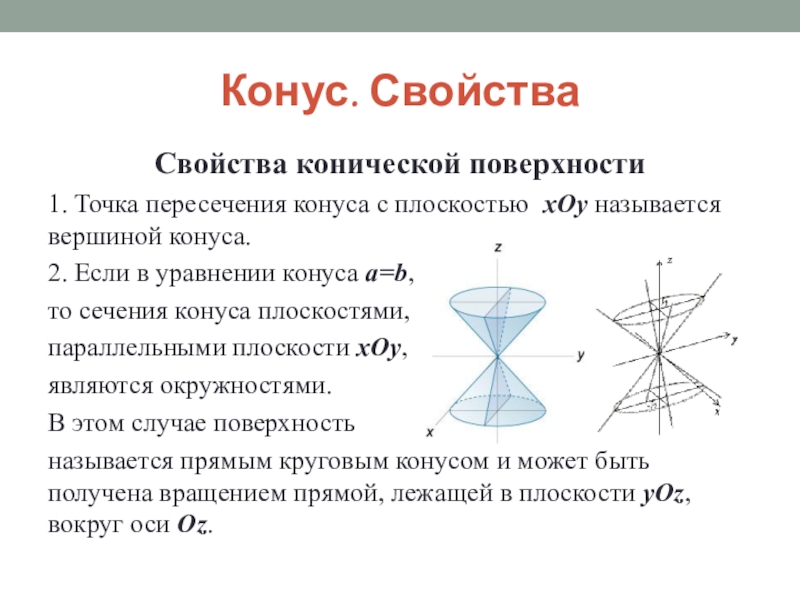
Свойства конической поверхности
1. Точка пересечения конуса с плоскостью xOy
называется вершиной конуса.
2. Если в уравнении конуса a=b,
то
сечения конуса плоскостями, параллельными плоскости xOy,
являются окружностями.
В этом случае поверхность
называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости yOz, вокруг оси Oz.
Слайд 212.5.1. Эллиптический параболоид
Определение 5.
Эллиптическим параболоидом называется поверхность, уравнение которой
в некоторой декартовой системе координат имеет вид:
Слайд 22Эллиптический параболоид. Свойства
Свойства эллиптического параболоида.
1. Эллиптический параболоид – неограниченная поверхность,
поскольку из его уравнения следует, что и
принимает сколь угодно большие значения.2. Эллиптический параболоид обладает:
осевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных осей Oxz и Oyz.
3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.
Слайд 23Эллиптический параболоид. Свойства
4. Вся поверхность может быть получена движением параболы,
лежащей в плоскости xOz. Парабола должна двигаться так, чтобы ее
плоскость была параллельна плоскости xOz, а вершина скользила по параболе в плоскости yOz.5. Если в уравнении поверхности a=b,
то сечения плоскостями,
параллельными плоскости xOy,
являются окружностями.
В этом случае поверхность называется
параболоидом вращения
и может быть образована вращением параболы, лежащей в плоскости yOz, вокруг оси Oz.
Слайд 242.5.2. Гиперболический параболоид
Определение 6.
Гиперболическим
параболоидом называется поверхность,
уравнение которой
в некоторой декартовой системе координат имеет вид:
Слайд 25Гиперболический параболоид. Свойства
Свойства гиперболического параболоида.
1. Гиперболический параболоид – неограниченная поверхность,
поскольку из его уравнения следует, что z – любое число.
2. Гиперболический параболоид
обладаетосевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.
3. В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox и Oy, – парабола.
4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
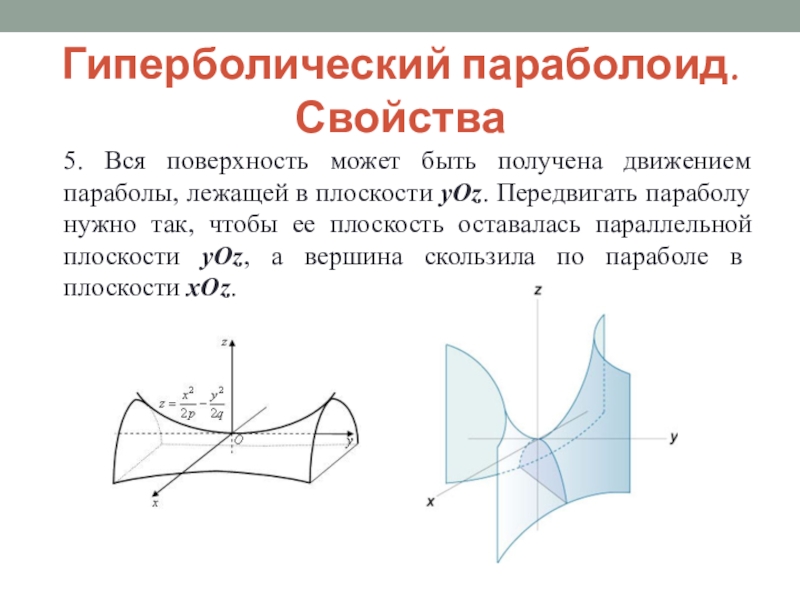
Слайд 26Гиперболический параболоид. Свойства
5. Вся поверхность может быть получена движением параболы,
лежащей в плоскости yOz. Передвигать параболу нужно так, чтобы ее
плоскость оставалась параллельной плоскости yOz, а вершина скользила по параболе в плоскости xOz.
Слайд 272.6. Цилиндрические поверхности
Определение 7.
Цилиндрической поверхностью называется геометрическое место параллельных
прямых, пересекающих данную линию.
Эта линия называется направляющей, а параллельные
прямые образующими. 
Слайд 332.8. Классификация поверхностей второго порядка
Исследование вида поверхности второго порядка может
быть проведено с помощью инвариантов поверхностей второго порядка, составленных из
коэффициентов уравнения (2.1). Основные инварианты:
Слайд 35Классификация поверхностей второго порядка. Основные инварианты
Непосредственной проверкой можно убедиться, что
их значения не меняются при параллельном переносе и повороте осей
координат. Семиинварианты (полуинварианты) ∆' и ∆'', которые являются инвариантами относительно поворота системы координат:где алгебраическое дополнение элемента в
Слайд 36Классификация поверхностей второго порядка. Основные инварианты
Поверхность второго порядка, заданная общим
уравнением (2.1), называется не вырождающейся , если ∆ ≠ 0,
и вырождающейся в случае если ∆ = 0.К не вырождающимся поверхностям относятся эллипсоид, однополостный и двуполостный гиперболоиды, гиперболический и эллиптические параболоиды. К вырождающимся поверхностям относятся цилиндрические поверхности.
Слайд 37Классификация поверхностей второго порядка Таблица 1. - Классификация поверхностей второго порядка
по инвариантам
Слайд 392.9. Поверхности второго порядка в сферических координатах
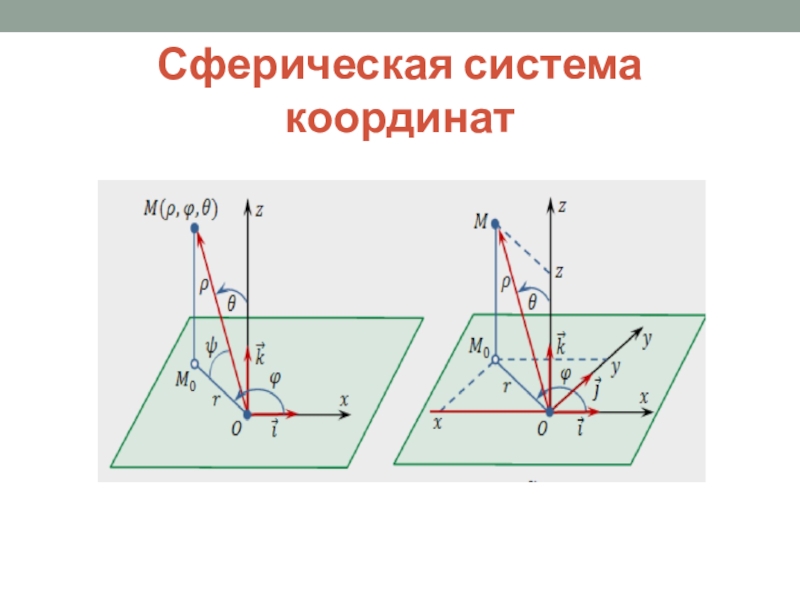
Для введения сферической системы
координат в пространстве выбирается плоскость (основная плоскость) и на ней
задается полярная система координат с полюсом O (начало сферической системы координат) и полярной осью Ox. Через точку O перпендикулярно основной плоскости проведем ось Oz (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси Oz происходило против часовой стрелки.
Слайд 43Сферическая система координат
Со сферической системой координат можно связать прямоугольную систему координат,
у которой начало и базисные векторы совпадают с началом сферической системы
координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат (связанную с данной прямоугольной).
Слайд 44Переход от сферических координат к декартовым координатам
Приведем формулы связывающие между
собой декартовы и сферические координаты:
Слайд 45Переход от сферических координат к декартовым координатам
Эти формулы перехода позволяют
найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется
по формулам
Слайд 49Пример 1. Решение
б) Найдем сферические координаты точки A(4;-3;12). Используя формулы
перехода из сферической системы координат в декартовую получим:
Слайд 50Пример 1. Решение
в) По формулам перехода из декартовой системы координат
в сферическую систему координат получим:
