Лекция 2. Проецирование плоскости

Содержание

1. Лекция 2. Проецирование плоскости
2. 1. Способы задания плоскостиа) тремя точками,
3. QХе) следами.След плоскости - это линия пересечения плоскости с плоскостью проекцийf2Qh1Qf2Qh1QKK1=K2
4. 2.1. Плоскость общего положенияАВСА2=А3В2=В1С1С3С2=А1=В3h1p3f2 2. Общее и частное положение плоскости в пространствеf2h1p3
5. Проецирующие плоскостиNm ХN2N1m2m1=h1βh12.2. Плоскости частного положенияа) Горизонтально-проецирующая,  П1f2β
6. б) Фронтально-проецирующая плоскость,  П2QαХQ2 =f2h1M2 = M1αQ2=f2h1M
7. в) Профильно-проецирующая,  П3Гmnn2Г3=р3=m3=n3n1m2m1ααββ
8. а) Горизонтальная плоскость уровня, ll П1Плоскости уровня
9. б) Фронтальная плоскость уровня, ll П2к1a1=с1к2с2п2п1а2
10. в) Профильная плоскость уровня, ll П3А3В3С3D3А2 = В2D2С2= А1= D1В1 = С1ФФ1Ф2
11. 3. Принадлежность точки и линии плоскостиА2Задано:Две проекции
12. 4. Главные линии плоскости: горизонталь и фронтальa1b1a2b211122221f2f1C1A1B1C2B2A21112h1h2
13. Линия наибольшего скатаdd1d2hd – линия наибольшего скатаa2b2a1b1h2h1d2d1
14. 5. Взаимное положение плоскостей Плоскости
15. Построение параллельной плоскостиК2К1h2h1f2f1M2M1h¹2h¹1f¹1f¹2h2 // h¹2 ,
16. Изображение пересекающихся плоскостейQΔMN
17. Построение перпендикулярной плоскостиΔАhfnQQ( n  h
18. Желаю здравствовать!Читайте литературу!Не пренебрегайте самостоятельной работой!
19. Скачать презентанцию

1. Способы задания плоскостиа) тремя точками, б) точкой и прямой, в) параллельными прямыми, г) пересекающимися прямыми, д) плоской фигуройА2А1В2В1С2С1М2М1f1f2m2n2m1n1K2K1e2e1

Главная
Разное
Лекция 2. Проецирование плоскости

Слайды и текст этой презентации

Слайд 11. Способы задания плоскости.
2. Общее и частное положение плоскости в

пространстве.
3. Принадлежность точки и линии плоскости.
4. Главные линии плоскости.
5.

Взаимное положение плоскостей.

Лекция 2. Проецирование плоскости

1. Способы задания плоскости.2. Общее и частное положение плоскости в пространстве. 3. Принадлежность точки и линии плоскости.4.

Слайд 2 1. Способы задания плоскости
а) тремя точками, б) точкой и

прямой, в) параллельными прямыми, г) пересекающимися прямыми, д) плоской фигурой
А2
А1
В2
В1
С2
С1
М2
М1
f1
f2
m2
n2
m1
n1
K2
K1
e2
e1

1. Способы задания плоскостиа) тремя точками, б) точкой и прямой, в) параллельными прямыми, г) пересекающимися прямыми,

Слайд 3Q
Х
е) следами.
След плоскости - это линия пересечения плоскости с плоскостью

проекций
f2Q
h1Q
f2Q
h1Q
K
K1=K2

Слайд 42.1. Плоскость общего положения

А
В
С
А2=А3
В2=В1
С1
С3
С2=А1=В3
h1
p3
f2
2. Общее и частное положение плоскости

в пространстве
f2
h1
p3

Слайд 5Проецирующие плоскости
N
m

Х
N2
N1
m2
m1=h1
β
h1
2.2. Плоскости частного положения
а) Горизонтально-проецирующая,  П1
f2
β

Слайд 6 б) Фронтально-проецирующая плоскость,  П2
Q
α
Х
Q2 =f2
h1
M2 = M1
α
Q2=f2
h1
M

Слайд 7в) Профильно-проецирующая,  П3
Г
m
n
n2
Г3=р3=m3=n3
n1
m2
m1
α
α
β
β

Слайд 8а) Горизонтальная плоскость уровня, ll П1
Плоскости уровня

Слайд 9б) Фронтальная плоскость уровня, ll П2
к1
a1=с1
к2
с2
п2
п1
а2

Слайд 10в) Профильная плоскость уровня, ll П3
А3
В3
С3
D3
А2 = В2
D2
С2= А1= D1
В1

= С1
Ф
Ф1
Ф2

Слайд 113. Принадлежность точки и линии плоскости
А2
Задано:
Две проекции четырехугольника.
Фронтальная проекция

А2 точки А, принадлежащей EFKD
Решение:
Проводим через A2 прямую m2 ll

E2F2;
Находим точку 12 XE2D2;
Строим 11XE1D1;
Проводим m1 ll E1F1;
Строим по линии связи А1 Xm1.

Е2

Е1

А1

Найти:
положение горизонтальной проекции А1 точки А

3. Принадлежность точки и линии плоскостиА2Задано:Две проекции четырехугольника. Фронтальная проекция А2 точки А, принадлежащей EFKDРешение:Проводим через A2

Слайд 124. Главные линии плоскости: горизонталь и фронталь
a1
b1
a2
b2
11
12
22
21
f2
f1
C1
A1
B1
C2
B2
A2
11
12
h1
h2

Слайд 13Линия наибольшего ската
d
d1
d2
h
d – линия наибольшего ската
a2
b2
a1
b1
h2
h1
d2
d1

Слайд 145. Взаимное положение плоскостей
Плоскости в пространстве могут

быть параллельны или пересекаться.
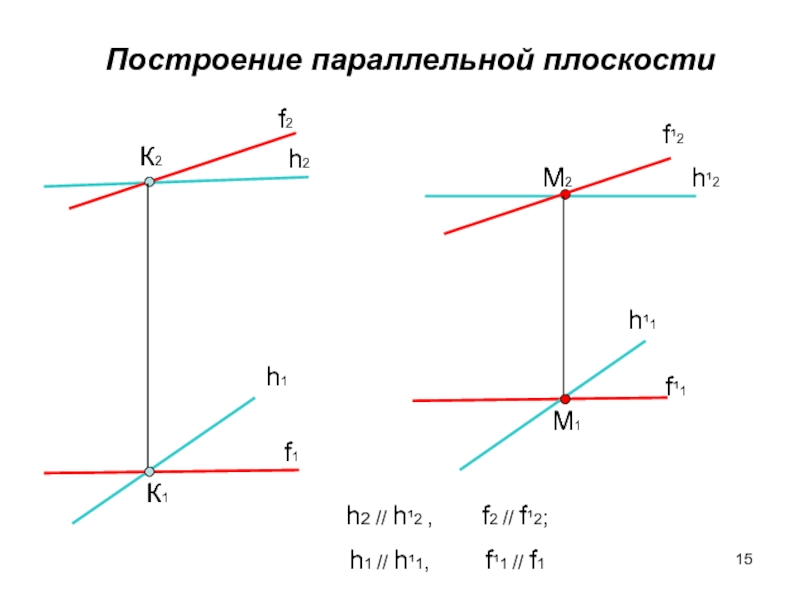
1. Параллельность плоскостей. Для параллельности плоскостей достаточно,

чтобы две пересекающиеся прямые одной плоскости были параллельны двум пересекающимся прямым другой плоскости.

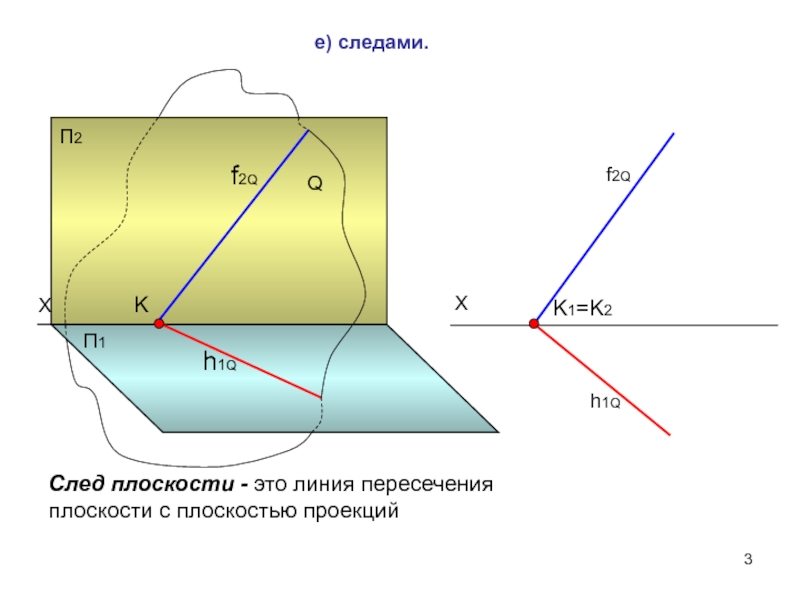
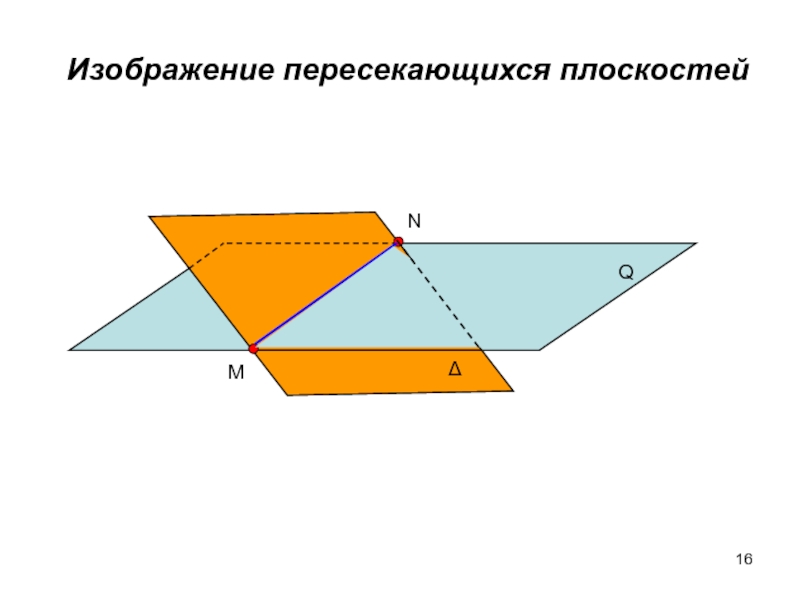
2. Пересечение плоскостей. Результатом пересечения двух плоскостей является прямая линия, для построения которой достаточно найти две точки, общие для пересекающихся плоскостей.

3. Перпендикулярность плоскостей. Две плоскости взаимно перпендикулярны, если одна из них содержит перпендикуляр к другой. Прямая, перпендикулярная плоскости, называется нормалью плоскости и перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

5. Взаимное положение плоскостей Плоскости в пространстве могут быть параллельны или пересекаться.1. Параллельность плоскостей. Для

Слайд 15 Построение параллельной плоскости
К2
К1
h2
h1
f2
f1
M2
M1
h¹2
h¹1
f¹1
f¹2
h2 // h¹2 ,

f2 // f¹2;
h1 // h¹1, f¹1

// f1

Построение параллельной плоскостиК2К1h2h1f2f1M2M1h¹2h¹1f¹1f¹2h2 // h¹2 , f2 // f¹2;h1 // h¹1,

Слайд 16 Изображение пересекающихся плоскостей
Q
Δ
M
N

Слайд 17 Построение перпендикулярной плоскости
Δ
А
h
f
n
Q
Q( n  h ∩ n 

f, m )  Δ( h ∩ f)
A1
f1
h2
h1
A2
f2
n1
n2
m
K
m2
m1
K2
K1

Построение перпендикулярной плоскостиΔАhfnQQ( n  h ∩ n  f, m )  Δ( h ∩

Слайд 18Желаю здравствовать!

Читайте литературу!

Не пренебрегайте самостоятельной работой!

Скачать презентацию

Разделы презентаций

Лекция 2. Проецирование плоскости

Содержание

Слайды и текст этой презентации

Слайд 11. Способы задания плоскости.
2. Общее и частное положение плоскости в

пространстве.
3. Принадлежность точки и линии плоскости.
4. Главные линии плоскости.
5.

Слайд 2 1. Способы задания плоскости
а) тремя точками, б) точкой и

прямой, в) параллельными прямыми, г) пересекающимися прямыми, д) плоской фигурой
А2
А1
В2
В1
С2
С1
М2
М1
f1
f2
m2
n2
m1
n1
K2
K1
e2
e1