Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 2 Тема : Временное и спектральное представление детерминированных
Содержание
- 1. Лекция 2 Тема : Временное и спектральное представление детерминированных
- 2. 1-й вопрос: Основные понятия о детерминированных сигналахПонятие детерминированного сигнала.Случайный сигнал.
- 3. Понятие детерминированного сигналаДетерминированным называется сигнал, который точно
- 4. Случайный сигналСлучайным сигналом называют функцию времени, значения
- 5. 2-й вопрос: Характеристики и закономерности дискретных сигналовПринципы
- 6. Принципы формирования дискретных сигналовЛюбой дискретный сигнал чаще
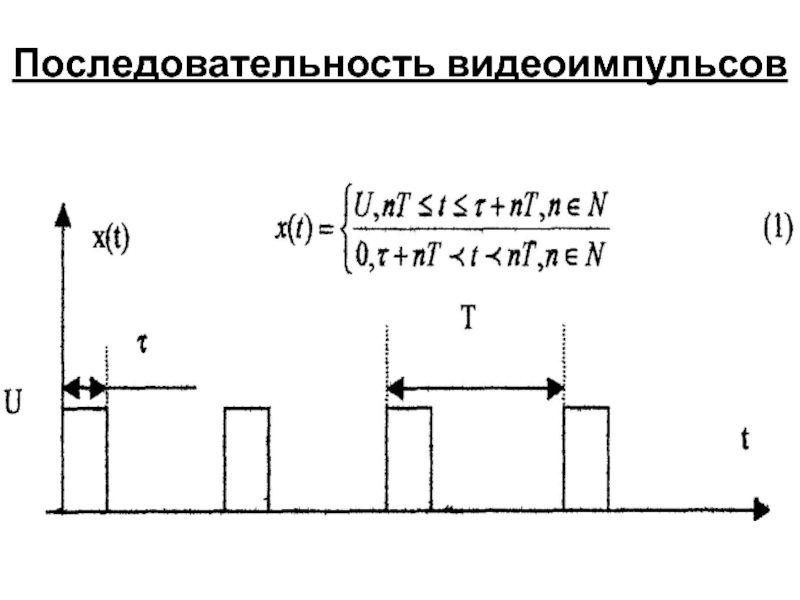
- 7. Последовательность видеоимпульсов
- 8. Скважность импульсной последовательности Отношение называется скважностью импульсной
- 9. Временные характеристики дискретных сигналов1. Длительность импульса τ.2.
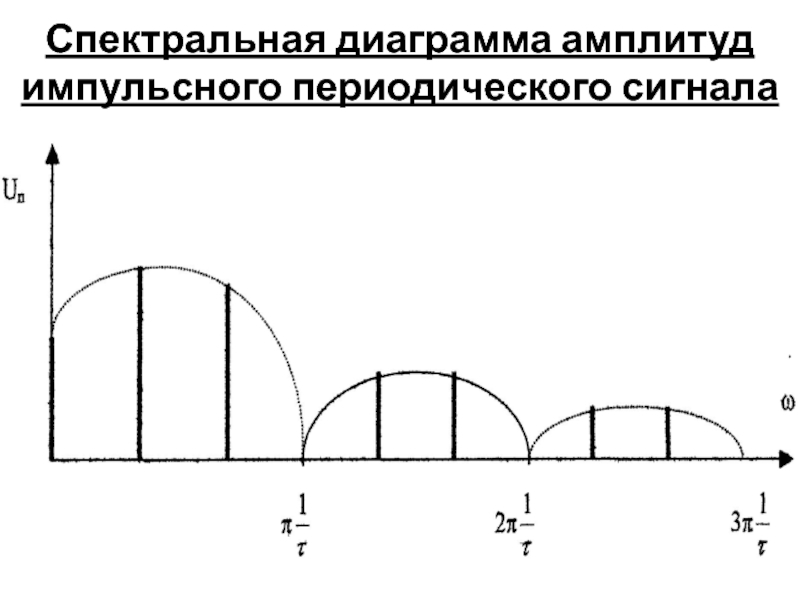
- 10. Спектральная диаграмма амплитуд импульсного периодического сигнала
- 11. Спектр амплитуд и фаз сигналаСовокупность амплитуд составляющих
- 12. Спектральные характеристики ИДС1. Основная частота «телеграфирования» -
- 13. Связь спектра ИПС и полосы пропускания КСЧастотный
- 14. Закономерности спектра дискретных сигналов 1. Частотный спектр
- 15. Скорость передачи ДСПод технической скоростью передачи дискретных
- 16. Многозначное кодирование При использовании многозначного коди- рования, значение
- 17. Минимальная полоса пропусканияСуществует зависимость между скоростью передачи
- 18. Предел НайквистаИз ТЭРЦ известно, что минимальная длительность
- 19. Свойства преобразования Фурье а) Сдвиг сигнала
- 20. Скачать презентанцию
1-й вопрос: Основные понятия о детерминированных сигналахПонятие детерминированного сигнала.Случайный сигнал.
Слайды и текст этой презентации
Слайд 1Лекция 2
Тема: Временное и спектральное представление детерминированных сигналов
Учебные вопросы:
1. Основные
понятия о детерминированных сигналах.
непериодических сигналов.Слайд 21-й вопрос: Основные понятия о детерминированных сигналах
Понятие детерминированного сигнала.
Случайный сигнал.
Слайд 3Понятие детерминированного сигнала
Детерминированным называется сигнал, который точно определен в любой
момент времени (например, задан в аналитическом виде). Детерминированные сигналы могут
быть периодическими и непериодическими.Периодическим называется сигнал, для которого выполняется условие s(t) = s(t + кT), где к - любое целое число, Т - период, являющийся конечным отрезком времени.
Любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте
Непериодический сигнал, как правило, ограничен во времени.
Слайд 4Случайный сигнал
Случайным сигналом называют функцию времени, значения которой заранее неизвестны
и могут быть предсказаны лишь с некоторой вероятностью. В качестве
основных характеристик случайных сигналов принимают:а) закон распределения вероятности (относительное время пребывания величины сигнала в определенном интервале);
б) спектральное распределение мощности сигнала.
Слайд 52-й вопрос: Характеристики и закономерности дискретных сигналов
Принципы формирования дискретных сигналов.
Последовательность
видеоимпульсов.
Скважность импульсной последовательности.
Временные характеристики дискретных сигналов.
Спектральная диаграмма амплитуд импульсного периодического
сигнала (ИПС).Спектральные характеристики ИПС.
Связь спектра ИПС и полосы пропускания канала связи (КС).
Закономерности спектра дискретных сигналов (ДС).
Скорость передачи ДС.
Многозначное кодирование.
Минимальная полоса пропускания.
Предел Найквиста.
Слайд 6Принципы формирования дискретных сигналов
Любой дискретный сигнал чаще формируется на основе
двоичной сис- темы счисления, хотя известны случаи использования многозначной системы
счисления. Это определяет число отличительных признаков элементарных импульсов, в данном случае – 2.При формировании первичных дискретных сигналов (видеосигналы или сигналы низкой частоты) чаще всего используют амплитудный или полярный отличительные признаки. Если они передаются по радиоканалам или по проводным каналам с использованием аппара- туры тонального телеграфирования, то применяют модуляцию несущего ВЧ колебания данными первичными дискретными сигнала- ми. При этом используются амплитудный, частотный, фазовый призна- ки (сигналы А1, А2, F1, F2, F6, F9). При формировании дискретных сиг- налов в ряде цифровых систем передачи, модуляция несущего колеба- ния не используется – происходит передача в основной полосе частот, хотя и с применением специальных преобразований (преобразования к коду передачи). В этом случае чаще всего используется полярный отличительный признак.
Слайд 8Скважность импульсной последовательности
Отношение называется скважностью импульсной последовательности. Импульсная последовательность
сигналов со скважностью равной 2 называется меандром и играет важную
роль в технике связи. Такие сигналы используются при проверках, при вхождении в синхронизм, при анализе систем связи и их элементов.Слайд 9Временные характеристики дискретных сигналов
1. Длительность импульса τ.
2. Период последовательности импульсов
Т;
3. Скважность импульсной последовательности q.
4. Это характеристики идеальных дискретных сигналов.
Реальные дискретные сигналы имеют конечную длительность переднего τпф и заднего τзф фронтов, которые также используются при их описании.Слайд 11Спектр амплитуд и фаз сигнала
Совокупность амплитуд составляющих спектральную диаграмму амплитуд
сигнала называют спектром амплитуд сигнала.
Фазовым спектром называют совокупность начальных фаз
ψn сигнала. Амплитудный и фазовый спектры полностью определяют дискретный сигнал в частотной области.Слайд 12Спектральные характеристики ИДС
1. Основная частота «телеграфирования» - это частота первой
гармоники сигнала
2. Величина постоянной составляющей
3. Величина или ширина
первого лепестка огибающей амплитудного спектра 4. Число дискретных гармонических составляющих в первом лепестке огибающей, которое равно q –1.
Слайд 13Связь спектра ИПС и полосы пропускания КС
Частотный спектр дискретного сигнала
бесконечен. Следовательно, для неискаженной передачи такого сигнала требуется линия или
канал связи с бесконечно широкой полосой пропускания, в то время как реальные системы связи имеют полосы пропускания, ширина которых ограничена. Это противоречие разрешается достаточно просто, если иметь в виду, что нет необходимости передавать по линии связи импульсы идеальной формы. В дискретных двоичных каналах достаточно зафиксировать факт наличия или отсутствия импульса. А это, в свою очередь, позволяет организовать связь в линиях и каналах связи с конечной полосой пропускания.Теоретические и экспериментальные исследования показали, что для надёжной регистрации дискретного сигнала достаточна полоса пропускания канала с верхней граничной полосой .
В такой полосе сосредоточено до 88 % энергии сигнала. Такую полосу частот, занимаемую спектром сигнала, называют эффективной полосой.
Слайд 14Закономерности спектра дискретных сигналов
1. Частотный спектр дискретных сигналов бесконечен,
однако основная доля мощности спектральных составляющих дискретных сигналов лежит в
эффективной полосе и может достигать 88 %.2. Огибающая амплитуд спектра носит лепестковый характер, лепестки спектра ограничиваются частотами, кратными 1/τ.
3. Амплитуды спектральных составляющих с увеличением номера гармоники уменьшаются, постоянная составляющая равна .
4. Частоты спектральных составляющих кратны основной частоте повторения импульсов f1=1/T, причём в основной полосе от нуля до 1/τ располагаются q-1 гармоник.
Слайд 15Скорость передачи ДС
Под технической скоростью передачи дискретных сигналов понимают количество
элементарных символов, передаваемых в одну секунду. В телеграфии используется синонимичный
термин – скорость телеграфирования.Единицей измерения технической скорости передачи является Бод. Одному Боду соответствует скорость передачи, при которой в 1 сек передается 1 импульс:
Информационная скорость измеряется в бит/сек и численно равна количеству единиц информации, передаваемых в секунду.
При передаче дискретных сигналов двоичным безизбыточным кодом техническая и информационная скорости численно равны.
Слайд 16Многозначное кодирование
При использовании многозначного коди- рования, значение информационной ско- рости
вырастает в log 2 m раз, где m – основание
системы счисления. Кроме того, при использовании помехоустойчивого избыточного кодирования передаваемых сообщений информационная скорость в двоичном канале меньше технической скорости.Слайд 17Минимальная полоса пропускания
Существует зависимость между скоростью передачи дискретных сигналов и
шириной полосы пропускания используемого канала связи.
Самым информативным дискретным сигналом является
сигнал со скважностью 2, поскольку за период передается два технических импульса и дальнейшее увеличение информативности возможно только за счёт уменьшения длительности импульса. Это же приведет к увеличению ширины полосы спектра сигнала, которая фиксирована в наших рассуждениях полосой пропускания канала. При этом минимальная полоса пропускания для такого сигнала будет . В этом случае в полосу пропускания канала попадают постоянная составляющая и первая гармоника.
Слайд 18Предел Найквиста
Из ТЭРЦ известно, что минимальная длительность импульса численно равна
длительности переднего (или заднего) фронта. А величина переднего фронта определяется
половиной периода максимальной частоты в спектре сигнала. ТогдаВ этом случае по определению
Это выражение известно как предел Найквиста и которое устанавливает предельное значение дости- жимой скорости передачи дискретных сигналов по двоичному каналу связи с максимальным значе- нием верхней граничной частоты его полосы про- пускания Fmax.
Слайд 19
Свойства преобразования Фурье
а) Сдвиг сигнала во времени s2(t)=s1(t-t0).
б) Сжатие и
расширение сигнала s2(t)=s1(nt).
При сжатии сигнала в n раз на временной
оси во столько же раз расширяется его спектр на оси частот при уменьшении модуля в n раз. Наоборот, при растяжении сигнала во времени имеет место сужение спектра и увеличение модуля спектральной плотности. Т. о. сжатие спектра импульса с целью повышения точности измерения частоты требует удлинения времени измерения. В то же время сжатие импульса по времени с целью, например, повышения точности измерения времени его появления заставляет расширять полосу пропускания измерительного устройства. в) Дифференцирование и интегрирование сигнала
г) Сложение сигналов (линейность преобразования)
д) Спектр произведения двух функций равен свертке их спектров.
е) Взаимная обратимость.