Слайд 1Лекция 20
Тема 2.2. Растяжение и сжатие. Внутренние силовые факторы, напряжения.
Построение эпюр
Иметь представление о продольных силах, о нормальных напряжениях в
поперечных сечениях.
Знать правила построения эпюр продольных сил и нормальных напряжений, закон распределения нормальных напряжений в поперечном сечении бруса.
Уметь строить эпюры продольных сил и нормальных напряжений.
Растяжение и сжатие
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. 20.1б).
Слайд 2Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними
силами вдоль
оси. Брус закреплен в стене
(закрепление «заделка») (рис. 20.2а).
Делим
брус на участки нагружения.
Участком нагружения считают часть бруса между
внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим
внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы
не определять величины реакций в опорах.
Продольная сила положительна, участок 1 растянут.
Продольная сила положительна, участок 2 растянут.
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы
(рис. 20.2, б).
Эпюрой продольной силы называется график
распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Слайд 3Правило контроля: в месте приложения внешней силы на эпюре должен
быть скачок на величину приложенной силы.
На эпюре проставляются значения Nz.
Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
где Nz — продольная сила в сечении; А — площадь поперечного сечения.

Слайд 4Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади
поперечного сечения.
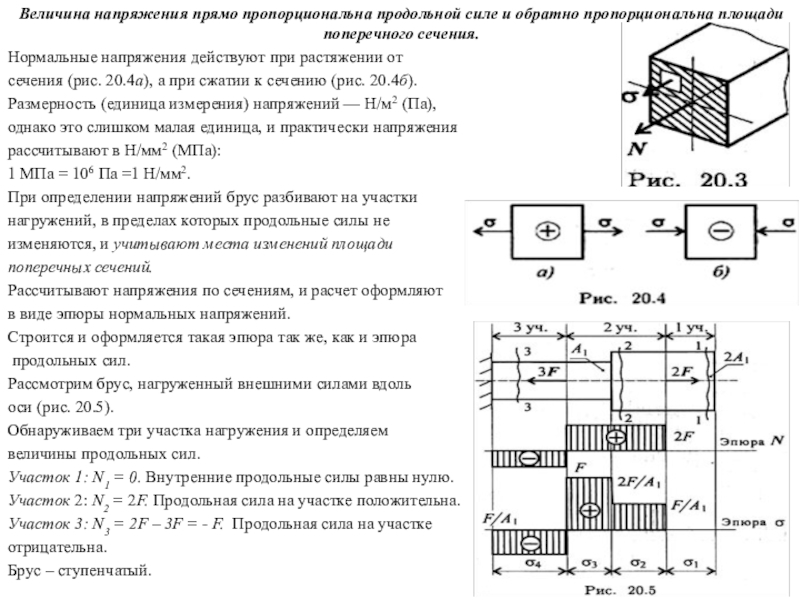
Нормальные напряжения действуют при растяжении от
сечения (рис. 20.4а),
а при сжатии к сечению (рис. 20.4б).
Размерность (единица измерения) напряжений — Н/м2 (Па),
однако это слишком малая единица, и практически напряжения
рассчитывают в Н/мм2 (МПа):
1 МПа = 106 Па =1 Н/мм2.
При определении напряжений брус разбивают на участки
нагружений, в пределах которых продольные силы не
изменяются, и учитывают места изменений площади
поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют
в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра
продольных сил.
Рассмотрим брус, нагруженный внешними силами вдоль
оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем
величины продольных сил.
Участок 1: N1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N2 = 2F. Продольная сила на участке положительна.
Участок 3: N3 = 2F – 3F = - F. Продольная сила на участке
отрицательна.
Брус – ступенчатый.
Слайд 5С учетом изменений величин площади поперечного сечения участков напряжений больше.
Строим
эпюры продольных сил и нормальных напряжений.
Масштабы эпюр могут быть разными
и выбираются исходя из удобства построения.
Примеры решения задач
Пример 1. Ступенчатый брус нагружен вдоль оси двумя силами.
Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом
бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
Определяем участки нагружения, их два.
Определяем продольную силу в сечениях 1 и 2.
Строим эпюру.
Рассчитываем величины нормальных напряжений и строим эпюру
нормальных напряжений в собственном произвольном масштабе.
1.Определяем продольные силы.
В обоих сечениях продольные силы положительны.
Слайд 62.Определяем нормальные напряжения
Сопоставляя участки нагружения с границами изменения площади, видим,
что образуется 4 участка напряжений.
Нормальные напряжения в сечениях по участкам:
Откладываем
значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Слайд 7Пример 2. Для заданного бруса (рис. 2.5, а) построить эпюры
продольных сил и нормальных напряжений.
Решение
Заданный брус имеет четыре участка I,
II, III, IV (рис. 2.5, а).
Границами участков являются сечения, в которых приложены
внешние силы, а для напряжений также и места изменения
размеров поперечного сечения.
Пользуясь методом сечений, строим эпюру продольных сил
(рис. 2.5, б).
Для построения эпюры нормальных напряжений определяем
их в поперечных сечениях каждого из участков:
Эпюра σ представлена на рис. 2.5, в.
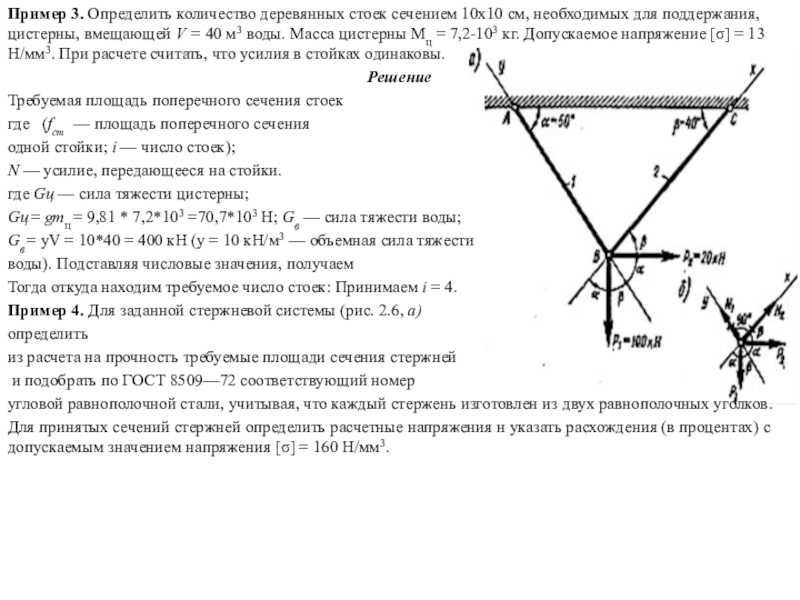
Слайд 8Пример 3. Определить количество деревянных стоек сечением 10x10 см, необходимых
для поддержания, цистерны, вмещающей V = 40 м3 воды. Масса
цистерны Мц = 7,2-103 кг. Допускаемое напряжение [σ] = 13 Н/мм3. При расчете считать, что усилия в стойках одинаковы.
Решение
Требуемая площадь поперечного сечения стоек
где (fст — площадь поперечного сечения
одной стойки; i — число стоек);
N — усилие, передающееся на стойки.
где Gц — сила тяжести цистерны;
Gц = gтц = 9,81 * 7,2*103 =70,7*103 Н; Gв — сила тяжести воды;
Gв = уV = 10*40 = 400 кН (у = 10 кН/м3 — объемная сила тяжести
воды). Подставляя числовые значения, получаем
Тогда откуда находим требуемое число стоек: Принимаем i = 4.
Пример 4. Для заданной стержневой системы (рис. 2.6, а)
определить
из расчета на прочность требуемые площади сечения стержней
и подобрать по ГОСТ 8509—72 соответствующий номер
угловой равнополочной стали, учитывая, что каждый стержень изготовлен из двух равнополочных уголков.
Для принятых сечений стержней определить расчетные напряжения н указать расхождения (в процентах) с допускаемым значением напряжения [σ] = 160 Н/мм3.
Слайд 9Решение
Здесь требуется подобрать сечения стержней исходя из условий:
где N1 и
N2 — усилия, возникающие соответственно в стержнях 1 и 2.
Усилия
N1 и N2 во всех поперечных сечениях стержней одинаковы и площади этих сечений постоянны. Таким образом, все сечения каждого стержня равноопасны.
Определяем усилия в стержнях из рассмотрения равновесия узла В, где приложены заданные силы Р1 и Р2 (рис. 2.6, б). Освобождаем эту точку от связей и прикладываем их реакции N1 и N2, равные усилиям в стержнях. Получаем плоскую систему сходящихся сил. Для упрощения уравнений равновесия координатные оси ху направляем вдоль неизвестных усилий N1 и N2. Составляем уравнения равновесия:
Откуда
Тогда
Слайд 10По таблицам ГОСТ 8509—72 подбираем сечения стержней:
для первого стержня угловую
равнополочную сталь 36x36x4
для второго стержня угловую равнополочную сталь 28x28x3
Вычислим напряжения
в поперечных сечениях стержней при принятых площадях
что больше [σ] на
такое превышение допустимо;
что меньше [σ] на
Слайд 11Пример 5. Определить размеры поперечных сечений стержней
(рис. 2.7, а),
если допускаемые напряжения для
стали [σсх] = 140 Н/мм2,для дерева
[σд] = 13 Н/мм2.
Решение
Рассматриваем равновесие шарнира А, так как
к этому шарниру
приложены заданная нагрузка и искомые усилия в стержнях.
Освобождаем шарнир А от связей и заменяем
их действие реакциями N1 и N2. Действующие на
шарнир А нагрузка и искомые усилия показаны
на рис. 2.7, б. Получили плоскую
систему сходящихся сил, которая находится в равновесии.
Выбираем систему координат и составляем уравнения равновесия:
откуда
Слайд 12Требуемые площади поперечных сечений стержней
Откуда
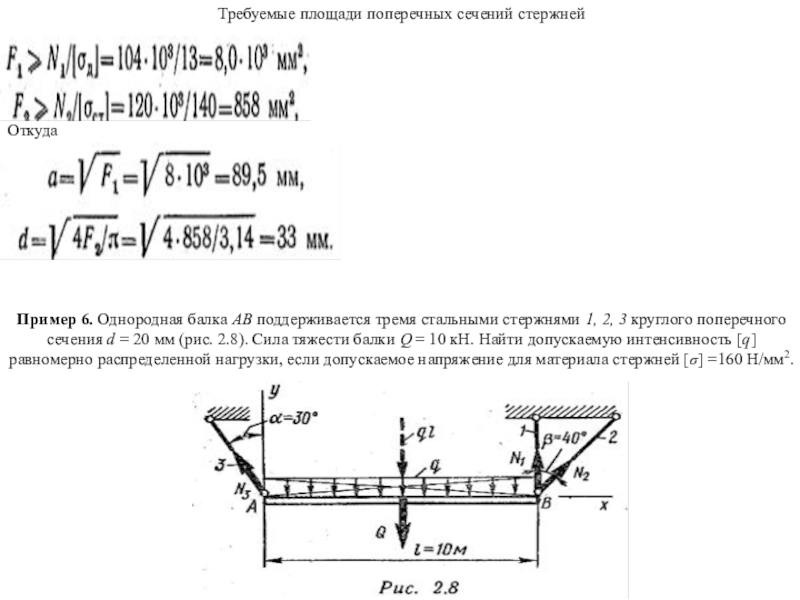
Пример 6. Однородная балка АВ поддерживается
тремя стальными стержнями 1, 2, 3 круглого поперечного сечения d
= 20 мм (рис. 2.8). Сила тяжести балки Q = 10 кН. Найти допускаемую интенсивность [q] равномерно распределенной нагрузки, если допускаемое напряжение для материала стержней [σ] =160 Н/мм2.
Слайд 13Решение
1.Определим усилия, возникающие в стержнях. Под действием силы Q, равномерно
распределенной нагрузки q и усилий N1, N2 и N3 в
стержнях балка находится в равновесии.
2.Составляем уравнения равновесия:
3.Решая полученные уравнения, находим:
N3 больше, чем N1 и N2. Следовательно, опасными являются поперечные сечения стержня 3.
4.Условие прочности для стержня 3:
Подставляем значение N3:
5.Решая относительно ц и подставляя числовые значения, получаем:
где
Слайд 14Пример 7. Стальной стержень круглого сечения диаметром d = 20
мм растягивается силой Р = 65 кН.
Проверить прочность стержня,
если его предел текучести σ = σт = 300 Н/мм2 и требуемый коэффициент запаса [n] = 1,5.
Решение
Напряжения, возникающие в поперечном сечении стержня,
Расчетный коэффициент запаса
Следовательно, можно считать, что прочность стержня достаточна, так как расчетный коэффициент запаса незначительно (на 3%) меньше требуемого.
Слайд 15Контрольные вопросы и задания
1.Какие внутренние силовые факторы возникают в сечении
бруса при растяжении и сжатии?
2.Как распределяются по сечению силы упругости
при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
3.Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
4.Как распределены напряжения по сечению при растяжении и сжатии?
5.Запишите формулу для расчета нормальных напряжений при растяжении и сжатии.
6.Как назначаются знаки продольной силы и нормального напряжения?
7.Что показывает эпюра продольной силы?
8.Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
9.В каких единицах измеряется напряжение?









![Лекция 20 Тема 2.2. Растяжение и сжатие. Внутренние силовые факторы, Пример 5. Определить размеры поперечных сечений стержней (рис. 2.7, а), если Пример 5. Определить размеры поперечных сечений стержней (рис. 2.7, а), если допускаемые напряжения для стали [σсх] =](/img/thumbs/5b1093b977f0d0d62b72db7f822fdbc4-800x.jpg)